【电路理论五】频率特性和谐振现象

芳菲菲其弥章

已于 2024-12-30 21:40:47 修改

阅读量456

点赞数 10

分类专栏：电子技术基础文章标签：单片机

于 2024-12-29 16:11:54 首次发布

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.youkuaiyun.com/2301_79853895/article/details/144805507

版权

电子技术基础专栏收录该内容

12 篇文章

订阅专栏

网络函数和频率特性

网络函数的定义：

电路在单一激励作用下，响应相量与激励相量之比称为网络函数，即：

$H(j\omega)=\frac{\dot{Y}}{\dot{X}}$

网络函数分量：

（1）激励和响应属于同一端口

（2）激励和响应属于不同端口

对于幅频特性，其中RC具有时间的量纲，设

$\omega_0=\frac{1}{RC}$

称其为RC电路的固有频率或自然频率

代入可得：

RLC串联电路的频率特性

而对于RLC串联电路来说，以R为响应，频率特性如下：

$H_R(j\omega)=\frac{\dot{U_R}}{\dot{U}}=\frac{R}{R+j[\omega L-1/(\omega C)]}$

谐振角频率为

$\omega_0=\frac{1}{\sqrt{LC}}$

特性阻抗为：

$\rho =\omega_0L=1/\omega_0C=\sqrt{\frac{L}{C}}$

品质因数为：

$Q=\frac{\rho}{R}=\frac{1}{R}\sqrt{\frac{L}{C}}$

或为

$Q=\frac{\omega_0 L}{R}=\frac{1}{R\omega_0 C}$

将谐振角频率和品质因数代入上面的式子，写出幅频特性以及相频特性。

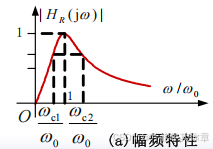
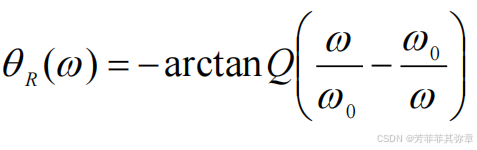
上面的 $\omega_{C1}$ 和 $\omega_{C2}$ 是得到的两个截止角频率，其中：

这说明带宽 $\Delta \omega$ 与品质因数 Q 成反比，Q 越大， $\Delta \omega$ 越小，通带越窄，曲线越尖锐，对信号的选择性越好。

如果以电容为响应，改变同理

如果以电感为响应，改变如下

串联谐振电路

对于含有电感和电容的一端口电路，如果在一定条件下呈现电阻性，即端口电压与电流同相位，则称此一端口电路发生谐振。

对于RLC串联谐振电路，发生谐振的条件为：

$\omega L=1/\omega C$

以下总结了串联谐振的特点：

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。