1018 锤子剪刀布

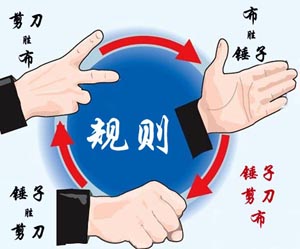
大家应该都会玩“锤子剪刀布”的游戏：两人同时给出手势，胜负规则如图所示：

现给出两人的交锋记录，请统计双方的胜、平、负次数，并且给出双方分别出什么手势的胜算最大。

输入格式：

输入第 1 行给出正整数 N（≤105），即双方交锋的次数。随后 N 行，每行给出一次交锋的信息，即甲、乙双方同时给出的的手势。C 代表“锤子”、J 代表“剪刀”、B 代表“布”，第 1 个字母代表甲方，第 2 个代表乙方，中间有 1 个空格。

输出格式：

输出第 1、2 行分别给出甲、乙的胜、平、负次数，数字间以 1 个空格分隔。第 3 行给出两个字母，分别代表甲、乙获胜次数最多的手势，中间有 1 个空格。如果解不唯一，则输出按字母序最小的解。

输入样例：

10
C J
J B
C B
B B
B C
C C
C B
J B
B C
J J

输出样例：

5 3 2
2 3 5
B B

 代码如下：

#include<iostream>
using namespace std;
int main()
{
    int n,i,k,a,b,ping=0,yinga=0,yingb=0;
    int na[3]={0},nb[3]={0};
    char ca,cb;
    cin>>n;   //输入石头剪刀布的局数n
    while(n--){
        cin>>ca>>cb;  //ca代表甲的手势，cb代表乙的手势
        if(ca=='B') a=0;  //根据甲的手势分别对a进行赋值
        else if(ca=='C') a=1;
        else if(ca=='J') a=2;
        if(cb=='B') b=0;  //根据乙的手势分别对b进行赋值
        else if(cb=='C') b=1;
        else if(cb=='J') b=2;
        if(a==b) ++ping;  //ping记录甲乙平局的局数
        else if(a==(b+1)%3) {  //一个方法，a如果等于(b+1)除以3取模，那这局就是乙赢
            ++nb[b];  //用数组nb在[0~2]的范围上存储相应手势下乙赢的次数
            ++yingb;  //统计乙赢了几局
        }
        else {  //不然就是甲赢。读者可将9种可能的情况列完后，自己探究~
            ++na[a];  //用数组na在[0~2]的范围上存储相应手势下甲赢的次数
            ++yinga;  //统计甲赢了几局
        }
    }
    cout<<yinga<<" "<<ping<<" "<<yingb<<endl;  //输出甲、乙的胜、平、负次数
    cout<<yingb<<" "<<ping<<" "<<yinga<<endl;
    for(i=0,k=0;i<3;i++){  //找到甲对局中获胜次数最多的手势，并用k间接记录该手势
        if(na[k]<=na[i]) k=i;  
    }
    for(i=0;i<3;i++){  //防止出现解不唯一(既有多个手势获胜次数一样多)
        if(i==k) continue;
        else if(na[i]==na[k]&&k>i) k=i;  //如果出现解不唯一,k间接存储相应字母序最小的那个
        }
    if(k==0) cout<<"B ";  //输出甲获胜次数最多的手势
    else if(k==1) cout<<"C ";
    else cout<<"J ";
    for(i=0,k=0;i<3;i++){  //对乙做同样的操作，不做过多赘述
    if(nb[k]<=nb[i]) k=i;
    }
        for(i=0;i<3;i++){
        if(i==k) continue;
        else if(nb[i]==nb[k]&&k>i) k=i;
        }
    if(k==0) cout<<"B";
    else if(k==1) cout<<"C";
    else cout<<"J";
    return 0;
}