今天在matrix平台上做题的时候遇到了一个题,如下


当然这个问题本身并不难,但因为我是按照今天数据结构课讲的初始化代码去写的,导致一直卡用例,问gpt说什么会导致大集合被合并进入小集合,退化成链表。这些都不是本质原因。
然后洗澡的时候突然想明白了。本质原因还是无限递归。
下面开始正题。
一般并查集的p数组存在两种代表元初始化方法。
初始化为-1
这样表示每一个节点都是单独的。它所在的集合不存在代表元,即它就是该集合的代表元。这也是find操作的递归边界。
#include<iostream>
#include<vector>
using namespace std;
//并查集
int find(vector<int>&relations,int x){
//查找代表元
return (relations[x]==-1)? x:relations[x]=find(relations,relations[x]);
}
void Union(vector<int>&relations,int a,int b){
relations[find(relations,a)]=find(relations,b);
}
int main(){
int T;
cin>>T;
while(T--){
//n个亲戚,m个关系
int n,m;
cin>>n>>m;
vector<int>relations(n+1);
for(int i=0;i<=n;i++)
relations[i]=-1;
for(int i=0;i<m;i++){
int u,v;
cin>>u>>v;
Union(relations,u,v);
}
int query;
cin>>query;
//询问
for(int i=0;i<query;i++){
int a,b;
cin>>a>>b;
if(find(relations,a)==find(relations,b))
cout<<"Yes"<<endl;
else
cout<<"No"<<endl;
}
cout<<endl;
}
}
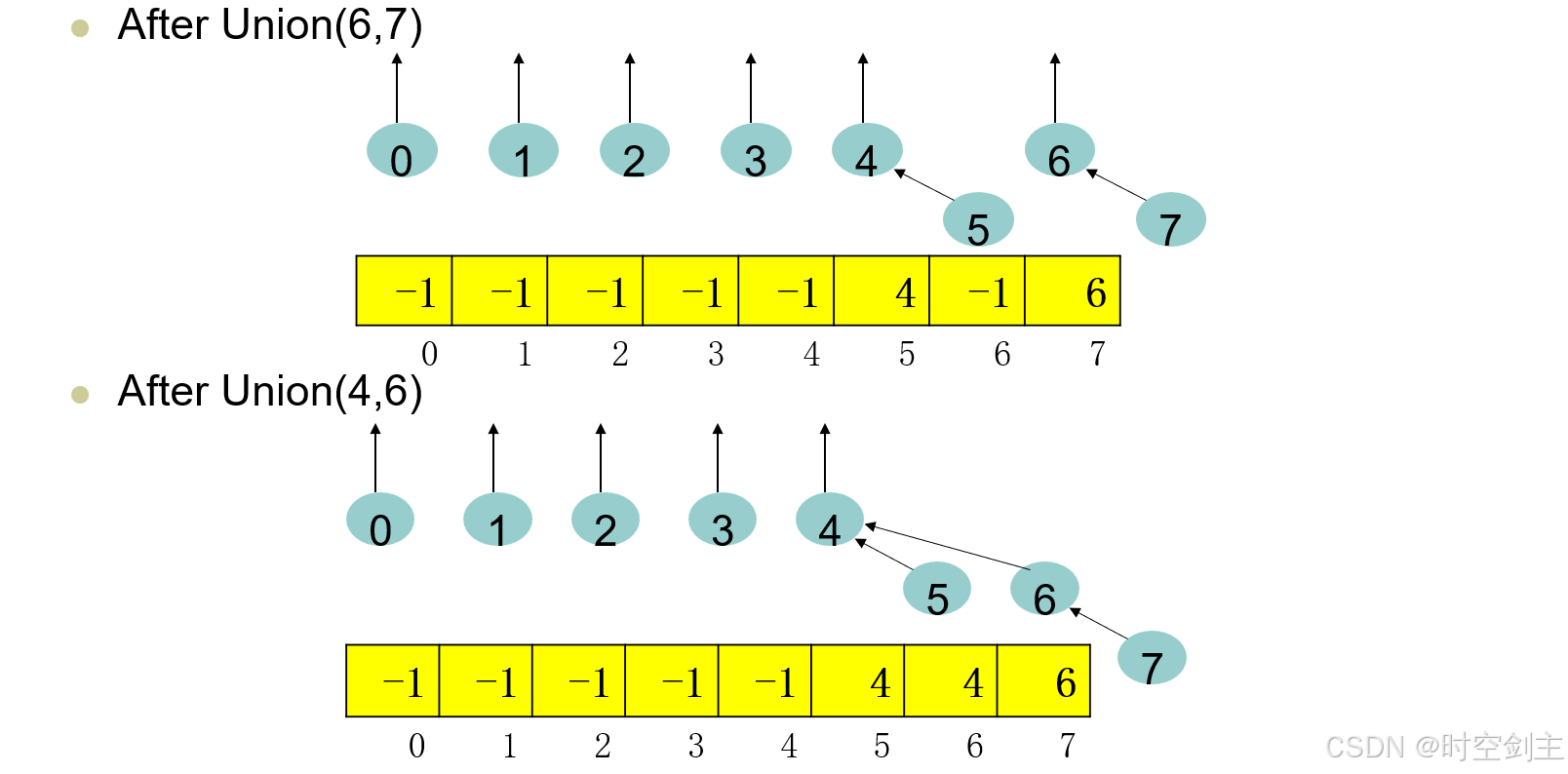
并查集的图解如下
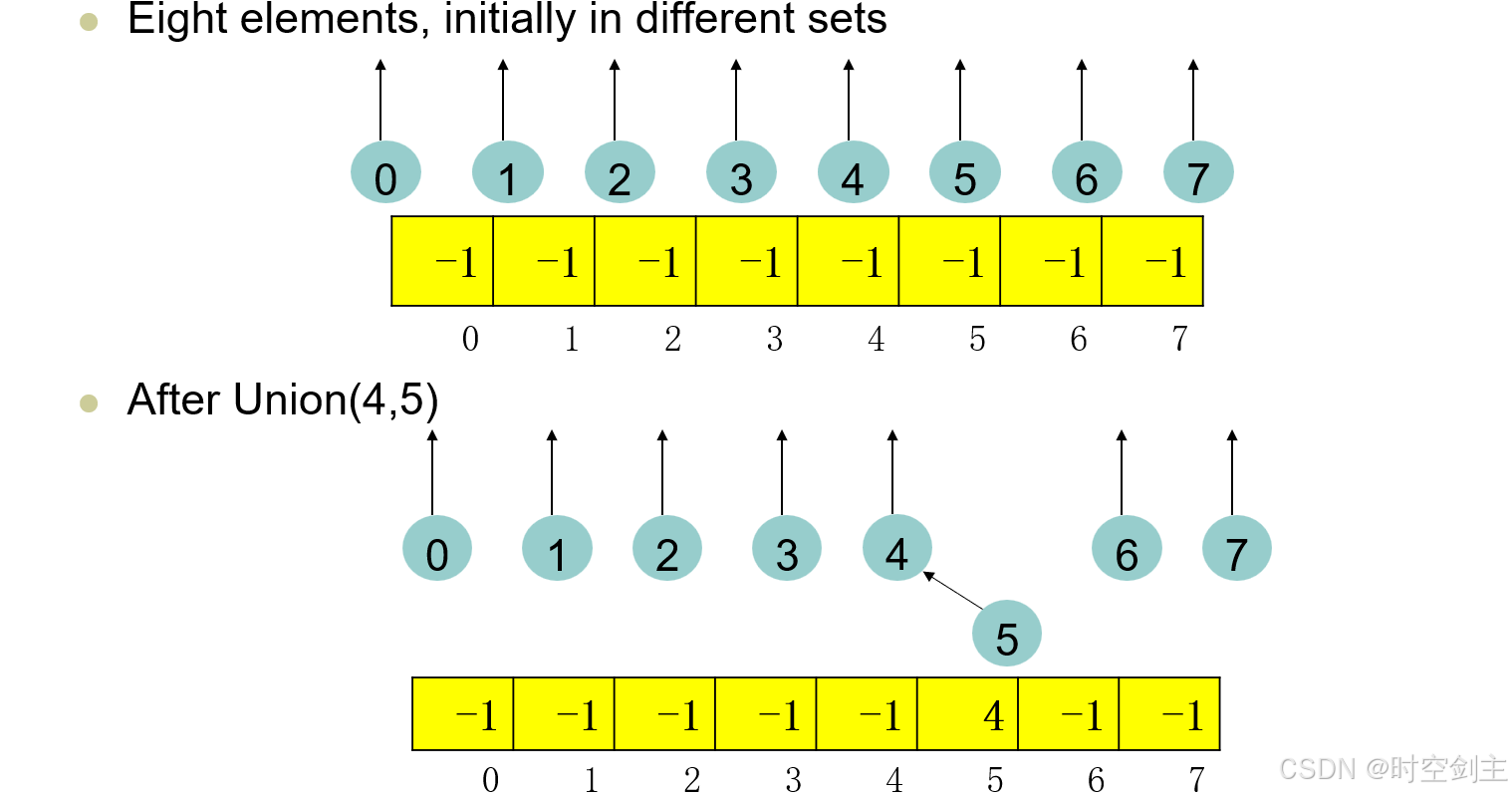
在进行查找find的时候,就会进行路径压缩,即在查找过程中对代表元进行更新,直接指向一开始的代表元,即递归边界
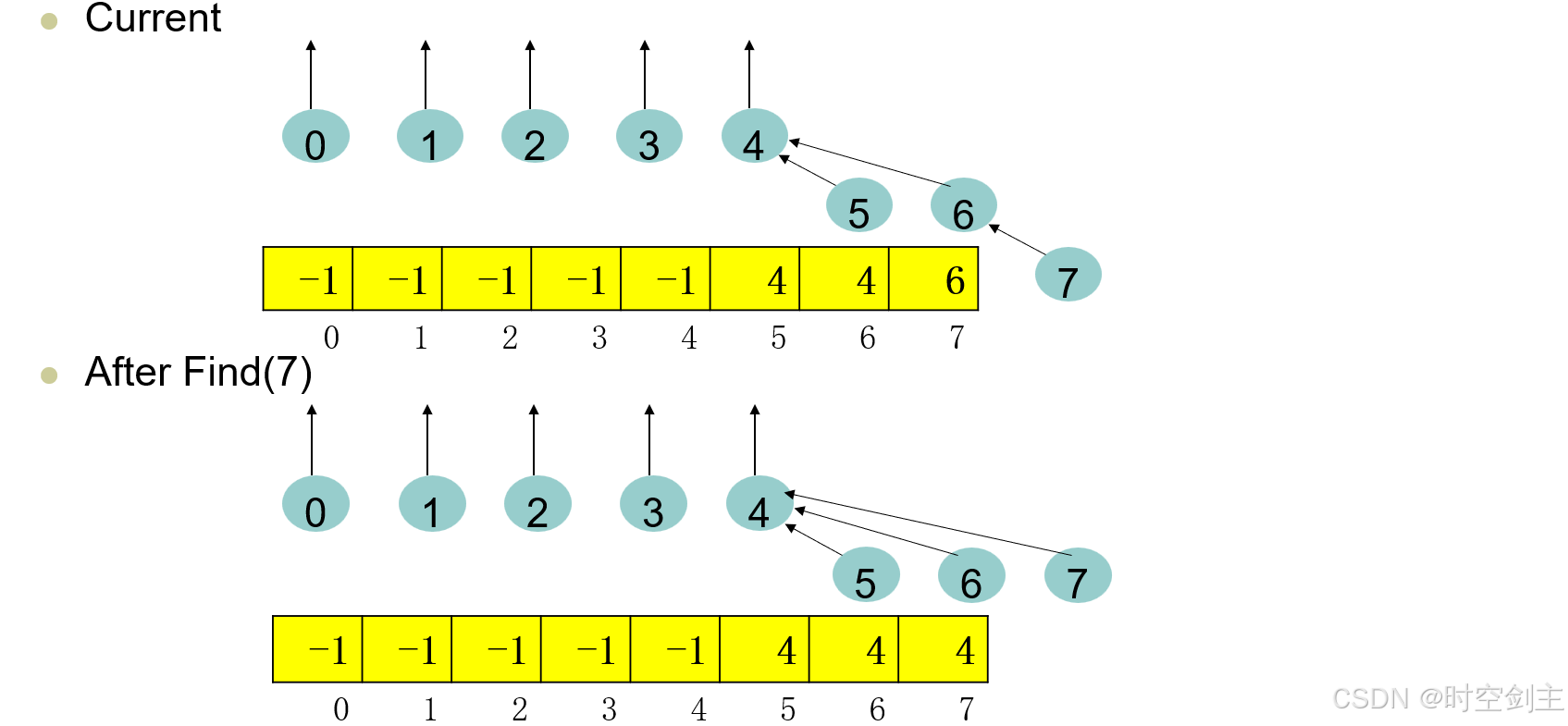
初始化为它本身
这个更好理解,就是每个点的代表元都是自己。
#include<iostream>
#include<vector>
using namespace std;
//并查集
int find(vector<int>&relations,int x){
//查找代表元
return (relations[x]==x)? x:relations[x]=find(relations,relations[x]);
}
void Union(vector<int>&relations,int a,int b){
relations[find(relations,a)]=find(relations,b);
}
//其余操作都是相同的,就省略了
vector<int>relations(n+1);
for(int i=0;i<=n;i++)
relations[i]=i;
求解过程
gpt给出的解答是要进行按秩优化,即防止树的高度线性增长过快。因此必须比较两个集合的高度大小,让小的集合被合并进入大的集合。
vector<int> rank(n + 1, 0); // 记录每棵树的秩(初始为 0)
// 合并两个集合,按秩优化
void unite(vector<int>& relations, vector<int>& rank, int x, int y) {
int rootX = find(relations, x);
int rootY = find(relations, y);
if (rootX != rootY) {
if (rank[rootX] > rank[rootY]) {
relations[rootY] = rootX; // 根Y挂到根X上
} else if (rank[rootX] < rank[rootY]) {
relations[rootX] = rootY; // 根X挂到根Y上
} else {
relations[rootY] = rootX; // 按秩合并
rank[rootX]++;
}
}
}
当然这个解答有点“弄拙成巧”的意味,的确过了测试用例。
少数据量的两种初始化:
初始化为-1:
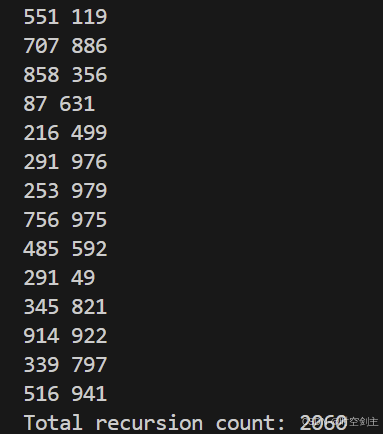
初始化为它本身: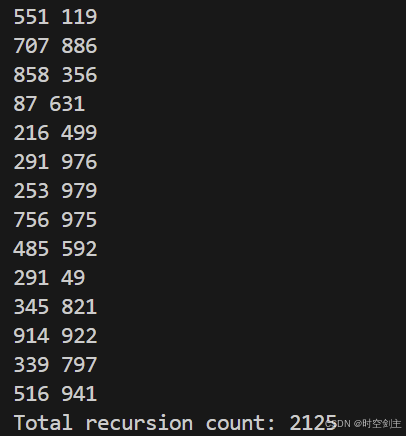
大数据量的两种初始化:
初始化为-1:
初始化为它本身:
其实差别并不大。
问题在哪里呢?
我在思考的时候发现了一个很有意思的地方,为什么gpt的答案要加一个判断代表元是否相等呢?
我将其去掉,发现程序同样崩溃了。
那么答案就很明显了。防止修改递归边界。
假设两个代表元相等,就是relations[find(k1)]=find(k2),find(k1)=find(k2)都是a。
听起来好像没问题,但它原本是relations[a]=-1,这样修改就会导致边界消失,无限递归了。
那我们只要在初始化为-1的情况进行修改Union操作即可
void Union(vector<int>&relations,int a,int b){
//不需要进行按秩优化
int k1=find(relations,a),k2=find(relations,b);
if(k1!=k2)
relations[k1]=k2;
}
大功告成,通过了。
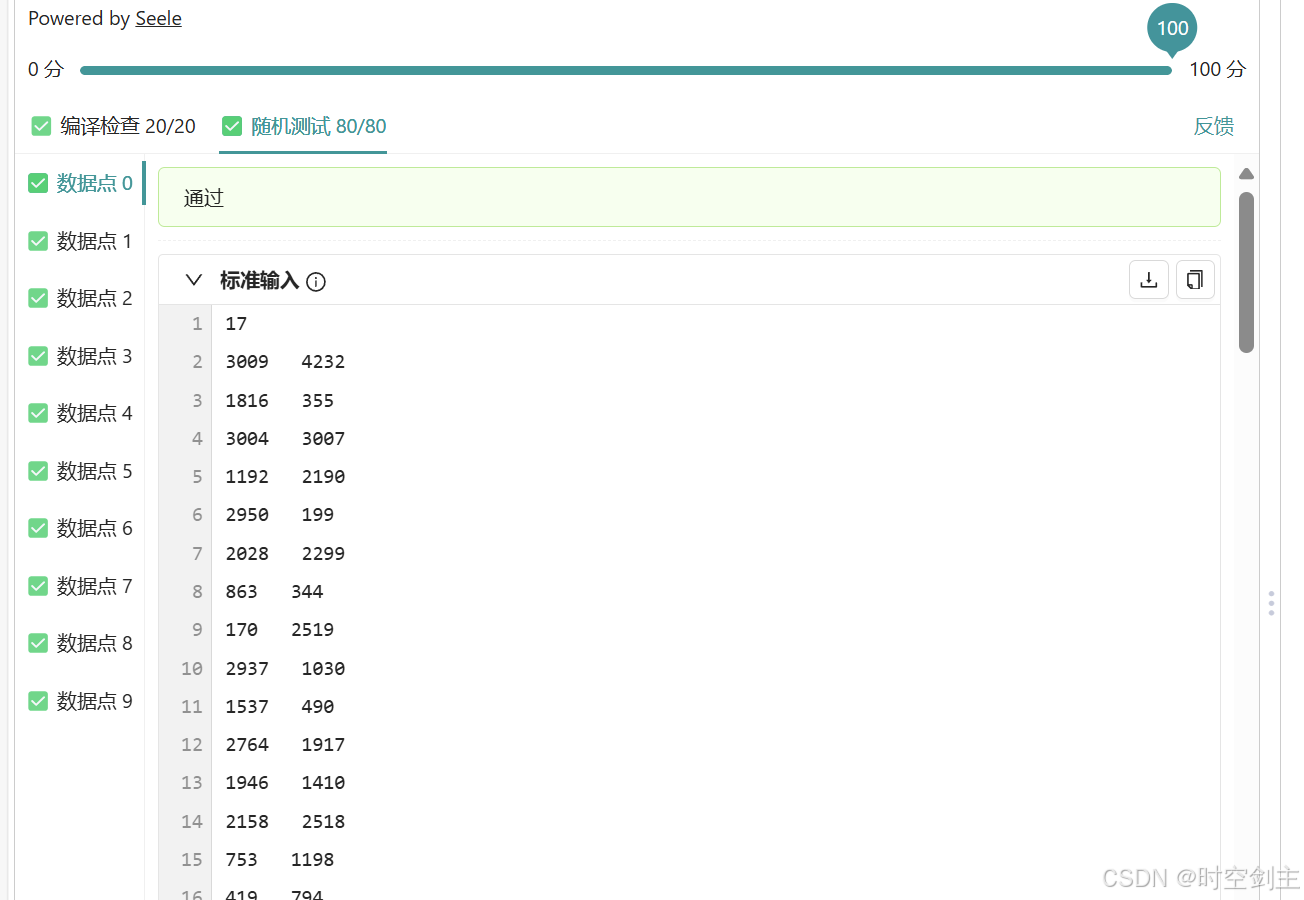




















 2263
2263

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








