目录
一.定义
Dynamic-Programing 由Bellman 提出
动态 编程
Programming - 在这里指用数学方法来根据子问题求解当前问题
Dynamic - 指缓存上一步结果,根据上一步结果计算当前结果(多阶段进行)
要点1:
- 从已知子问题的解,推导出当前问题的解
- 推导过程可以表达为一个数学公式
要点2:
- 用一维或二维数组来保存之前的计算结果(可以进一步优化)
合在一起:
- 将找出递归公式,将当前问题分解成子问题,分阶段进行求解
- 求解过程中缓存子问题的解,避免重复计算 n
- 入门练习
-
public static long fa(int n) { if (n==0) { return 0L; } if (n==1) { return 1L; } long a=0; long b=1; for (int i=2;i<n;i++) { long c=a+b;// 0+1 c=1 a=b;// a=1 b=c;// b=2 } return b; }
二.动态规划解决问题
1.零钱兑换问题
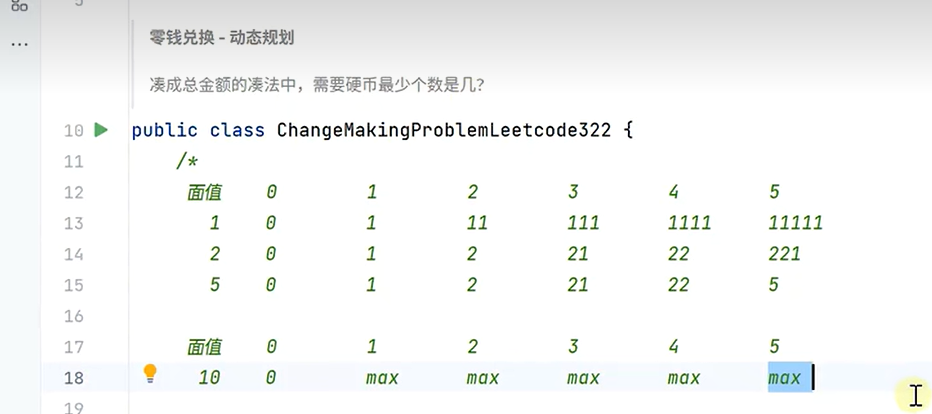
凑的总金额 -> 类比为背包容量
硬币面值 -> 类比为物体重量
硬币个数 -> 类比为物品价值,固定为1 求价值(个数)最小的

package com.shutu.DynamicPrograming;
public class ChangeMakingProblem {
public static void main(String[] args) {
changeMaking(new int[]{1,2,5},5);
}
public static void changeMaking(int[] coins, int amount) {
int[][]dp=new int[coins.length][amount+1];
dp[0][0]=0;
for (int i = 1; i <= amount; i++) {
if (coins[0]<=amount){
dp[0][i]=1+dp[0][i-coins[0]];
}else{
dp[0][i]=amount+1;// 硬币面额大于总金额 直接赋值为总金额+1
}
}
for (int i = 1; i < coins.length; i++) {
for (int j = 0; j <= amount; j++) {
if (coins[i]<=j){
// 当前面额小于等于总金额 可以选
dp[i][j]=Integer.min(dp[i-1][j],dp[i][j-coins[i]]+1);
}else{
dp[i][j]=dp[i-1][j];
}
}
}
for (int[] row : dp) {
for (int i : row) {
System.out.print(i+" ");
}
System.out.println();
}
// 如果硬币面额大于总金额 则返回-1
if (dp[coins.length-1][amount]<amount){
return dp[coins.length-1][amount];
}else{
return -1;
}
}
}空间优化-数组降维
public static int changeMaking(int[] coins, int amount) {
int[]dp=new int[amount+1];
dp[0]=0;
for (int i = 1; i <= amount; i++) {
if (coins[0]<=amount){
dp[i]=1+dp[i-coins[0]];
}else{
dp[i]=amount+1;
}
}
for (int i = 1; i < coins.length; i++) {
for (int j = 0; j <= amount; j++) {
if (coins[i]<=j){
// 当前面额小于等于总金额 可以选
dp[j]=Integer.min(dp[j],dp[j-coins[i]]+1);
}
}
}
if (dp[amount]<amount){
return dp[amount];
}else{
return -1;
}
}2.背包问题
2.1 0-1问题
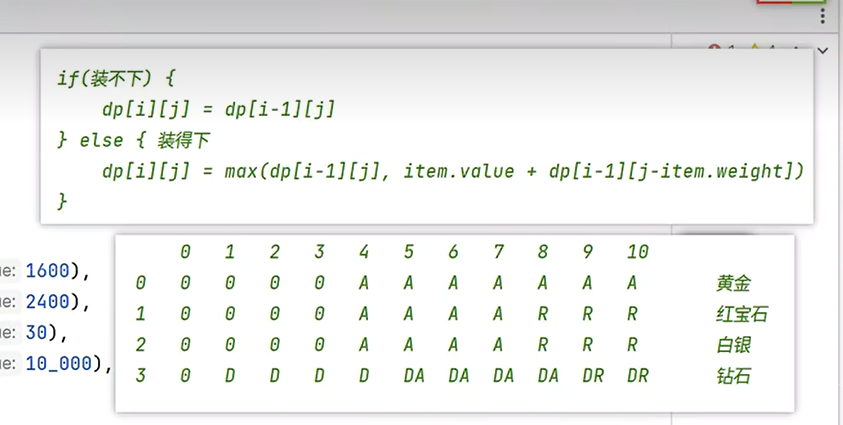
package com.shutu.DynamicPrograming;
import java.util.Arrays;
public class KnapsackProblem {
public static void main(String[] args) {
Item[] items = {new Item(1, "黄金", 4, 1600),
new Item(2, "宝石", 8, 2400),
new Item(3, "白银", 5, 30),
new Item(4, "钻石", 1, 10000)
};
System.out.println(select(items, 10));
}
private static int select(Item[] items, int total) {
int[][] dp = new int[items.length][total+1];
Item item = items[0];
for (int j = 0; j < total+1; j++) {
if (j<item.getValue()){
// 背包容量不足
dp[0][j] = 0;
}else{
// 容量足够
dp[0][j] = item.getWeight();
}
}
for (int i = 1; i < items.length ; i++) {
for (int j = 0; j < total+1; j++) {
if (j<items[i].getValue()){
// 背包容量不足
dp[i][j]=dp[i-1][j];
}else{
// 这里与完全背包问题区分开 0-1问题物品只可以拿一件 而完全背包物品无限制拿
// 这里用当前物品的价值+上一行这个容量能获取的最大价值 这样在拿的时候这个物品就只会拿一次
dp[i][j]=Integer.max(dp[i-1][j],items[i].getWeight()+dp[i-1][j-items[i].getValue()]);
}
}
for (int[] ints : dp) {
for (int ele : ints) {
System.out.print(ele+" ");
}
System.out.println();
}
}
return dp[items.length-1][total];
}
}空间优化降维为一维数组
private static int select(Item[] items, int total) {
int[] dp = new int[total + 1];
Item item0 = items[0];
for (int j = 0; j < total + 1; j++) {
if (j<item0.getValue()){
dp[j]=0;
}else{
dp[j]=item0.getWeight();
}
}
for (int i = 1; i < items.length; i++) {
Item item = items[i];
for (int j = total; j>0; j--) {
if (j<item.getValue()){
// 背包容量不够
dp[j]=0;
}else{
// 背包容量足够
int value=item.getWeight()+dp[j-item.getValue()];
dp[j]=Integer.max(dp[j],value);
}
}
}
return dp[total];
}
2.2 完全背包问题
0-1问题物品只可以拿一件 而完全背包问题可以无限制拿某件物品
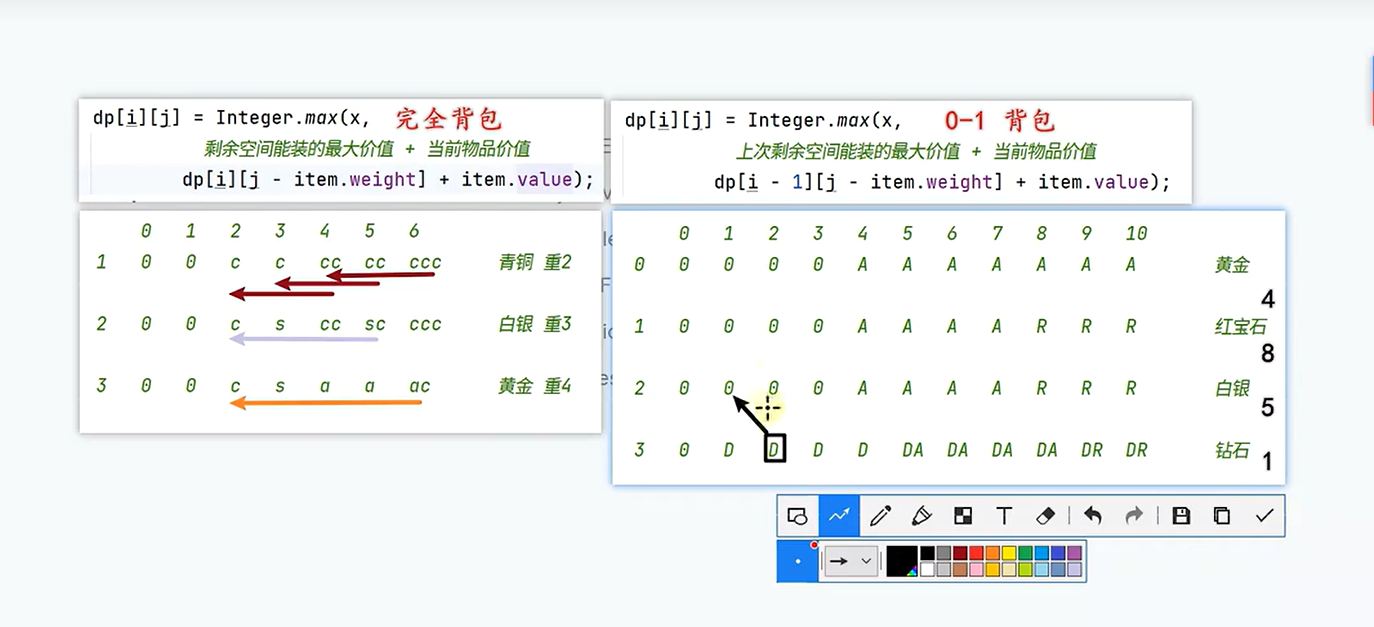
package com.shutu.DynamicPrograming;
public class KnapsackProblemComplete {
public static void main(String[] args) {
Item[] items = {new Item(1, "青铜", 3, 2),
new Item(2, "白银", 4, 3),
new Item(3, "黄金", 7, 4)
};
System.out.println(select(items, 6));
}
private static int select(Item[] items, int total) {
int[][] dp = new int[items.length][total + 1];
Item item0 = items[0];
for (int j = 0; j < total+1; j++) {
// 初始化背包
if (j<item0.getWeight()){
dp[0][j]=0;
}else{
// 这里不用取两者间最大值
dp[0][j]=dp[0][j-item0.getWeight()]+item0.getValue();
}
}
print(dp);
for (int i = 1; i < items.length; i++) {
Item item = items[i];
for (int j = 0; j < total+1; j++) {
if (j<item.getWeight()){
dp[i][j]=dp[i-1][j];
}else{
// 在当前行找剩余空间的最大值+当前物品的价值
dp[i][j]=Integer.max(dp[i-1][j],dp[i][j-item.getWeight()]+item.getValue());
}
}
print(dp);
}
return dp[items.length-1][total];
}
private static void print(int[][] dp) {
for (int[] ints : dp) {
for (int anInt : ints) {
System.out.print(anInt + " ");
}
System.out.println();
}
}
}
2.3 钢条切割问题
package com.shutu.DynamicPrograming;
public class KnapsackProblemComplete {
public static void main(String[] args) {
Item[] items = {new Item(1, "青铜", 3, 2),
new Item(2, "白银", 4, 3),
new Item(3, "黄金", 7, 4)
};
System.out.println(select(items, 6));
}
private static int select(Item[] items, int total) {
int[][] dp = new int[items.length][total + 1];
Item item0 = items[0];
for (int j = 0; j < total+1; j++) {
// 初始化背包
if (j<item0.getWeight()){
dp[0][j]=0;
}else{
// 这里不用取两者间最大值
dp[0][j]=dp[0][j-item0.getWeight()]+item0.getValue();
}
}
print(dp);
for (int i = 1; i < items.length; i++) {
Item item = items[i];
for (int j = 0; j < total+1; j++) {
if (j<item.getWeight()){
dp[i][j]=dp[i-1][j];
}else{
// 在当前行找剩余空间的最大值+当前物品的价值
dp[i][j]=Integer.max(dp[i-1][j],dp[i][j-item.getWeight()]+item.getValue());
}
}
print(dp);
}
return dp[items.length-1][total];
}
private static void print(int[][] dp) {
for (int[] ints : dp) {
for (int anInt : ints) {
System.out.print(anInt + " ");
}
System.out.println();
}
}
}
3.不同路径问题

自己加上左边的数等于自己的新数

class Solution {
public int uniquePaths(int m, int n) {
// m*n 竖着走m-1 横着走n-1
// 2 6
// int[][] dp=new int[m][n];
// // 初始化行值
// for(int i=0;i<n;i++){
// dp[0][i]=1;
// }
// // 初始化列值
// for(int j=0;j<m;j++){
// dp[j][0]=1;
// }
// for(int i=1;i<m;i++){
// for(int j=1;j<n;j++){
// dp[i][j]=dp[i-1][j]+dp[i][j-1];
// }
// }
// return dp[m-1][n-1];
// 空间优化降维 类似杨辉三角形
int[]dp=new int[n];
for(int i=0;i<n;i++){
dp[i]=1;
}
for(int j=1;j<m;j++){
for(int i=1;i<n;i++){
dp[i]=dp[i-1]+dp[i];
}
}
return dp[n-1];
}
}4.最长公共子串
求解方法
最长公共子串问题通常通过动态规划(Dynamic Programming, DP)来解决。以下是使用动态规划求解最长公共子串的基本步骤:
1.定义状态:
- 定义一个二维数组
dp,其中dp[i][j]表示字符串s1的前i个字符和字符串s2的前j个字符之间的最长公共子串的长度。
2.初始化:
- 将
dp数组的所有元素初始化为0,因为空字符串之间的最长公共子串长度为0。
3.状态转移:
- 如果
s1[i-1] == s2[j-1](即当前字符相等),则dp[i][j] = dp[i-1][j-1] + 1。这表示找到了一个更长的公共子串。 - 如果
s1[i-1] != s2[j-1](即当前字符不相等),则dp[i][j] = 0。因为当前字符不相等,所以它们不能构成公共子串的一部分。
4.记录结果:
- 在填充
dp数组的过程中,同时记录最长公共子串的长度以及它在两个字符串中的结束位置。 - 知道结束位置和长度,即可得出开始的位置
5.构造最长公共子串:
- 根据记录的结束位置和最长长度,从后往前构造出最长公共子串。
public class LCSubstring {
public static void main(String[] args) {
System.out.println(lcs("thema", "itheima"));
}
public static int lcs(String a,String b){
char[] charArray = a.toCharArray();
char[] charArray2 = b.toCharArray();
int[][] dp = new int[charArray.length][charArray2.length];
/*
0 1 0 0 0 0 0
0 0 2 0 0 0 0
0 0 0 3 0 0 0
0 0 0 0 0 1 0
0 0 0 0 0 0 2
*/
int max = 0;
for (int i = 0; i <charArray2.length ; i++) {
if (charArray[0]==charArray2[i]){
dp[0][i]=1;
}
}
for (int i = 1; i < charArray.length ; i++) {
for (int j = 1; j < charArray2.length; j++) {
if (charArray[i]==charArray2[j]){
dp[i][j]=dp[i-1][j-1]+1;
max=Integer.max(max,dp[i][j]);
i++;
}
}
}
for (int[] ints : dp) {
for (int anInt : ints) {
System.out.print(anInt+" ");
}
System.out.println();
}
System.out.println();
return max;
}
}5.最长公共子序列
思路:
- 定义一个二维数组dp,其中dpi,j表示序列A的前i个元素和序列B的前j个元素的长度。
- 初始化dp数组,将dp0,j和dpi,0都设置为0,表示空序列的长度为0。
- 遍历序列A和序列B的所有元素,对于每个元素,如果字符相等,dp[i][j]=dp[i-1][j-1]+1;否则,dp[i][j]=max(dp[i-1][j],dp[i][j-1])。
- 最终结果为dp[m][n],其中m和n分别为序列A和序列B的长度。
public class LCR {
public int longestCommonSubsequence(String text1, String text2) {
int[][]dp=new int[text1.length()+1][text2.length()+1];
char[] charArray = text1.toCharArray();
char[] charArray2 = text2.toCharArray();
/**
0 a b c d e
0
a 1 1 1 1 1
c 1 1 2 2 2
e 1 1 2 2 3
*/
for(int i=1;i<=text1.length();i++){ // 在下面拿到字符串时是i-1 所以要<=
for(int j=1;j<=text2.length();j++) {
if(charArray[i-1]==charArray2[j-1]){
// 两个字符相等 在对角线上找上一个值
dp[i][j]=dp[i-1][j-1]+1;
}else{
// 在上一行和上一列中找较大值
dp[i][j]=Integer.max(dp[i-1][j],dp[i][j-1]);
}
}
}
return dp[text1.length()][text2.length()];
}
}应用场景
最长公共子序列问题十分实用,它可以描述两段文字之间的“相似度”,即它们的雷同程度,从而能够用来辨别抄袭或计算文本差异等。例如,对一段文字进行修改之后,计算改动前后文字的最长公共子序列,将除此子序列外的部分提取出来,这种方法判断修改的部分往往十分准确。
6.最长递增子序列

思路:
- 从前往后遍历,相对顺序一定,则就是子序列
- 使用一维数组记录到每个数时的最长子序列的长度
- 在当前该位已求的子序列长度和上一位小于当前值的数+1中选出较大值

public int lengthOfLIS(int[] nums) {
/**
* 1 3 6 4 9
* 1 13 16 14 19
* 136 134 139
* 169
* 1369
* 149
* 1349
*/
int[] dp = new int[nums.length];
Arrays.fill(dp,1);
for (int i = 0; i < nums.length; i++) {
for (int j = 0; j < i; j++) {
if (nums[i]>nums[j]){
// 当前数大于之前的数 递增 正序遍历已是子序列
dp[i]=Integer.max(dp[i],dp[j]+1);
}
}
}
return Arrays.stream(dp).max().getAsInt();
}






















 3054
3054

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








