【自然语言处理】Transformer 模型中的专家混合（Mixture of Experts,MoE）架构

原创 已于 2025-09-13 09:35:07 修改 · 3k 阅读 · 20 ·
CC 4.0 BY-SA版权
原创文章，禁止转载，否则保留追究法律责任的权利。
文章标签：

#transformer #深度学习 #自然语言处理

于 2025-09-13 09:33:54 首次发布
部署运行你感兴趣的模型镜像

【精选优质专栏推荐】


每个专栏均配有案例与图文讲解，循序渐进，适合新手与进阶学习者，欢迎订阅。

文章目录

在这里插入图片描述

Transformer 模型在许多自然语言处理任务中表现出极高的有效性。虽然通过增加模型维度和层数可以提升其能力，但这也会显著增加计算复杂度。专家混合（Mixture of Experts, MoE）架构提供了一种优雅的解决方案：通过引入稀疏性，使模型能够高效扩展，而无需按比例增加计算成本。

在本文中，你将了解 Transformer 模型中的专家混合架构，具体包括：

  • 为什么 MoE 架构对于高效扩展 Transformer 模型是必要的

  • MoE 的工作原理及其关键组成部分

  • 如何在 Transformer 模型中实现 MoE

为什么 Transformer 需要专家混合架构

专家混合（Mixture of Experts, MoE）概念最早由 Jacobs 等人在 1991 年提出。它使用多个“专家”模型处理输入，并通过“门控”机制选择使用哪一个专家。

MoE 在 2021 年的 Switch Transformer 和 2024 年的 Mixtral 模型中得到了复兴。在 Transformer 模型中，MoE 对每个输入仅激活部分参数，这使得可以定义大规模模型，同时每次计算只使用其中的一部分。

以 Mixtral 模型架构为例：

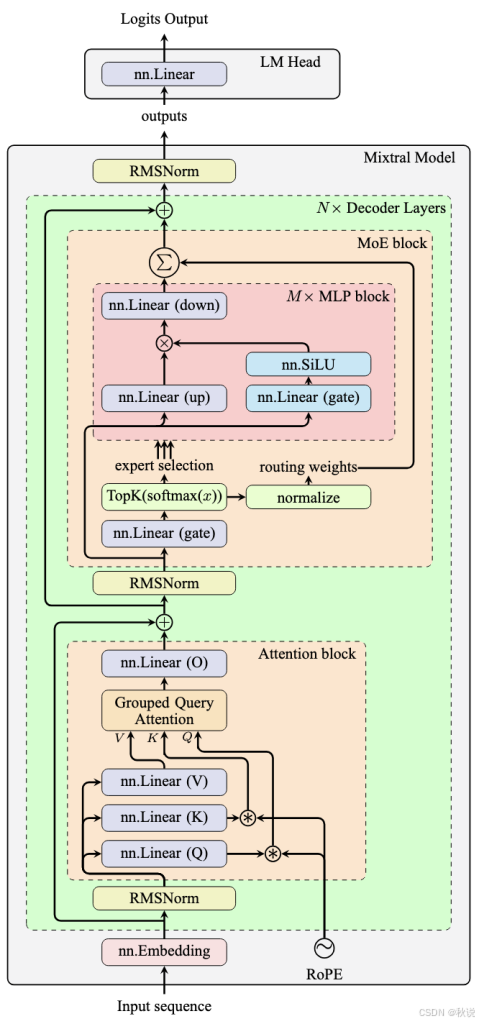
在这里插入图片描述

如前文所述，MLP 块为 Transformer 层引入了非线性，而注意力块仅通过线性组合对输入序列的信息进行重组。Transformer 模型的“智能”主要体现在 MLP 块中。

这也解释了为什么 MLP 块通常包含 Transformer 模型中最多的参数和计算负载。训练 MLP 块以在各种任务上表现良好具有挑战性，因为不同任务可能需要相互矛盾的行为。

一种解决方案是为每个任务创建专门的模型，并使用路由器选择合适的模型。另一种方法是将多个模型和路由器合并为一个单一模型，并一并训练。MoE 的核心正是这一思想。

MoE 通过引入稀疏性实现这一点：多个专家网络中每次只激活稀疏子集。MoE 架构仅修改 MLP 块，而所有专家共享同一个注意力块。每个 Transformer 层拥有独立的一组专家，使各层之间可以自由组合。这允许创建大量专家而不显著增加参数总量，从而在扩展模型的同时保持较低计算成本。

核心观点是：不同的输入适合不同的专门化计算。通过拥有多个专家网络并配合路由机制选择使用的专家，模型能够以更少的计算资源实现更优的性能。

专家混合（MoE）的工作原理

MoE 架构由三个关键组件组成：

  1. 专家网络（Expert Networks）：
    多个独立的神经网络（专家）处理输入，类似于其他 Transformer 模型中的 MLP 块。

  2. 路由器（Router）：
    决定哪些专家处理每个输入的机制。通常由一个线性层加 softmax 组成，生成针对 N N N 个专家的概率分布。路由器输出通过“门控机制”选择前 k k k 个专家。

  3. 输出组合（Output combination）：
    前 k k k 个专家处理输入，并根据路由器归一化概率的加权和组合输出。

基本 MoE 操作如下：对于来自注意力块输出序列的每个向量 x x x，路由器将其与矩阵相乘生成 logits（图中门控层）。经过 softmax 转换后，这些 logits 通过前 k k k 操作筛选，得到 k k k 个索引和 k k k 个概率。索引用于激活专家（图中 MLP 块），处理原始注意力块输出。专家输出按路由器归一化概率加权求和，得到最终结果。

概念上，MoE 块计算公式为：

MoE ( x ) = ∑ i ∈ TopK ( p ) p i ⋅ Expert i ( x ) \text{MoE}(x) = \sum_{i \in \text{TopK}(p)} p_i \cdot \text{Expert}_i(x) MoE(x)=i∈TopK(p)∑​pi​⋅Experti​(x)

其中 k k k 是模型超参数，即使 k = 2 k=2 k=2 通常也能获得良好性能。

在 Transformer 模型中实现 MoE

下面是一个使用 PyTorch 实现的 Transformer 层示例，其中 MoE 替代了传统的 MLP 块：

import torch
import torch.nn as nn
import torch.nn.functional as F

class Expert(nn.Module):
    def __init__(self, dim, intermediate_dim):
        super().__init__()
        self.gate_proj = nn.Linear(dim, intermediate_dim)
        self.up_proj = nn.Linear(dim, intermediate_dim)
        self.down_proj = nn.Linear(intermediate_dim, dim)
        self.act = nn.SiLU()

    def forward(self, x):
        gate = self.gate_proj(x)
        up = self.up_proj(x)
        swish = self.act(gate)
        output = self.down_proj(swish * up)
        return output

class MoELayer(nn.Module):
    def __init__(self, dim, intermediate_dim, num_experts, top_k=2):
        super().__init__()
        self.num_experts = num_experts
        self.top_k = top_k
        self.dim = dim
        self.experts = nn.ModuleList([
            Expert(dim, intermediate_dim) for _ in range(num_experts)
        ])
        self.router = nn.Linear(dim, num_experts)

    def forward(self, hidden_states):
        batch_size, seq_len, hidden_dim = hidden_states.shape
        hidden_states_reshaped = hidden_states.view(-1, hidden_dim)
        router_logits = self.router(hidden_states_reshaped)
        routing_probs = F.softmax(router_logits, dim=-1)

        top_k_probs, top_k_indices = torch.topk(routing_probs, self.top_k, dim=-1)
        top_k_probs = top_k_probs / top_k_probs.sum(dim=-1, keepdim=True)

        output = []
        for i in range(self.top_k):
            expert_idx = top_k_indices[:, i]
            expert_probs = top_k_probs[:, i]
            expert_output = torch.stack([
                self.experts[exp_idx](hidden_states_reshaped[j])
                for j, exp_idx in enumerate(expert_idx)
            ], dim=0)
            output.append(expert_probs.unsqueeze(-1) * expert_output)

        output = sum(output).view(batch_size, seq_len, hidden_dim)
        return output

class MoETransformerLayer(nn.Module):
    def __init__(self, dim, intermediate_dim, num_experts, top_k=2, num_heads=8):
        super().__init__()
        self.attention = nn.MultiheadAttention(dim, num_heads, batch_first=True)
        self.moe = MoELayer(dim, intermediate_dim, num_experts, top_k)
        self.norm1 = nn.RMSNorm(dim)
        self.norm2 = nn.RMSNorm(dim)

    def forward(self, x):
        input_x = x
        x = self.norm1(x)
        attn_output, _ = self.attention(x, x, x)
        input_x = input_x + attn_output

        x = self.norm2(input_x)
        moe_output = self.moe(x)
        return input_x + moe_output

完整的 MoE Transformer 模型由多个此类 Transformer 层组成，每层包含注意力子层和 MoE 子层，其中 MoE 子层类似于传统 Transformer 中的 MLP 子层。

在 MoELayer 类中，forward() 方法的输入形状为 (batch_size, seq_len, hidden_dim)。由于每个序列向量独立处理，输入首先被重塑为 (batch_size * seq_len, hidden_dim)。路由器和 softmax 生成 routing_probs，形状为 (batch_size * seq_len, num_experts)，表示每个专家对输出的贡献。

top-k 操作选择专家及其对应概率。在 for 循环中，每个向量由对应专家处理，并将输出堆叠在一起。循环生成一个加权张量列表 output，最终求和得到输出，并重塑回原始形状 (batch_size, seq_len, hidden_dim)。

Expert 类与前文中的 MLP 块相同，但 MoE 子层使用多个实例，而不是单个 Transformer 层中的 MLP。

我们可以使用以下代码测试 Transformer 层：

batch_size = 4
seq_len = 10
dim = 16
intermediate_dim = 72
num_experts = 8

x = torch.randn(batch_size, seq_len, dim)
model = MoETransformerLayer(dim, intermediate_dim, num_experts)
y = model(x)

共享专家（Shared Experts）

上述实现是最简单的 MoE 架构。最近，DeepSeek 模型提出并推广了一种新思路：在 MoE 架构中加入少量“共享专家”，这些共享专家会对任何输入始终被使用。数学上，MoE 的计算公式变为：

MoE ( x ) = Expert ∗ ( x ) + ∑ i ∈ TopK ( p ) p i ⋅ Expert i ( x ) \text{MoE}(x) = \text{Expert}^*(x) + \sum_{i \in \text{TopK}(p)} p_i \cdot \text{Expert}_i(x) MoE(x)=Expert∗(x)+i∈TopK(p)∑​pi​⋅Experti​(x)

其中额外的专家就是共享专家。显然，你可以使用多个共享专家。在所有情况下，共享专家不依赖路由器，而是无条件处理输入。

要实现共享专家，可以复用前面的代码，并在 MoETransformerLayer 类中添加额外的专家网络：

class MoETransformerLayer(nn.Module):
    def __init__(self, dim, intermediate_dim, num_experts, top_k=2, num_heads=8, num_shared_experts=1):
        super().__init__()
        self.attention = nn.MultiheadAttention(dim, num_heads, batch_first=True)
        self.moe = MoELayer(dim, intermediate_dim, num_experts, top_k)
        # 共享专家
        self.shared_experts = nn.ModuleList([
            Expert(dim, intermediate_dim) for _ in range(num_shared_experts)
        ])
        self.norm1 = nn.RMSNorm(dim)
        self.norm2 = nn.RMSNorm(dim)

    def forward(self, x):
        # 注意力子层
        input_x = x
        x = self.norm1(x)
        attn_output, _ = self.attention(x, x, x)
        input_x = input_x + attn_output

        # MoE 子层
        x = self.norm2(input_x)
        moe_output = self.moe(x)
        for expert in self.shared_experts:
            moe_output += expert(x)
        return input_x + moe_output

总结

本文详细介绍了 Transformer 模型中的专家混合（MoE）架构及其实现方法。通过引入多个专家网络和路由机制，MoE 能在保证计算效率的前提下扩展模型规模，提高对不同输入的处理能力。

掌握 MoE 架构后，可在实际项目中针对不同任务灵活设计专家网络，提升模型性能，同时控制计算成本，为大规模 Transformer 模型的高效部署提供基础。

您可能感兴趣的与本文相关的镜像

Qwen3-14B

Qwen3-14B

文本生成
Qwen3

Qwen3 是 Qwen 系列中的最新一代大型语言模型，提供了一整套密集型和专家混合（MoE）模型。基于广泛的训练，Qwen3 在推理、指令执行、代理能力和多语言支持方面取得了突破性进展

8类CNN-Transformer混合架构魔改方案盘点，附23个配套模型＆代码
学姐带你玩AI的博客
01-17 1万+
为进一步提高模型的性能，我们将。目前，它已经成为我们研究视觉任务、发文章离不开的模型。针对CNN+transformer组合方向的研究也成为了当下计算机视觉领域研究中的大热主题。CNN-Transformer架构凭借众所周知的优势，在视觉任务上取得了令人瞩目的效果，它不仅可以提高模型在多种计算机视觉任务中的性能，还能实现较好的延迟和精度之间的权衡。为挖掘CNN-Transformer混合架构更多的潜力，有关于它的各种变体的研究也逐步增多。为了方便同学们了解，我这次就和大家分享该架构。
大模型基石：Transformer架构深度拆解，一文读懂核心原理
大模型研究中心
09-25 1300
大模型基石：Transformer架构深度拆解，一文读懂核心原理
技术前沿 |【大型深度学习模型中的多面手：混合专家（Mixture of Experts，MoE）机制详解】
尺小闹的博客
05-10 3890
本文将带您走进MoE的世界，了解其基本概念、原理、应用场景以及与其他注意力机制的比较，并对未来的发展进行展望。不同的专家模型可以处理不同类型的输入或任务部分，从而实现对复杂任务的全面覆盖。这些专家模型各自擅长处理不同的输入或任务部分，而MoE机制则负责根据输入的特点动态地选择最合适的专家模型进行处理。MoE机制可以根据输入的特点动态地选择最合适的专家模型进行处理，因此具有很高的灵活性。相比之下，传统的注意力机制通常只能对输入进行固定的处理，无法根据输入的特点进行动态调整。
边缘计算(一)：EdgeNeXt，面向移动开发的CNN-Transformer混合架构
wqthaha的专栏
06-23 3475
CNN和Transformer单独玩出的花样层出不穷。你中有我我中有你的思想，交替出现，例如Large Kernel CNN试图去模仿Transformer的远程建模能力，Local Transformers试图去模仿CNN分层建模的能力。
【大模型理论篇】Mixture of Experts(混合专家模型, MOE)
热门推荐
源泉的小广场
08-25 1万+
大模型、transformer、混合专家模型、MoE、mixture of experts、稀疏性、模型算力、LLM、SMoE、gemini、mixtral、万亿参数大模型、门控机制、专家混合
Transformer与混合专家（MoE）：大型语言模型的架构对比
kaka0722ww的博客
03-20 2315
Transformer与混合专家（MoE）代表了大型语言模型发展的两个重要阶段。Transformer以其简洁高效的架构奠定了NLP的基础，而MoE通过引入专家机制，进一步突破了性能和效率的瓶颈。尽管MoE在训练中面临专家均衡性等挑战，但通过路由器优化和容量限制等解决方案，它已成为构建更强大语言模型的重要工具。未来，随着技术的不断进步，MoE有望在更多场景中大放异彩，推动NLP领域迈向新的高度。
Transformer与混合专家（MoE）：大型语言模型的架构对比_moe架构和transformer架构
HUANGXIN9898的博客
04-15 1297
Transformer与混合专家（MoE）代表了大型语言模型发展的两个重要阶段。Transformer以其简洁高效的架构奠定了NLP的基础，而MoE通过引入专家机制，进一步突破了性能和效率的瓶颈。尽管MoE在训练中面临专家均衡性等挑战，但通过路由器优化和容量限制等解决方案，它已成为构建更强大语言模型的重要工具。未来，随着技术的不断进步，MoE有望在更多场景中大放异彩，推动NLP领域迈向新的高度。
一文图解混合专家模型(Mixture of Experts, MoE)
Q2024107的博客
08-07 996
摘要：混合专家模型(MoE)是一种通过选择性激活专家网络来提升效率的机器学习架构。其核心由专家网络和门控网络组成，仅激活相关专家处理特定输入，在保持高模型容量的同时降低计算成本。典型应用包括Mixtral-8x7B等大模型，相比稠密模型具有更快的预训练和推理速度。但MoE也面临训练泛化性差、显存需求大等挑战，如Mixtral-8x7B需要加载47B参数到内存。该技术通过条件计算实现稀疏性，但需解决专家负载均衡等问题。(149字)
MoE（Mixture of Experts，混合专家模型）
m0_66855407的博客
10-22 866
要理解所谓的专家，容易把在图片中的每一层的每一个专家或者小的网络模型理解成具体学习的是不同的知识，例如专家一学习Psychology的知识，专家三学习Biology的知识，每个专家都有自己学习的能力和内容，但是，在真正的执行当中，或者真正的数学计算和模型结构学的不是所谓的这些专家知识，而是学习syntactic information所谓的。，在最原始的文章里面说到是一个门控网络通过一个开关去决定选择不同的专家，随着大家对整个计算的认识，就把它变成Router，主要是指路由去决定输入。
### 深度学习从Transformer到Mixture of Experts（MoE）：大模型架构演进及其应用
04-09
内容概要：本文详细介绍了大模型架构从Transformer到Mixture of Experts (MoE)的演进过程。首先阐述了Transformer架构的基础原理，包括自注意力机制、多头注意力机制和位置编码等，以及其在自然语言处理和计算机视觉...
精选资源
深度学习领域中高效开源MoE架构语言模型DeepSeek-V2的技术解析与应用
03-30
内容概要：本文介绍了DeepSeek-V2，一款基于Mixture-of-Experts (MoE) 架构的高性能开源大型语言模型。它拥有236亿参数，每次推理激活21亿参数，显著降低了训练成本（节省42.5%）并提高了推理效率（KV缓存减少93.3%...
大模型架构演进：从Transformer到Mixture of Experts（MoE）
qq_40552871的博客
04-04 1125
Transformer架构是大模型发展的重要基石，其核心原理基于自注意力机制（Self-Attention Mechanism）。在传统的循环神经网络（RNN）架构中，信息的传递是按顺序进行的，这使得模型在处理长序列数据时效率低下且难以捕捉长距离依赖关系。而Transformer架构通过自注意力机制，能够让模型在处理序列数据时，同时考虑序列中所有位置的信息，从而更高效地捕捉长距离依赖关系。
MoE（Mixture of Experts，混合专家模型
汽车软件开发
05-03 1210
MoE模型支持用较少的算力预训练大模型，这意味着可以在有限的算力预算下训练出比稠密模型大得多的稀疏模型，或者在更大的数据集上进行训练。例如，尽管只有较少的参数，但MoE模型的性能可以媲美传统的更大参数模型，在推理速度上也显著超越了其他同类模型。- 特定领域的应用：在计算机视觉（CV）领域，可以采用single-gated MoE模型，该模型在推理时计算成本合理，适用于训练大规模模型。- 解决多模态大模型冲突的方法：通过利用稀疏专家模型（MoE），不同的专家处理不同的任务，并设计一种数据划分的方法。
Mixture of Experts（MoE）的架构
百态老人的博客
01-30 1426
Mixture of Experts（MoE）是一种先进的深度学习架构，旨在通过动态选择部分专家子网络来处理输入数据，从而提高模型的计算效率和性能。其核心思想是将复杂任务分解为多个子任务，由不同的专家网络分别处理，再通过门控机制整合各专家的输出，以实现更高的模型精度和资源利用率。
Day44 简单 CNN 实战
W020419的博客
12-26 339
将卷积输出展平成向量，接 1~2 层全连接 + Dropout，输出 10 维 logits。：BatchNorm 稳定分布、Dropout 降低 co-adaptation。这些中间输出就是“特征图”，可借助 Grad-CAM 等方法做可视化解释。第 3 个卷积块：池化后得到 128×4×4，展平即 2048 维向量。第 1 个卷积块：保持尺寸，池化后得到 32×16×16；第 2 个卷积块：池化后得到 64×8×8；提取多尺度特征并逐步减小空间维度。
Day46
m0_70488789的博客
12-26 278
作业：手动构造类似的数据集（如cosx数据），观察不同的机器学习模型的差异。4. 经典机器学习在序列任务上的劣势；# DAY 46 序列预测任务介绍。b. 多步预测的2种方式。2. 序列数据的处理：滑动窗口。3. 多输入多输出任务的思路。
【深度学习新浪潮】本地文档总结引擎部署全攻略（二）：增量更新、自定义模板与实战汇报生成
最新发布
全网同名。更多请搜索wx公众号：浮游会。
12-31 128
基础系统的总结格式由固定，无法满足不同汇报场景（如周汇报、月汇报、项目总结）的需求。通过自定义Prompt模板，我们可以定义灵活的输出格式，支持模板变量（如文档名称、时间范围、汇报人）。在from llama_index . core . prompts import PromptTemplate from llama_index . core . query_engine import CustomQueryEngine # 定义常用汇报模板 REPORT_TEMPLATES = {
深度学习—卷积神经网络（2）
renjt01的博客
12-30 88
深度学习—卷积神经网络（2） 2.DNN与CNN的区别 3.卷积的数学定义 4.CNN的结构组成 卷积层 #人工智能#具身智能#VLA#大模型#AI#LLM#Transformer 架构#AI技术前沿#Agent大模型#工信部证书#人工智能证书#职业证书
毕业项目推荐：91-基于yolov8/yolov5/yolo11的井盖破损检测识别（Python+卷积神经网络）
weixin_71667732的博客
12-29 767
项目中所用到的算法模型和数据集等信息如下：算法模型：yolov8yolov8 + SE注意力机制或yolov5yolov5 + SE注意力机制或yolo11yolo11 + SE注意力机制数据集：网上下载的数据集，格式都已转好，可直接使用。以上是本套代码算法的简单说明，添加注意力机制是本套系统的创新点。全新SOTA模型YOLOv8 提供了全新的最先进（SOTA）的模型，包括P5 640和P6 1280分辨率的目标检测网络，同时还推出了基于YOLACT的实例分割模型。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

秋说

感谢打赏

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值