24下软考中级软件设计师，就剩几天了！

这几页纸，快背！

一 计算机组成与体系结构

1、寻址方式：立即寻址最快（操作数本身），寄存器寻址次之（操作数地址的地址），直接寻址最慢（操作数的地址）。

2、数据传输方式

（1）程序控制（查询）方式：分为无条件传送和程序查询方式两种。方法简单，硬件开销小，但I/O能力不高，严重影响CPU的利用率（不可与CPU并行）。

（2）程序中断方式：与程序控制方式相比，中断方式因为CPU无需等待而提高了传输请求的响应速度（可与CPU并行）。

（3）DMA方式：DMA方式是为了在主存与外设之间实现高速、批量数据交换而设置的，DMA方式比程序控制方式与中断方式都高效（可与CPU并行）。

3、存储设备访问速度：通用寄存器>Cache>内存>硬盘。

4、流水线执行时间=单条指令所需时间+（n-1）*流水线周期(指令分段执行中时间最长的一段)。

5、可靠性：用MTTF/（1+MTTF）来表示。

（1）失效率计算

比如：假设同一型号的1000台计算机，在规定的条件下工作1000小时，其中10台故障。

其失效率λ=10/(1000*1000)=1*10-5

（2）千小时可靠度计算

千小时可靠性R(t)=1-t*λ=1-1000*(1*10-5)=1-0.01=0.99

6、可用性：用MTBF/（1+MTBF）来表示。

7、校验码

（1）奇偶校验：拼接在信息头部，可检奇数位错，不可纠错。

（2）CRC循环冗余校验：拼接在信息尾部，可检错，不可纠错。

（3）海明校验：插入在信息中间，可检错，可纠错。

8、运算符的优先顺序：！>算术运算符>关系运算符>&&>||>赋值运算符。

9、浮点数的运算

（1）阶码的位数决定数的表示范围，位数越多范围越大。

（2）尾数的位数决定数的有效精度，位数越多精度越高。

（3）对阶时，小数向大数看齐，较小数的尾数右移实现。

二 操作系统

1、线程共享的内容包括：进程代码段、进程的公有数据（利用这些共享的数据，线程很容易实现相互之间的通讯）、进程打开的文件描述符、信号的处理器、进程的当前目录、进程用户ID与进程组ID 。

2、线程独有的内容包括：线程ID、寄存器组的值、线程的堆栈（比如，栈指针）、错误返回码、线程的信号屏蔽码。

3、绝对路径从根目录开始的路径，相对路径从当前目录开始的路径。

4、进程的状态

（1）运行：当一个进程在CPU运行时。

（2）就绪：一个进程获得了除CPU外的一切所需资源，一旦得到处理机即可运行。

（3）阻塞：也称等待或睡眠状态，一个进程正在等待某一事件发生而暂时停止运行，此时即使把CPU分配给进程也无法运行。

三 程序设计语言基础

1、解释与编译的区别： （1）解释程序，也称解释器；直接解释执行源程序，或者将源程序翻译成某种中间代码后再加以执行。

（2）编译程序，也称编译器；将源程序翻译成目标语言程序，然后在计算机上运行目标程序。

（3）两者的根本区别：编译方式下，机器上运行的是与源程序等价的目标程序，源程序和编译程序都不再参与目标程序的执行过程，因此执行时效率较高；解释方式下，解释程序和源程序（或某种等价表示）要参与到程序的运行过程中，运行程序的控制权在解释程序，边解释边执行，执行效率较低。即：解释方式，翻译程序不生成独立的目标程序，而编译方式则生成独立保持的目标程序。

2、程序控制结构主要有：顺序结构、选择结构和循环结构。

3、词法分析：非法字符、单词拼写错误。

4、语法分析：标点符号错误、表达式中缺少操作数、括号不匹配等有关语言结构上的错误。

5、静态语义分析：运算符与运算对象类型不合法、取余时用浮点数等错误。

四 数据结构

1、数组与矩阵：

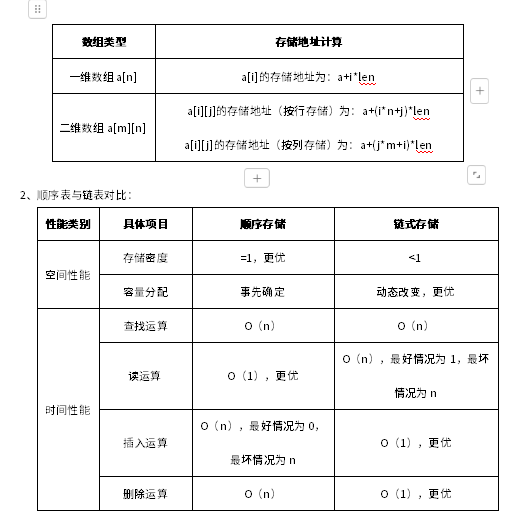
3、循环链表：队空条件：head=tail；队满条件：(tail+1)%size=head。

4、树的概念

（1）双亲、孩子和兄弟：结点的子树的根称为该结点的孩子；相应地，该结点称为其子结点的双亲。具有相同双亲的结点互为兄弟。

（这里涉及到2个层次，第一个层次的子树，这棵子树的根是第一层结点的孩子结点，第一层结点是其子节点的双亲节点/父节点）。

（2）结点的度：一个结点的子树的个数记为该结点的度。

（3）叶子结点：也称为终端结点，指度为0的结点。

（4）内部结点：指度不为0的结点，也称为分支节点或非终端节点。除根结点之外，分支结点也称为内部结点。

（5）结点的层次：根为第一层，根的孩子为第二层，依次类推，若某节点在第i层，则其孩子结点在第i+1层。

（6）树的高度：一棵树的最大层次数记为树的高度（深度）。

5、二叉树的重要特性

（1）在二叉树的第i层上最多有2i-1个结点（i≥1）。

（2）深度为k的二叉树最多有2k -1个结点（k≥1）。

（3）对任何一棵二叉树，如果其叶子结点数为n0，度为2的结点数为n2，则n0=n2+1。

（4）如果对一棵有n个结点的完全二叉树的结点按层序编号（从第1层到⌊log2n⌋+1层，每层从左到右），则对任一结点i（1≤i≤n）有：

如果i=1，则结点i无父结点，是二叉树的根；如果i>1，则父结点是⌊i/2⌋；

如果2i>n，则结点i为叶子结点，无左子结点；否则，其左子结点是结点2i；

如果2i+1>n，则结点i无右子结点，否则，其右子结点是结点2i+1。

6、特殊的树

（1）二叉树：二叉树是每个结点最多有两个孩子的有序树，可以为空树，可以只有一个结点。

（2）满二叉树：任何结点，或者是树叶，或者恰有两棵非空子树。

（3）完全二叉树：最多只有最下面的两层结点的度可以小于2，并且最下面一层的结点全都集中在该层左侧的若干位置。

（4）平衡二叉树：树中任一结点的左右子树高度之差不超过1。

（5）查找二叉树：又称之为排序二叉树。任一结点的权值，大于其左孩子结点，小于其右孩子结点。

（6）线索二叉树：在每个结点中增加两个指针域来存放遍历时得到的前驱和后继信息。

（7）最优二叉树：又称为哈夫曼树，它是一类带权路径长度最短的树。

7、最优二叉树（哈夫曼树）的构造过程：

（1）根据给定的权值集合，找出最小的两个权值，构造一棵子树将这两个权值作为其孩子结点，二者权值之和作为根结点；

（2）在原集合中删除这两个结点的权值，并引入根节点的权值；

（3）重复步骤（1）和步骤（2），直到原权值集合为空。

8、二叉树的遍历：遍历是按某种策略访问树中的每个结点，且仅访问一次的过程。

（1）前序遍历：又称为先序遍历，按根à左à右的顺序进行遍历。

（2）后序遍历：按左à右à根的顺序进行遍历。

（3）中序遍历：按左à根à右的顺序进行遍历。

（4）层次遍历：按层次顺序进行遍历。

......

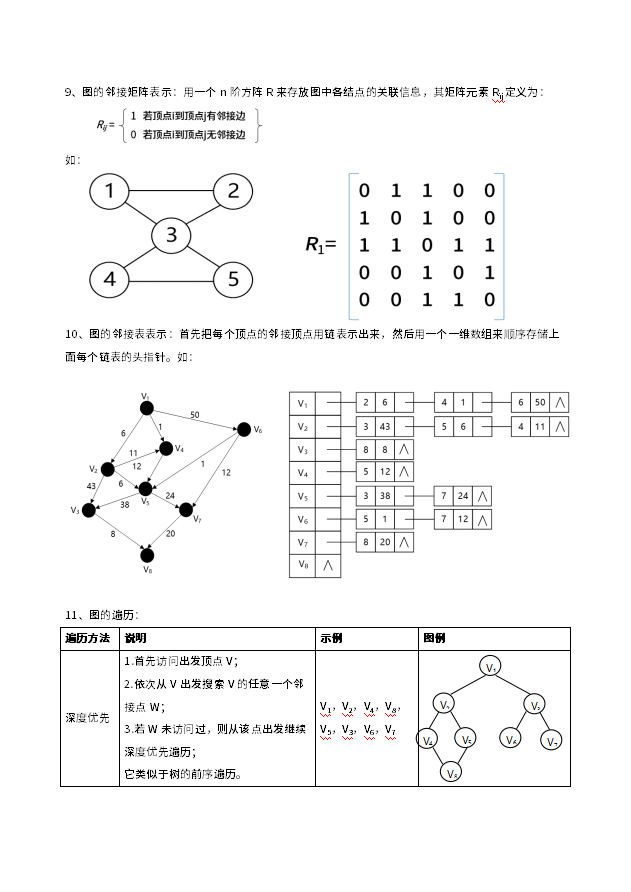
未完