LLC谐振变换器详解（五）| RLC回路频域分析

RLC串联谐振回路

串联RLC电路由一个电阻、一个电容和一个电感串联在一个交流电源上，如图1所示。

图1 串联RLC回路

RLC谐振回路的输入总阻抗的计算式为Zin=XL+XC+R=wL+1/jwC+R，最后化解成下面的这个公式：

wL是感抗的绝对值大小，1/wc是容抗的绝对值大小，在总的输入阻抗中感抗与容抗是可以相互抵消的。

图2  容抗大于感抗示意图

在图2中，感抗与容抗抵消后，还剩下容抗。容抗与纯电阻向量相加，根据平行四边形法则，箭头指的就是最后的阻抗在Y轴的负半轴，所以整个回路的阻抗是呈容性的。

反之感抗与容抗抵消后，还剩下感抗后，整个回路的阻抗是呈感性的，如图3所示。

图3  感抗大于容抗示意图

当串联谐振回路里面的感抗与容抗完全抵消的时候，整个回路的阻抗呈阻性，此时可以计算出来一个频率f0。

XL=XC,即 

在f0这个频率点，电感与电容相对于输入电压来说短路的。因此，R两端电压都等于输入电压Uin。

当输入频率f大于f0这个频率的时候，感抗会变大，而容抗会变小，整个回路呈感性，回路可以等效成电感L与R的串联，如图4所示。频率越大的时候，感抗就越大，而R不变，根据分压原理，UL越大，UR越小。

图4 f>fo等效电路

反之输入频率小于f0的时候，容抗会变大，而感抗会变小，整个回路呈容性，回路可以等效成电感C与R的串联, 如图5所示。频率越小容抗越大，电容电压Uc就越大，UR越小。

图5  f<fo等效电路

综上分析，可以得出一个结论，改变输入的频率f可以改变电阻电压UR，在f0这个频率点的时候，电压最高，且等于输入电压Uin。UR随输入频率变化趋势如图6所示。

图6 电压/频率变化曲线

品质因数

由于整个回路是串联的关系，当输入频率f一定时，UL与Uc电压也是固定的，只要当电阻R变化时，UL与Uc电压才会发生变化。当R增大，回路电流Iin就变小，UL、Uc就小。在谐振电路中，不同负载对应R也是变化的，因此会用品质因数Q（Quality factor）衡量负载变化。

品质因数为储能器件（电感、电容）上储存的功率（无功功率）与电阻R消耗掉的有功功率之比，由于串联的关系，

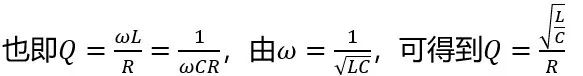
品质因数Q是一个无量纲的数，它影响着谐振电路很多特性，是研究谐振电路时经常要用到的重要参数。这里需要特别强调的是： 在谐振频率f0处，感抗与电阻之比或容抗与电阻之比被称为品质因数Q。

根据谐振回路里面的品质因数Q的计算公式，当L与C设定好后，R越大，说明输出电压越大。如果输出电压恒定，说明负载越轻（R越大），Q越小。

因此，Q的大小代表了输出负载的轻重，Q大负载重，Q小负载就小。在画LLC曲线的时候，不同的Q就代表不同的负载。

增益关系

输出电压与输入电压之比叫增益，一般用G来表示，G=UR/Uin。当频率在f0的时候，最大增益G=1，如图7所示。

图7 频率与增益的关系曲线

在RLC谐振回路里面，当输入频率f=f0的时候，不管R多大，增益G都等于1。如果输入频率不在f0处， R不同的时候增益会不一样。

当频率f>f0，f处在感性区域，也就是感抗抵消容抗后，还剩一些感抗。整个回路可以认为是一个电感串联一个电阻。此时R越小，感抗XL与电阻R之比就越大。这样UR越小。反过来，电阻R越大，UR就越大。

因此可以得出结论，在相同的频率处，电阻R越大，增益就越大。

反过来，当f小于f0的时候，容抗大于感抗，整个回路处于容性区域。当f1固定的时候，容抗是固定的，那电阻越大，分压就越大，这样增益就越大。