递归和回溯

程序小冰

已于 2023-11-01 11:30:47 修改

阅读量143

点赞数 1

分类专栏：数据结构文章标签：数据结构 1024程序员节

于 2023-10-09 11:14:36 首次发布

本文链接：https://blog.youkuaiyun.com/2203_75646004/article/details/133696927

版权

数据结构专栏收录该内容

22 篇文章

订阅专栏

递归

定义

说明：
（1）递归函数求解问题的基本思想是把一个大规模问题的求解归结为一个相对较小规模问题的求解，
小规模归结为小小规模，以此类推，直至问题规模小至边界（边界问题可直接求解）。递归函数由两
部分组成，一部分为递归边界，另一部分为递归关系式。以求阶乘函数为例，递归边界Factorial(1)=1;
递归公式： Factorial(n)=n*Factorial(n-1)，它对应的递归函数如下：
int GetFactorial(int n){
int result;
if(n==1) result = 1; //递归边界，此时问题答案易知，可直接求解
else result =n* GetFactorial(n-1); //递归关系，大问题求解归结为小问题求解
return result;
}

(2)
递归函数设计的核心是寻找递归边界和递归关系。前者相对简单，后者可以采用类似数学归纳法的思想，
假设小规模问题能递归求解（比如问题规模为n-1时f(n-1)能完成求解)，在此基础上考虑如何求解规模为n时如何求解。
若数据对象能拆分为多个部分(比如链表可以拆分为首节点和子链表，子链表比原来的链表小，也可完成递归求解)，
在严格小的子模块上完成递归求解后，之后合并各个子模块的解，得到完整解。

(3) 发生函数递归调用（自己调用自己）或者普通函数调用时，系统需要保存调用发生前的执行场景信息
（包括调用发生前的各个变量取值信息以及函数执行位置等），以便被调函数执行完毕后可以顺利返回并继续执行后续操作。
每次调用都需要保存一个场景信息，保存这些场景信息需要的辅助空间的大小与函数调用的次数呈正比，
或者说其空间复杂度是O(n)，当中n为调用次数。

(4)本例的目的是让学生编写一个递归函数，并在自己的机器上测试递归调用次数达到多少时会发生内存
被爆而出现内存溢出的错误（我办公室机器上设置参数为66000时会溢出）。同样的这个问题，如果不
用递归函数而改用普通的循环语句解决问题，则不会出现内存溢出！

本题要求实现一个递归函数，用户传入非负整型参数n，用户依次输出1到n之间的整数。所谓递归函数就是指自己调用自己的函数。

递归求阶乘

#include<stdio.h>
int f(int n){
    int t,temp;
    if(n==1)
    {
        t=1;//前边界
    }
    else{
        temp=f(n-1);//子问题
        t=temp*n;//当前问题
    }
    return t;
}


int main(){
    int n;
    scanf("%d",&n);
    printf("%d",f(n));
}

#include<stdio.h>
int f(int n){
    int t,temp;
    if(n==1)
    {
        t=1;//前边界
        printf("%d\n",t);
    }
    else{
        t=f(n-1)*n;//当前问题
        printf("%d\n",t);
    }
    return t;
}


int main(){
    int n;
    scanf("%d",&n);
    printf("%d",f(n));
}

5
1
2
6
24
120
120

回溯

回溯算法的框架：

复杂

List<List<Integer>> res = new LinkedList<>();
/* 主函数，输入一组不重复的数字，返回它们的全排列 */
List<List<Integer>> permute(int[] nums) {
    // 记录「路径」
    LinkedList<Integer> track = new LinkedList<>();
    backtrack(nums, track);
    return res;
}
 
// 路径：记录在 track 中
// 选择列表：nums 中不存在于 track 的那些元素
// 结束条件：nums 中的元素全都在 track 中出现
void backtrack(int[] nums, LinkedList<Integer> track) {
    // 触发结束条件
    if (track.size() == nums.length) {
        res.add(new LinkedList(track));
        return;
    }
 
    for (int i = 0; i < nums.length; i++) {
        // 排除不合法的选择
        if (track.contains(nums[i]))
            continue;
        // 做选择
        track.add(nums[i]);
        // 进入下一层决策树
        backtrack(nums, track);
        // 取消选择
        track.removeLast();
    }
}

简单

result = []
def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return
 
    for 选择 in 选择列表:
        做选择
        backtrack(路径, 选择列表)
        撤销选择

例题

7-2先看b站视频后作答输出全排列

分

输入格式:

输入给出正整数n（<10）。

输出格式:

输出1到n的全排列。每种排列占一行，数字间无空格。排列的输出顺序为字典序，即序列a1,a2,⋯,an排在序列b1,b2,⋯,bn之前，如果存在k使得a1=b1,⋯,ak=bk 并且 ak+1<bk+1。

输入样例：

输出样例：

解题步骤：

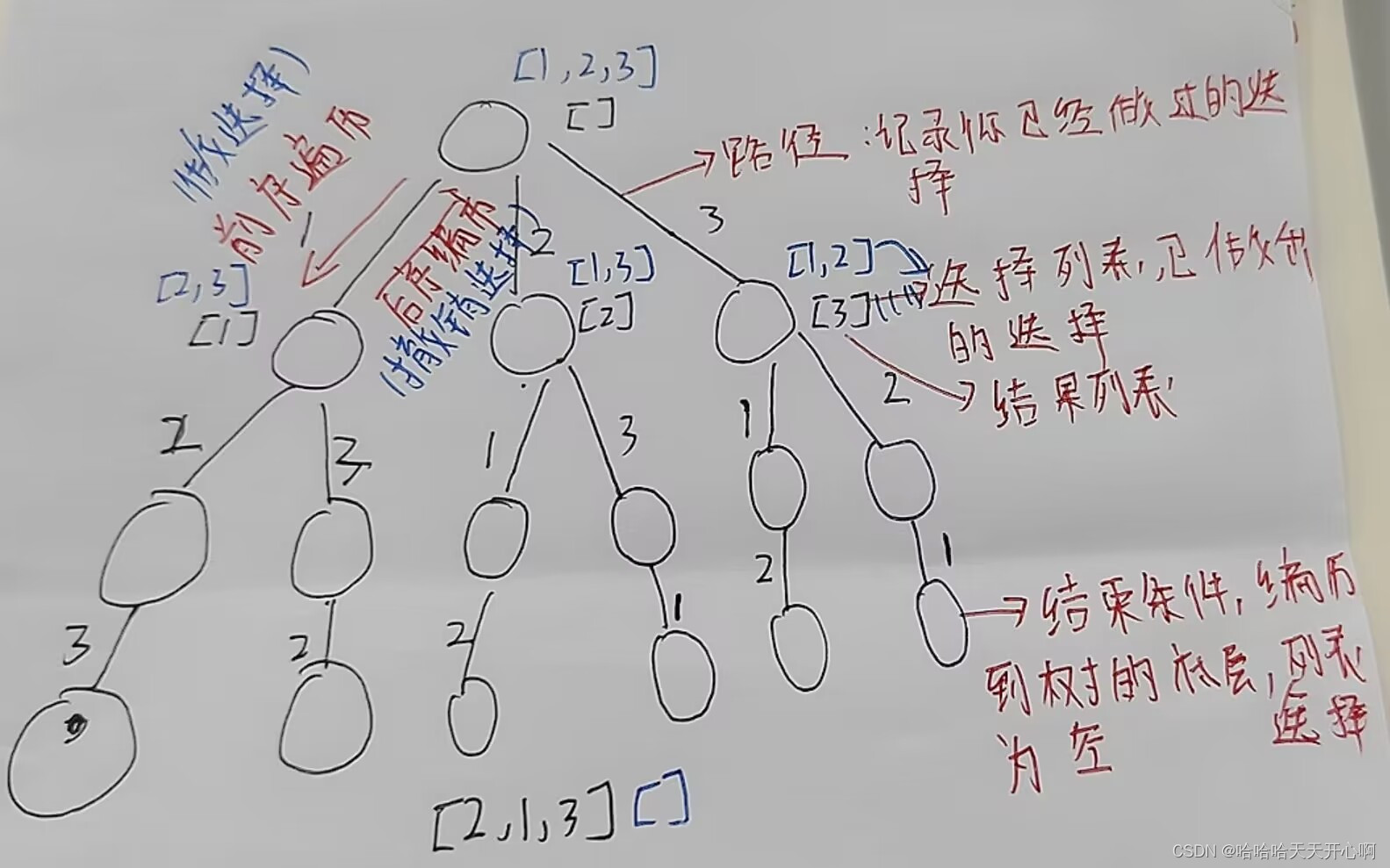
#include<stdio.h>
#define N 30
int n;
int a[100];
int vis[N]= {0};
void dfs(int k)
{


    if(k>n)
    {
        for(int i=1; i<=n; i++)
        {
            printf("%d",a[i]);

        }
printf("\n");

    }
    else
    {
        for(int i=1; i<=n; i++) //从当前已经选择的位置向后选
        {
            if(vis[i]==0)
            {
                vis[i]=1;
                a[k]=i;
                dfs(k+1);
                vis[i]=0;
            }
        }
    }
}
int main()
{
    scanf("%d",&n);
    dfs(1);
    return 0;
}

输入一个数组输出他的全排列

输出一个可重复的全排列

#include<stdio.h>
#define N 30
int n;
int a[100];
void dfs(int k)
{


    if(k>n)
    {
        for(int i=1; i<=n; i++)
        {
            printf("%d",a[i]);

        }
printf("\n");

    }
    else
    {
        for(int i=1; i<=n; i++) //从当前已经选择的位置向后选
        {

                
                a[k]=i;
                dfs(k+1);

        }
    }
}
int main()
{
    scanf("%d",&n);
    dfs(1);
    return 0;
}

6-3先看b站视频后作答求解n皇后问题（递归回溯法）

#include <stdio.h>
#include <stdlib.h>
#define N 20                    //最多皇后个数
int q[N];                        //存放各皇后所在的列号,即(i,q[i])为一个皇后位置

void dispasolution(int n)        //输出n皇后问题的一个解
{
    for (int i=1;i<=n;i++)
        printf("(%d,%d)",i,q[i]);
    printf("\n");
}

bool place(int i,int j)            //测试(i,j)位置能否摆放皇后
{
    if (i==1) return true;        //第一个皇后总是可以放置
    int k=1;
    while (k<i)            //k=1～i-1是已放置了皇后的行
    {    if ((q[k]==j) || (abs(q[k]-j)==abs(i-k)))
            return false;
        k++;
    }
    return true;
}
void queen(int i,int n);

int main()
{    int n;                    //n为存放实际皇后个数
    scanf("%d",&n);
    if (n<=20)
        queen(1,n);                //放置1～i的皇后
    return 0;
}
/* 请在这里填写答案 */
void queen(int i,int n)
{
    if(i>n)
    {
        dispasolution(n);
        return ;
    }
    for(int x=1;x<=n;x++){
        if(place(i,x))
        {
            q[i]=x;
            queen(i+1,n);
            q[i]=0;
        }
    }
}