二叉树 Binary tree

1.树的概念

树是一种非线性的数据结构，它是由n（n>=0）个有限结点组成一个具有层次关系的集合

特点:

有一个特殊的结点，称为根结点，根结点没有前驱结点,除了根节点外,每个节点有且仅有一个父节点, 树是递归定义的,子树之间不能有交集。一颗N个结点的树有N-1条边

结点的度：一个结点含有子树的个数称为该结点的度；

树的度：一棵树中，所有结点度的最大值称为树的度；

叶子结点或终端结点：度为0的结点称为叶结点；

 结点的层次：从根开始定义起，根为第1层，根的子结点为第2层，以此类推

树的高度或深度：树中结点的最大层次；

森林：由m（m>=0）棵互不相交的树组成的集合称为森林

2.二叉树

 二叉树不存在度大于2的结点

 二叉树的子树有左右之分，次序不能颠倒，因此二叉树是有序树

2)两种特殊的二叉树

1. 满二叉树: 一棵二叉树，如果每层的结点数都达到最大值，则这棵二叉树就是满二叉树

 2. 完全二叉树: 完全二叉树是由满二叉树而引出来的,对于深度为K的，有n 个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从0至n-1的结点一一对应时称之为完全二叉树。 满二叉树是一种特殊的完全二叉树

3) 二叉树的性质

1. 若规定根结点的层数为1，则一棵非空二叉树的第i层上最多有2的(i-1)次方 (i>0)个结点

2. 若规定只有根结点的二叉树的深度为1，则深度为K的二叉树的最大结点数是2的k次方-1 (k>=0) 3. 对任何一棵二叉树, 如果其叶结点个数为 n0, 度为2的非叶结点个数为 n2,则有n0＝n2＋1

n0度为0的节点 n1度为1的节点 n2度为2的节点
有N个结点的树有N-1条边 
2*n2+n1=N-1
N=n0+n1+n2
以上两公式推导得:n2+1=n0

 总共有偶数个结点时n1=1,有奇数个结点时n1=0

4. 具有n个结点的完全二叉树的深度k为 log2(n+1)上取整

5. 对于具有n个结点的完全二叉树，如果按照从上至下从左至右的顺序对所有节点从0开始编号，则对于序号为i 的结点有：

若i>0，双亲序号：(i-1)/2；i=0，i为根结点编号，无双亲结点

若2i+1<n,左孩子序号2i+1,否则无左孩子

若2i+2<n,右孩子序号2i+2,否则无右孩子

父亲节点下标为i
左孩子:(2*i)+1
右孩子:(2*i)+2
孩子下标为i
父亲节点下标
(i-1)/2

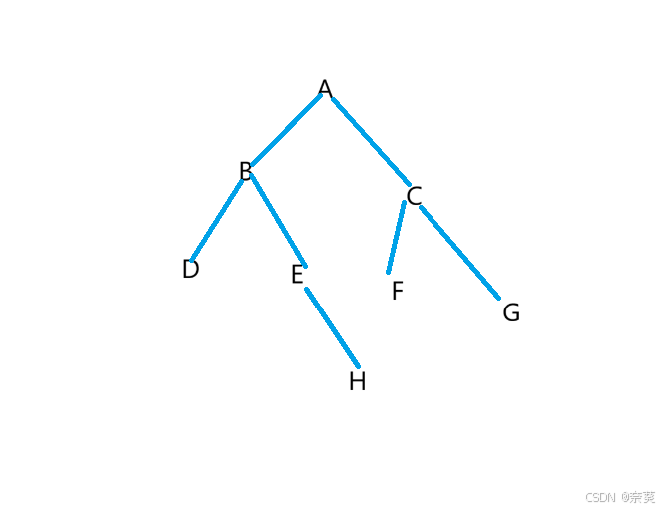
创建一棵简单的二叉树

(孩子表示法)

public class BinaryTree {
    static class TreeNode{
        public char val;
        public TreeNode left;
        public TreeNode right;
        public TreeNode(char val) {
            this.val = val;
        }
    }
    public TreeNode root;//这个引用指向根节点
    //创建一个二叉树
    public TreeNode createTree()

    {
        TreeNode A = new TreeNode('A');
        TreeNode B = new TreeNode('B');
        TreeNode C = new TreeNode('C');
        TreeNode D = new TreeNode('D');
        TreeNode E = new TreeNode('E');
        TreeNode F = new TreeNode('F');
        TreeNode G = new TreeNode('G');
        TreeNode H = new TreeNode('H');
        A.left = B;
        A.right = C; 
        B.left=D;
        B.right=E;
        C.left=F;
        C.right=G;
        E.right=H;
        return A;
    }
}

import com.sun.scenario.effect.impl.sw.sse.SSEBlend_SRC_OUTPeer;

public class Test {
    public static void main(String[] args) {
        BinaryTree binaryTree=new BinaryTree();
        BinaryTree.TreeNode ret= binaryTree.createTree();

    }
}

 

4)二叉树的遍历

NLR：前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点--->根的左子树--->根的右子树。

LNR：中序遍历(Inorder Traversal)——根的左子树--->根节点--->根的右子树。

LRN：后序遍历(Postorder Traversal)——根的左子树--->根的右子树--->根节点。

层序遍历:设二叉树的根节点所在 层数为1，层序遍历就是从所在二叉树的根节点出发，首先访问第一层的树根节点，然后从左到右访问第2层 上的节点，接着是第三层的节点，以此类推，自上而下，自左至右逐层访问树的结点的过程就是层序遍历。

//前序遍历
    public  void  preOrder(TreeNode root){
        if(root==null){
            return;
        }
        System.out.print(root.val+" ");
        preOrder(root.left);
        preOrder(root.right);
    }
    //中序遍历
    public  void  inOrder(TreeNode root){
        if(root==null){
            return;
        }
        inOrder(root.left);
        System.out.print(root.val+" ");
        inOrder(root.right);
    }
    //后序遍历
    public  void  postOrder(TreeNode root){
        if(root==null){
            return;
        }
        postOrder(root.left);
        postOrder(root.right);
        System.out.print(root.val+" ");
    }

import com.sun.scenario.effect.impl.sw.sse.SSEBlend_SRC_OUTPeer;

public class Test {
    public static void main(String[] args) {
        BinaryTree binaryTree=new BinaryTree();
        BinaryTree.TreeNode root= binaryTree.createTree();

        binaryTree.preOrder(root);
        System.out.println();
        binaryTree.inOrder(root);
        System.out.println();
        binaryTree.postOrder(root);
    }
}

//前序遍历
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> ret=new ArrayList<>();
        if(root==null) return ret;
        ret.add(root.val);
        List<Integer>leftTree=preorderTraversal(root.left);//合理利用函数的返回值
        ret.addAll(leftTree);
        List<Integer>rightTree=preorderTraversal(root.right);
        ret.addAll(rightTree);
        return ret;
    }
}
//中序
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> ret=new ArrayList<>();
        if(root==null) return ret;
        
        List<Integer>leftTree=inorderTraversal(root.left);
        ret.addAll(leftTree);
        ret.add(root.val);
        List<Integer>rightTree=inorderTraversal(root.right);
        ret.addAll(rightTree);
        return ret;
    }
}
//后序
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> ret=new ArrayList<>();
        if(root==null) return ret;
        List<Integer>leftTree=postorderTraversal(root.left);
        ret.addAll(leftTree);
        List<Integer>rightTree=postorderTraversal(root.right);
        ret.addAll(rightTree);
        ret.add(root.val);
        return ret;
    }
}

使用 addAll()，表示把一个集合的所有元素加进去

List<Integer> list1 = new ArrayList<>();
list1.add(1);
list1.add(2);

List<Integer> list2 = new ArrayList<>();
list2.add(3);

list2.addAll(list1);  // list2 变成 [3, 1, 2]

为什么在下面这段代码中：

if (root == null) {
    return ret;
}

要返回一个空的列表 ret，而不是返回 null？

if (root == null) {
    return null;
}

---

✅ 正确写法为什么是返回空列表 ret？

List<Integer> ret = new ArrayList<>();
if (root == null) {
    return ret;
}

原因一：为了保持递归结构的统一性

这段代码是使用递归来实现二叉树的中序遍历（左 → 根 → 右）：

List<Integer> leftTree = inorderTraversal(root.left);
ret.addAll(leftTree);  // 把左子树的结果加进来
ret.add(root.val);     // 把当前节点加进来
List<Integer> rightTree = inorderTraversal(root.right);
ret.addAll(rightTree); // 把右子树的结果加进来

• leftTree 和 rightTree 都是 List<Integer> 类型；
• 所以无论递归到哪个节点，我们都希望它们返回的是一个空列表而不是 null；
• 如果返回 null，后面调用 addAll(leftTree) 就会抛出 NullPointerException！

---

原因二：避免空指针异常

如果你写成：

if (root == null) {
    return null;
}

那么在父节点调用时：

List<Integer> leftTree = inorderTraversal(root.left);
ret.addAll(leftTree);  // ❌ NullPointerException！

如果 leftTree == null，调用 addAll(null) 就会抛出异常：

java.lang.NullPointerException: Cannot invoke "java.util.Collection.toArray()" because "c" is null

---

✅ 所以正确写法是：

List<Integer> ret = new ArrayList<>();
if (root == null) {
    return ret; // 返回一个空列表，而不是 null
}

这样：

• 保证每次递归都返回一个有效的 List 对象；
• 即使是空列表，也可以安全地调用 addAll()；
• 结构统一，逻辑清晰，不易出错。