本文详细解析了全排列（包括重复元素）和组合问题的解决方案，主要使用回溯法，通过两种编码策略（基于交换和标记数组）来实现。文章通过具体示例和代码解释了如何填充排列和组合，特别讨论了处理重复元素的关键步骤，适用于解决LeetCode上的相关问题。
2021年11月5号参加了抖音电商后端研发的实习面试（一面）。面试时候的状态：leetcode刷题不到50，八股文没看，20年8月辞职考研到现在开学2个多月（中间差不多一年时间）没做过项目，之前的项目中的很多细节没回顾。基本来说一面已凉~
面试过程中考察的算法题目：全排列（比较简单，可我不会，大学期间打的肯定是个假ACM），我不配，真的！[狗头]
本文主要是介绍了使用回溯法来解决排列组合问题。
文章目录
一、全排列问题（数字不可重复 leetcode-46）
1. 题目描述
给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
示例 1：
输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2：
输入：nums = [0,1]
输出：[[0,1],[1,0]]
示例 3：
输入：nums = [1]
输出：[[1]]
2. 解题思路
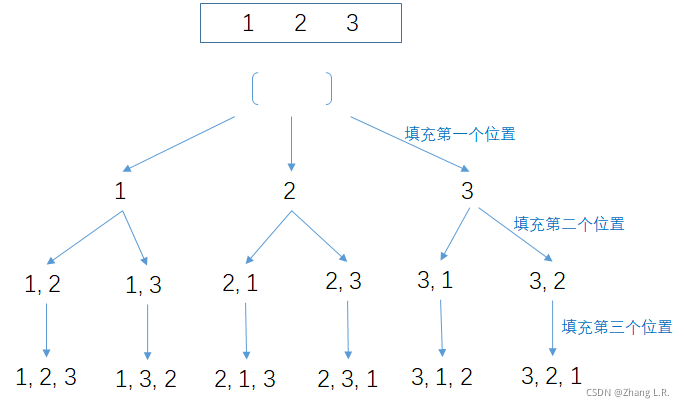
假设以
[
1
,
2
,
3
]
[1,2,3]
[1,2,3] 这种排列顺序为例，第一个位置填好元素之后(序列变为
[
1
,
x
,
x
]
[1, x ,x ]
[1,x,x])，那么接下来该填充第二个位置的元素，由于元素
1
1
1 已经用过了，那么只能从接下来的
2
,
3
2,3
2,3 中选择一个元素填充到集合中（序列变为
[
1
,
2
,
x
]
[1, 2 ,x ]
[1,2,x]），那么在最后一次，需要填充第三个位置的元素的时候，再将
3
3
3 填入到排列中即可（得到序列
[
1
,
2
,
3
]
[1, 2 ,3 ]
[1,2,3]）。
此时，需要回溯到 [ 1 , 2 , x ] [1, 2 ,x ] [1,2,x]处，发现仅存的3已经遍历了一次，那么将再次回溯到 [ 1 , x , x ] [1, x ,x ] [1,x,x]状态。因为上一次排列中，第二个位置的元素使用了2来填充，那么此时使用3来填充第二个元素（得到序列 [ 1 , 3 , x ] [1, 3 ,x ] [1,3,x]）。再递归填充第三个元素，即得到序列 [ 1 , 3 , 2 ] [1, 3, 2] [1,3,2]
填充第一个位置的时候，我们是从全部n个序列中任意选择一元素 k k k 来填充。那么填充第二个元素的时候，我们则要在除了元素 k k k 之外的全部n-1个序列中再任意选择一个元素。最终，当得到的结果序列长度是n的时候，得到一个结果集序列。那么此时就有两种方案来标记元素k是否已经被选择：（1）使用标记数组，每次将某个元素填充到第cur处的时候，判断该元素是否已经被使用过。（2）在给定的数组元素中进行交换，将某个元素填充到结果集的第cur个位置的时候，将该元素与cur处的元素交换，下次再选择的时候，只在cur之后的n-cur个元素中选择。
因此就有两种编码方案：
3. 代码
编码方案1：基于交换的方案
假设程序进行到第某次递归的时候，dfs传入的参数为：nums=
[
3
,
2
,
1
,
4
,
5
]
[3, 2, 1, 4, 5]
[3,2,1,4,5]，cur=2（表示此次需要填充第2个位置的元素），res=[3, 2]，len=5 。cur=2即在nums数组的下标区间
[
2
,
n
)
[2, n)
[2,n) 中选择一个元素填充到第cur处。此时因为i=cur，那么就会将元素1填充到cur处（此时res=[3, 2, 1]），程序继续调用dfs函数以填充第cur+1个位置。
当递归结束并回溯到cur=2的时候，之前的交换等都需要还原成原来的顺序（即
[
3
,
2
,
1
,
4
,
5
]
[3, 2, 1, 4, 5]
[3,2,1,4,5]），循环中的 i+1， 即从
[
3
,
n
)
[3, n)
[3,n) 中选择一个元素填充到cur处，此时将nums[i=3] 和 nuns[cur=2]交换位置，即将nums[3]填充到了 cur = 2 处，此时res=[3, 2, 4]
简而言之，nums=
[
3
,
2
,
1
,
4
,
5
]
[3, 2, 1, 4, 5]
[3,2,1,4,5]中，填充第cur=2处的元素的时候，nums的前2个元素就是排好的元素，而后边的3个元素为待排列的元素，其结构如下：
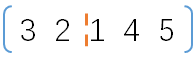
此时要填充第cur=2的元素，需要在[1, 4, 5]中任选一个，使之与nums[cur]交换位置（比如在[1, 4, 5]中选择了4），那么此时nums=
[
3
,
2
,
4
,
1
,
5
]
[3, 2, 4, 1, 5]
[3,2,4,1,5]，此时nums的前3个元素（[3, 2 4]）就是排好的元素，而后边的2个元素（[1, 5]）为待排列的元素。
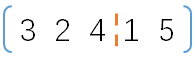
public List<List<Integer>> permute(int[] nums) {
// 存储结果
List<List<Integer>> res = new ArrayList();
// 数组的长度
int len = nums.length;
// 从第 0 个位置开始填
dfs(Arrays.stream(nums).boxed().collect(Collectors.toList()), 0, len, res);
return res;
}
/**
* 表示将元素填充到cur处
* @param nums 给定的待排列数组
* @param cur 当前需要填充的位置
* @param len 数组的长度
* @param res 结果集
*/
public void dfs(List<Integer> nums, int cur, int len, List<List<Integer>> res) {
// 递归的结束条件：当cur等于len-1的时候，表示已经填到了末尾了，此时将结果记录下来
if (cur == len - 1) {
res.add(new ArrayList(nums));
return;
}
for (int i = cur; i < len; i++) {
// 交换之后，表示使用nums数组的第i个位置的元素填充某种排列的第cur个位置(将第i和第cur位置的元素互换)
Collections.swap(nums, i, cur);
// 接下来就递归的填充某排列的第cur+1位置
dfs(nums, cur+1, len, res);
// 回溯，即换回原来的排列顺序
Collections.swap(nums, i, cur);
}
}
编码方案2：基于标记数组的方案
不需要在nums数组中交换数据，只需要使用一个标记数组vis来记录某个元素是否被使用过即可。每次递归需要遍历整个nums数组，以找到未被标记过的元素。
public List<List<Integer>> permute(int[] nums) {
// 存储结果
List<List<Integer>> res = new ArrayList();
// 数组的长度
int len = nums.length;
// 标记数组：记录第i个元素是否被访问过
boolean[] vis = new boolean[len];
// 记录已排好的序列
Deque<Integer> path = new ArrayDeque<>();
// 从第 0 个位置开始填
dfs(Arrays.stream(nums).boxed().collect(Collectors.toList()), 0, len, res, vis, path);
return res;
}
/**
* 表示填充第cur个元素
* @param nums
* @param cur
* @param len
* @param res
* @param vis
* @param path
*/
public void dfs(List<Integer> nums, int cur, int len, List<List<Integer>> res, boolean[] vis, Deque<Integer> path) {
// 递归结束的条件: 已排好的序列长度与nums数组长度相同的时候，表示该排列已完成，需要返回并回溯
if (path.size() == len) {
res.add(new ArrayList<>(path));
return;
}
// 循环，每次从nums中选择一个未使用的元素填充到path中
for (int i = 0; i < len; i++) {
// 判断nums[i]元素是否被访问过, 如果被访问过，跳过并检查下一个元素，直到找到一个未被访问的元素
if (vis[i]) {
continue;
}
// 找到一个未被访问过的元素后，将其放入到path中，并将该位置的元素标记为已访问过
path.addLast(nums.get(i));
vis[i] = true;
// 再次填充第cur+1个元素
dfs(nums, cur + 1, len, res, vis, path);
// 递归返回的时候，需要之前的标记清楚，并从结果子集中剔除
vis[i] = false;
path.removeLast();
}
}
二、全排列问题（数字可重复 leetcode-47）
1. 题目描述
给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。
示例 1：
输入：nums = [1,1,2]
输出：
[[1,1,2],
[1,2,1],
[2,1,1]]
示例 2：
输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
提示：
1 <= nums.length <= 8
-10 <= nums[i] <= 10
2. 解题思路
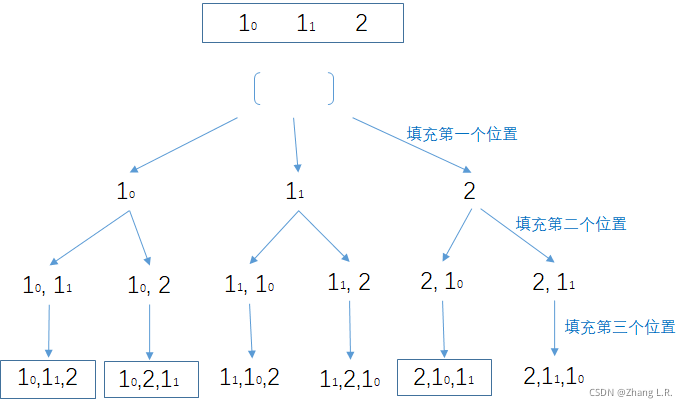
与上边类似，使用标记数组的方案来解决该问题。那么与一个题目不同的地方就是，我们需要排除掉那些重复的排列，只保留不重复的排列。
看上图，我将重复的元素
1
1
1根据其下标进行了标记，最终的结果中，我们只需要保留重复元素的下标顺序是递增的即可（如：
[
1
0
,
1
1
,
2
]
，
[
1
0
,
2
,
1
1
]
，
[
2
,
1
0
,
1
1
]
[1_0, 1_1, 2]，[1_0, 2, 1_1]，[2, 1_0, 1_1]
[10,11,2]，[10,2,11]，[2,10,11]）。那么，在每次选择元素放入path数组的时候，需要进行如下判断：
if (vis[i] || ( i > 0 && nums[i] == nums[i-1] && !vis[i-1])) {
continue;
}
解释上述代码即：
（1）当nums数组中第i个元素访问过的话，跳过后边的操作，并继续选择下一个元素。
（2）当nums数组中第i个元素与其前边的第i-1个元素相同，且前边的元素未被访问过的话，也将跳过后边的操作。
关于第二个判断条件，简而言之即：如果重复元素的前一个元素被访问过了，那么后边的重复元素可以被访问，但如果前一个重复的元素未被访问过，那么其后边的都不可以被访问。
举个例子来说明一下条件（2）：
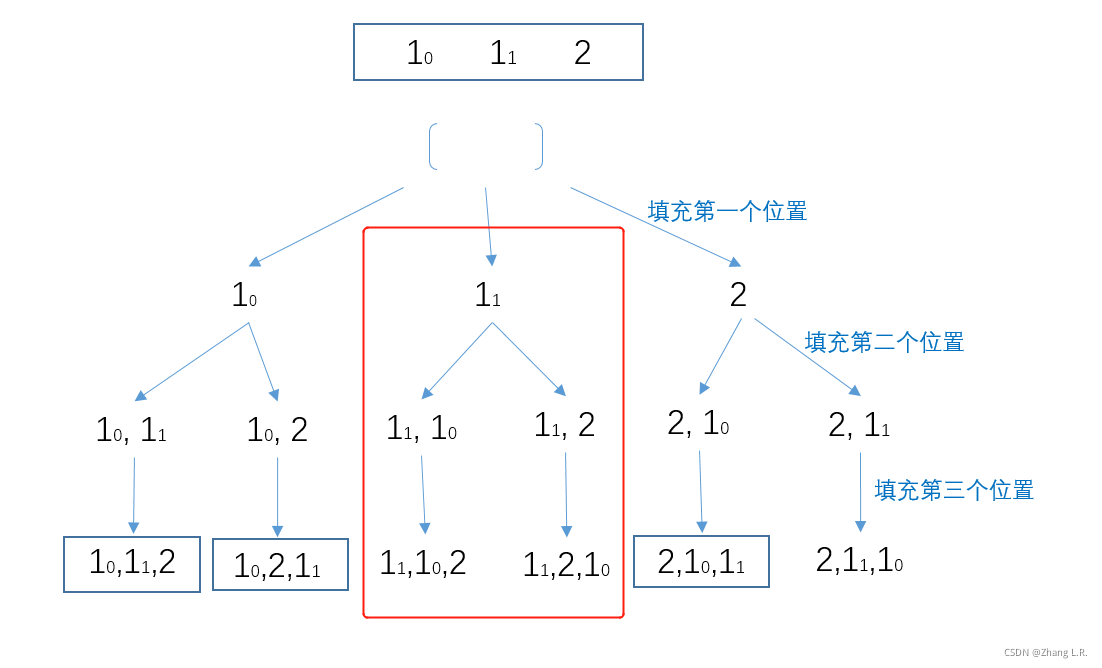
当第一次调用递归填充第一个位置的时候（cur=1）的时候，会先将
1
0
1_0
10放入结果集中，此时
v
i
s
=
[
t
r
u
e
,
f
a
l
s
e
,
f
a
l
s
e
]
vis=[true, false, false]
vis=[true,false,false]。然后递归填充第二个位置的元素（cur=2），这时for循环从0到n，因为vis[0] = true， 跳过后边的操作；i=1的时候，因为(i > 0 && nums[i] == nums[i-1] && !vis[i-1]))中
!
v
i
d
[
0
]
!vid[0]
!vid[0] 返回的是
f
a
l
s
e
false
false 那么，nums[1] 也将放入到path结果集中。此时，结果集中为
[
1
0
,
1
1
,
x
]
[1_0, 1_1, x]
[10,11,x]。
但当递归要进行到上图的红框内的时候，此时
v
i
s
=
[
f
a
l
s
e
,
f
a
l
s
e
,
f
a
l
s
e
]
vis = [false, false, false]
vis=[false,false,false]， 因此在程序想要将nums[i=1]即元素
[
1
1
]
[1_1]
[11] 放入到path结果集的第一个位置的时候，由于i > 0 && nums[i] == nums[i-1] && !vis[i-1]，可知
1
0
1_0
10 元素并未放入到结果集中，那么跳过循环下边的操作，直接执行下一个递归树。即：
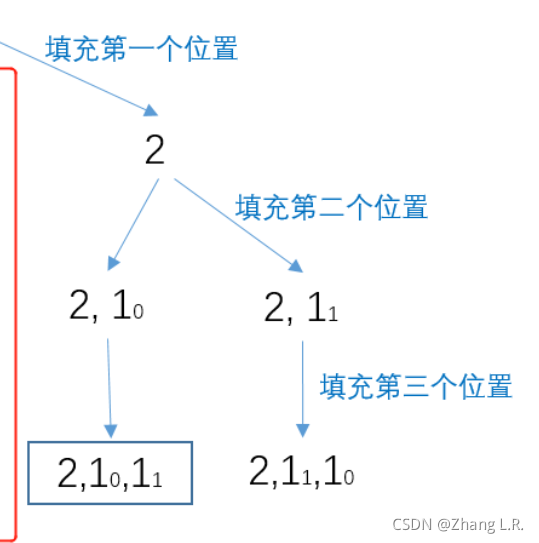
上边的解决方案的前提是：nums数组中重复元素都排列在一起。因此，只需要对给定的nums数组进行一次递增排序就行了。
到此，我们就清楚了解决重复元素的全排列问题的核心难题，下边就是代码实现啦~
3. 代码
public List<List<Integer>> permuteUnique(int[] nums) {
// 存储结果
List<List<Integer>> res = new ArrayList();
// 数组的长度
int len = nums.length;
// 标记数组：记录第i个元素是否被访问过
boolean[] vis = new boolean[len];
// 记录已排好的序列
Deque<Integer> path = new ArrayDeque<>();
Arrays.sort(nums);
// 从第 0 个位置开始填
dfs(Arrays.stream(nums).boxed().collect(Collectors.toList()), 0, len, res, vis, path);
return res;
}
/**
* 表示填充第cur个元素
* @param nums
* @param cur
* @param len
* @param res
* @param vis
* @param path
*/
public void dfs(List<Integer> nums, int cur, int len, List<List<Integer>> res, boolean[] vis, Deque<Integer> path) {
// 递归结束的条件: 已排好的序列长度与nums数组长度相同的时候，表示该排列已完成，需要返回并回溯
if (path.size() == len) {
res.add(new ArrayList<>(path));
return;
}
// 循环，每次从nums中选择一个未使用的元素填充到path中
for (int i = 0; i < len; i++) {
// 判断nums[i]元素是否被访问过, 如果被访问过，跳过并检查下一个元素，直到找到一个未被访问的元素
if (vis[i] || (i > 0 && nums.get(i).equals(nums.get(i-1))) && !vis[i-1]) {
continue;
}
// 找到一个未被访问过的元素后，将其放入到path中，并将该位置的元素标记为已访问过
path.addLast(nums.get(i));
vis[i] = true;
// 再次填充第cur+1个元素
dfs(nums, cur + 1, len, res, vis, path);
// 递归返回的时候，需要之前的标记清楚，并从结果子集中剔除
vis[i] = false;
path.removeLast();
}
}
三、组合问题（leetcode-77）
1. 题目描述
给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。你可以按 任何顺序 返回答案。
示例 1：
输入：n = 4, k = 2
输出：
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
示例 2：
输入：n = 1, k = 1
输出：[[1]]
提示：
1 <= n <= 20
1 <= k <= n
2. 解题思路
结合无重复的全排列问题，这个问题就是在全排列的基础上进行了一些变动。以示例1为例。
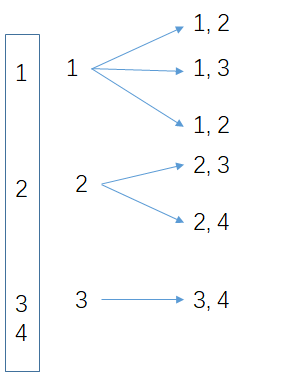
当用nums数组中的第i个元素去填充结果集（path）的第1个位置的时候，那么结果集（path）的第二个位置的元素必使用nums数组中第i个元素后边的任意一个元素来填充。那么使用for循环来从nums数组中取第i个元素以填充到结果集（path）的第一个元素。并通过递归调用dfs函数，在
[
i
+
1
,
n
)
[i+1, n)
[i+1,n) 中任取一个元素，并填充到结果集（path）的下一个待填充位置。
3. 代码
public List<List<Integer>> combine(int n, int k) {
// 返回的结果集
List<List<Integer>> res = new ArrayList<>();
// 记录结果集中的一个排列（组合顺序）
Deque<Integer> path = new ArrayDeque<>();
// 这里的cur不是代表数组的坐标了，而是代表要填充的数值
dfs(n, k, 1, res, path);
return res;
}
/**
*
* @param n 元素个数 [1, n]
* @param k 子集的个数 k <= n
* @param cur 当前需要向结果集的单个排列中填充第cur个元素
* @param res 需要返回的结果总集
* @param path 记录结果集的单个排列
*/
private void dfs(int n, int k, int cur, List<List<Integer>> res, Deque<Integer> path) {
if (path.size() == k) {
res.add(new ArrayList<>(path));
return;
}
// 从 [1, n] 中遍历，将未访问过的数字放入到path中
for (int i = cur; i <= n; i++) {
path.addLast(i);
// 调用递归填充path中下一个位置的元素， （使用 nums 数组中 i 后边的元素来填充，故将i+1作为参数传递给递归函数）
dfs(n, k, i + 1, res, path);
path.removeLast();
}
}
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
