深度学习笔记2

在表达式中，我们通常用方括号表示层数，而用圆括号表示单独的训练量

神经网络的图从左往右依次为：输入层【0】（一般不作正式层）；隐藏层【1】；输出层【2】；输出

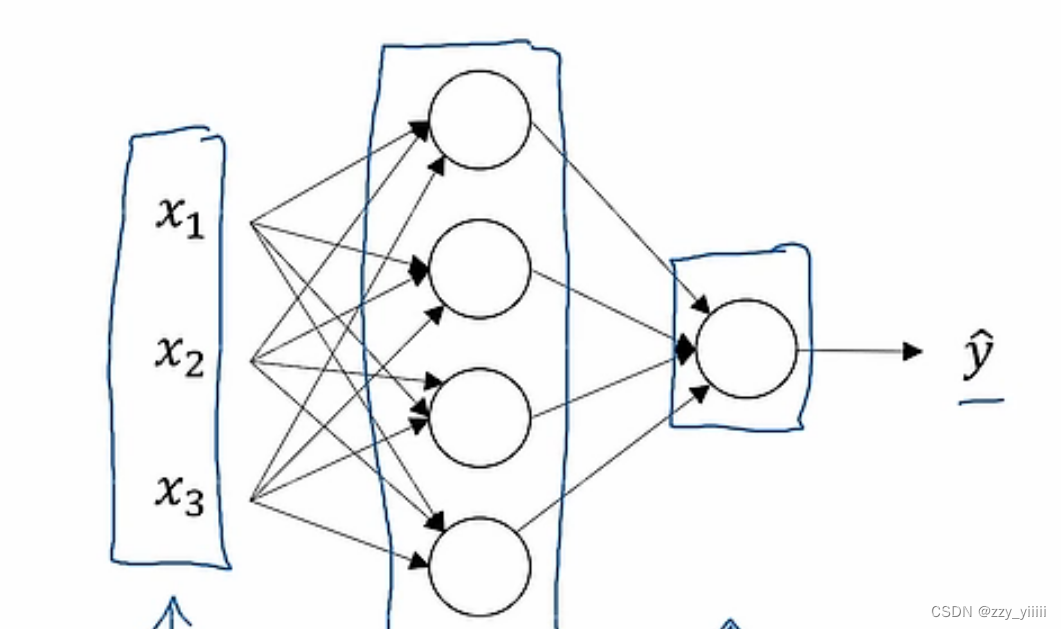
激活函数：将线性函数转化为非线性函数；并且将范围框定在0-1之间。

对于二元分类，sigmoid函数更为合适，而对于其他种类的分类则更多选择relu函数（更多选择）或者tanh函数

（从上到下依次为Tanh函数和RelU函数）

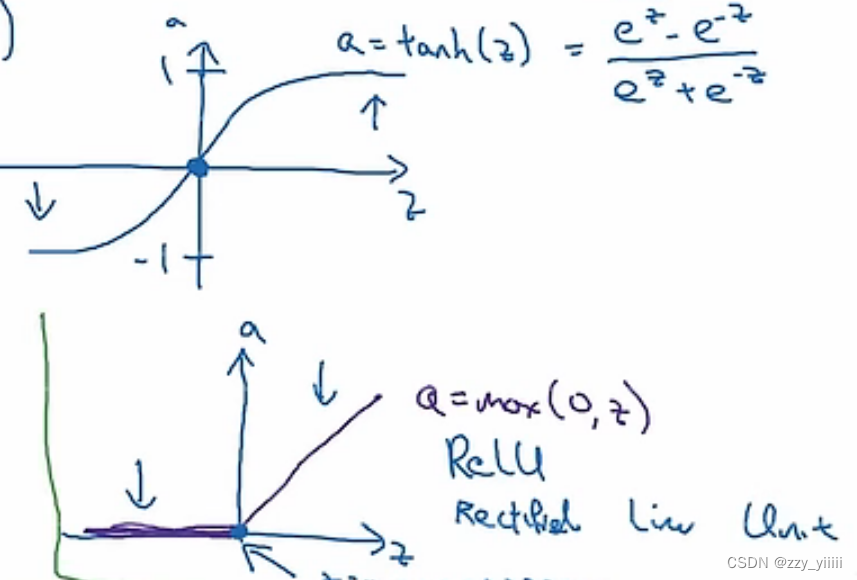
leaky RelU函数 a=max（0.01z，z）

如果使用线性激活函数，那么神经网络的深层也就没有了意义，因为输入和输出之间可以整合为一个式子。但是如果输出的是一个实数，而不是类似与0或1的判断值，那么就可以用线性激活函数（恒等激活函数）。至少隐藏层不应使用线性激活。

初始化w变量不能全设为0，因为这样会导致依照该变量计算的值完全相等，没有任何区别，这样就没有了计算的意义。这种情况称为对称失效。

这样设置 w的初始值可以更好的使激活函数发挥作用，以免产生因步长过大而导致的激活函数效果不明显的后果。0.01适合浅层的神经网络。

计算交叉熵成本时可以不用循环就可以算出答案

logprobs = np.multiply(np.log(A2),Y)
cost = - np.sum(logprobs)                # 不需要使用循环就可以直接算出来。

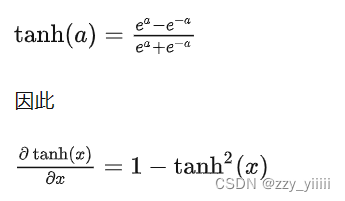
 在两层的神经网络中这个求导公式可以解决连接问题

前一半是对整个结构的求导，而后一半是对自身的求导。