机器学习是人工智能的子集,而通常的机器学习分为3类:
1.监督学习
数据通过某些特定算法和模型的计算从而得出一个目标函数,同时还有一个标准答案对这个目标函数进行验证,以检测这个目标是否符合预期。
2.非监督学习
基本与上类学习方式相同,唯一的不同在于,他没有标准答案,只有通过一些间接的方法对答案进行验证,较上种方法困难。
3.强化学习
与监督类学习有很大的不同,它有状态和环境的响应组成,反馈来自于响应,通过响应来判断这个模型的契合程度,当响应不断符合预期,模型也就越好。
监督学习的要素:模型,数据,目标函数,优化算法
一层神经网络可视化
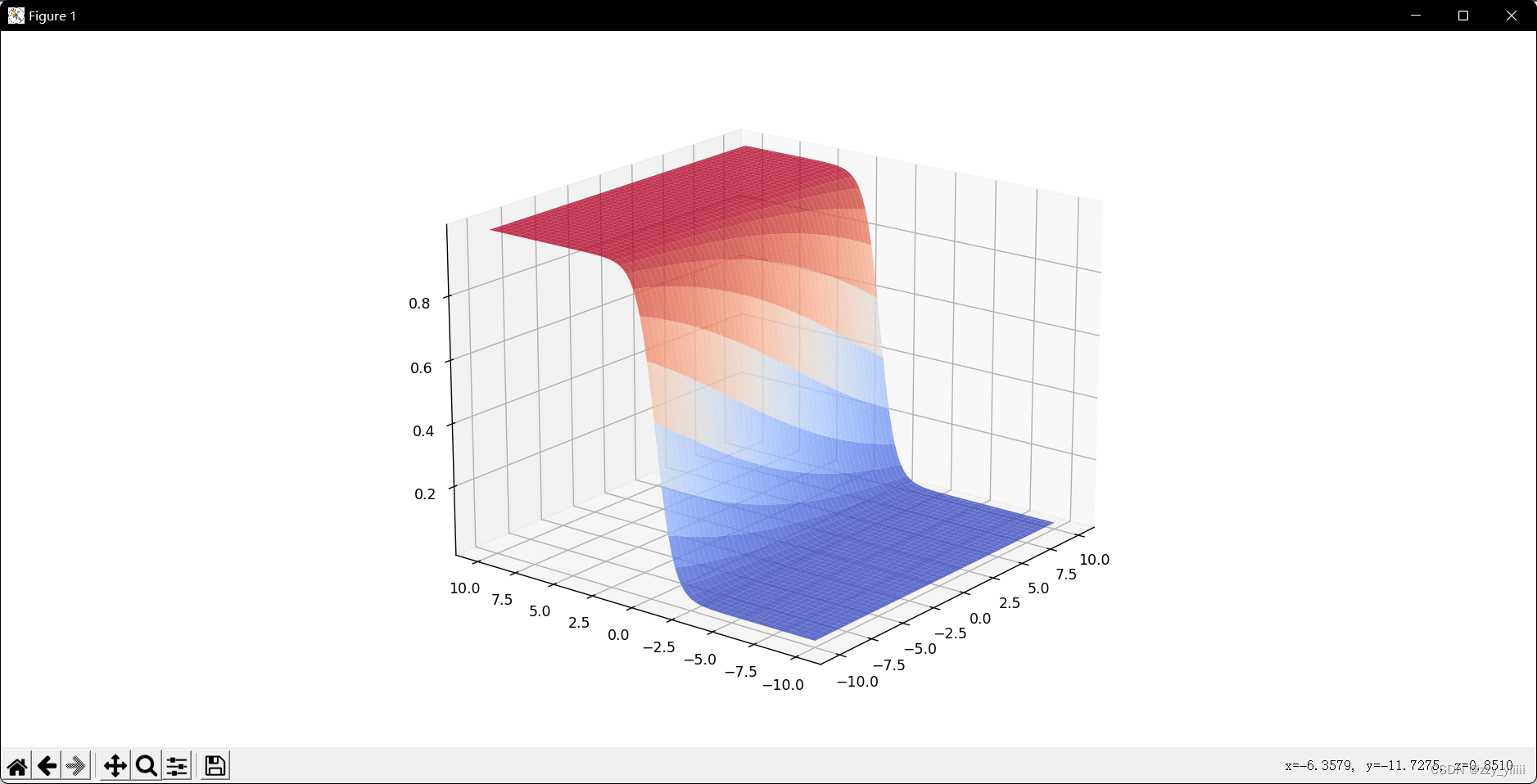
import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
class FC:
def __init__(self, in_num, out_num, lr=0.01):
self._in_num = in_num
self._out_num = out_num
self.w = np.random.randn(out_num, in_num) * np.sqrt(2 / in_num)
self.b = np.random.randn(out_num) * np.sqrt(2 / in_num)
def sigmoid(self, x):
return 1 / (1 + np.exp(-x))
def forward(self, x):
z = np.dot(self.w, x) + self.b
y = self.sigmoid(z)
return y
def draw3D(X, Y, Z):
fig = plt.figure(figsize=(15,7))
ax = Axes3D(fig)
ax.view_init(30, 45)
ax.plot_surface(X, Y, Z, rstride=2, cstride=2, cmap=plt.cm.coolwarm,alpha=0.8) # 提高rstride和cstride的值
plt.show()
x = np.linspace(-10, 10, 100)
y = np.linspace(-10, 10, 100)
X, Y = np.meshgrid(x, y)
data = np.column_stack((X.flatten(), Y.flatten()))
fc = FC(2, 1)
Z1 = fc.forward(data.T)
Z1 = Z1.reshape(100, 100)
draw3D(X, Y, Z1)
线性回归(二分类)
何为二分类,即分类结果只有两个,可以理解为对或错
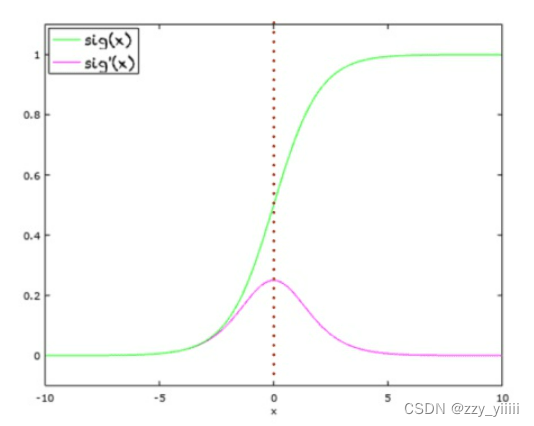
首先,要有输入(可以多个,也叫做特征值)和一个输出,先对这些特征值进行矩阵(向量)运算,从而体现出不同的特征值所体现出的权重,然后设特征值为x,权重函数为w,还有一个偏移量b,得到的结果为w*x+b,但是这个结果可大可小,无法框定在一个特定的范围内,所以要将结果带入一个非线性函数sigmoid函数(如下图的绿色部分,红色为其导数)里。这样可以保证得到的结果在0—1之间。(非线性函数的种类有很多,还有tanh函数等等)
得到了结果还要计算其中的损失函数, 从而分析运算的结果是否能够满足自己预期,即监督学习,损失函数也有很多种,常见的有如下:均方误差损失函数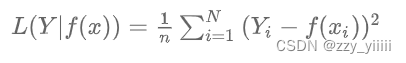
代价函数: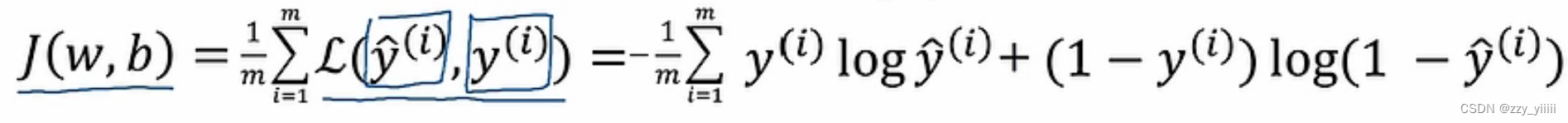
这个函数很有意思,当真实值(y(i))为0时 只有当y帽尽可能接近0时,损失函数才会小;当(y(i))为1时,只有当y帽尽可能接近1时损失函数才会小,这很好地符合了我们的预期。
然而,如何才能使得代价函数尽可能的小呢?
答案是使用梯度下降算法,(何为梯度,简单解释,在一个三维坐标系xyz中,函数分别关于x和y求偏导数,再将两个偏导数进行向量加法变成一个偏导,借用这个导数,就可以找到这个代价函数最低的点!)
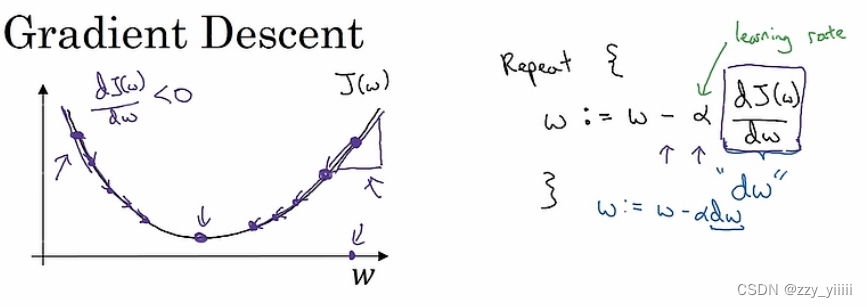
右边的公式可以很好地解释简单的梯度下降法,这里不考虑b的偏移,α为学习率,可以很好的决定每一次位移的长度,而再右边的是有关w的导数,通过不断的循环可以得到函数的最低值。
反向传播:就是一个求输出对输入的偏导的过程,虽然在过程中可能会有多部函数,不过用链式法则可以解决。

最后求出L函数关于w1的导数就是上文的“dw”。
代码:
在代码中我们需要一次次的循环来达到找到适合的特征函数,但同时循环在较大的数据集中的极其低效的,我们可以通过向量化来提高效率。(尽量避免使用显式的for循环)
假设w和x为两个矩阵,在无矢量的实现中,我们要一一对应的相乘,但用了矢量化的计算就可以一步到位,在我看来,这是numpy库中函数的特点吧。用np.dot(w,x)可以快速将两个函数矩阵相乘。通过下图,我们可以很明显的看出矢量化计算能极大提高运算效率,其底层原理是运用CPU的并行化来使得运算效率提高。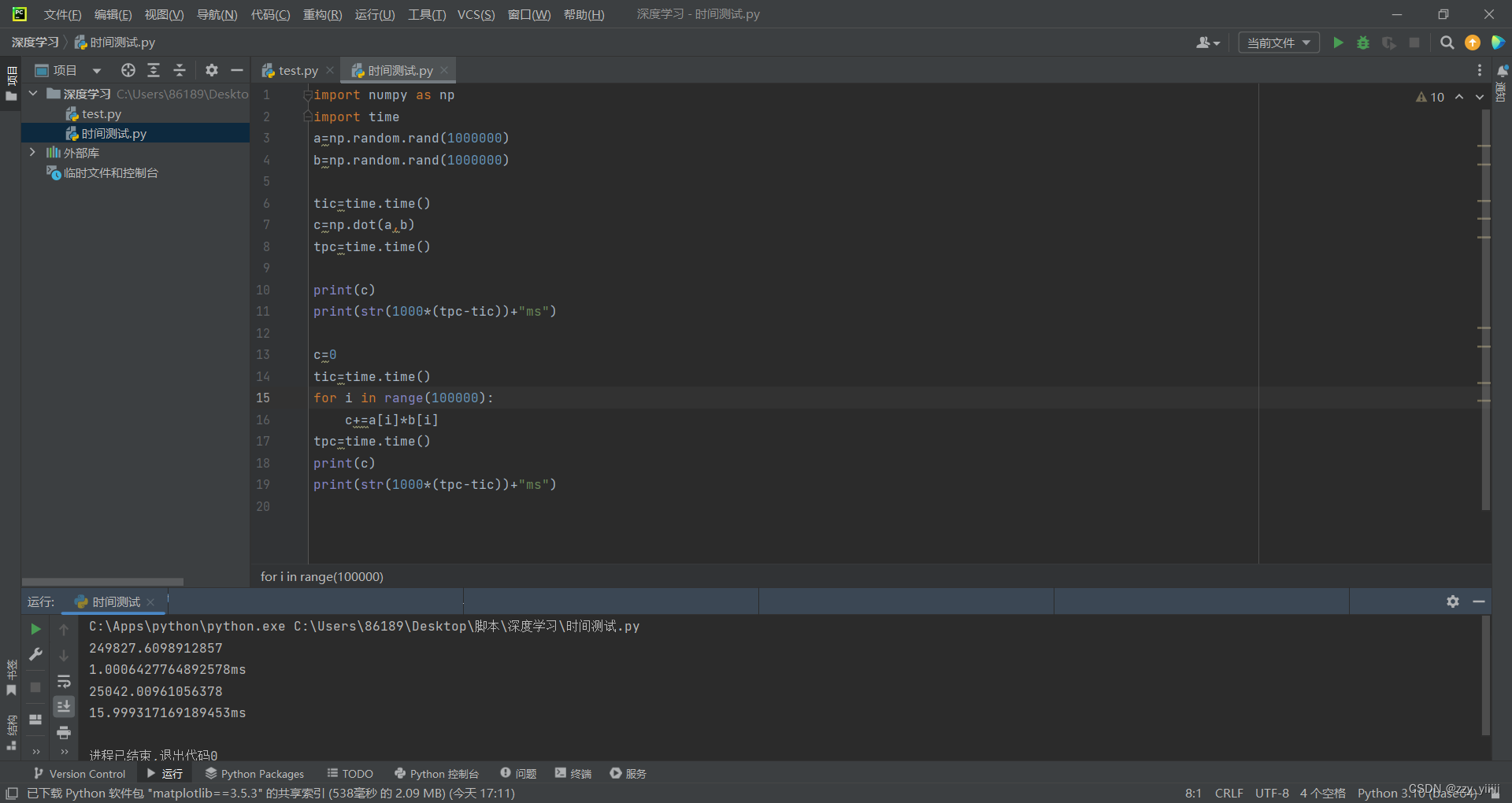
这里还要介绍numpy中的一种矩阵计算方法:广播,广播有以下规则
规则1:如果两个数组的维度不相同,那么小维度数组的形状将会在最左边补1.
规则2:如果两个数组的形状在任何一个维度上都不匹配,那么数组的形状会沿着维度为1的维度拓展以匹配另外一个数组形状。
规则3:如果两个数组的形状在任何一个维度上都不匹配并且没有任何一个维度等于1,那么会引发异常。
代码tips:
a.sum(axis=0)代表在垂直方向上求和,“=0”时会在水平方向上求和
reshape可以确保矩阵的尺寸
创建矩阵时避免创建(5,)而使用(5,1)来代替,否则输出的就不是一个矩阵而是数组
可以使用assert断言来确保创建的格式符合矩阵,或者用reshape来改变数据结构
在运算过程中还可能用到一个概论知识,最大似然估计,即通过结果求参数的过程。






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








