矩阵乘法与行列变换的理解小技巧

最新推荐文章于 2025-03-11 22:35:27 发布

zzxwchris123

最新推荐文章于 2025-03-11 22:35:27 发布

阅读量1.4k

点赞数 9

文章标签：矩阵算法人工智能

本文链接：https://blog.youkuaiyun.com/zzxwchris123/article/details/145657898

版权

之前在学校大一上线代课时，一直就是听老师说左乘矩阵行变换、右乘矩阵列变换的顺口溜，但始终没有用一种很形象化的方式去记忆，但今天突然灵机一动，发现可以这么来思考：

这是咱们的矩阵乘法用例：

A矩阵为：

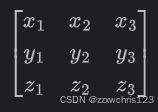
B矩阵为：

矩阵乘法为 A*B

左乘矩阵行变换：相当于A对B做行变换

左边的每一行的向量的每个值作为权重，去乘右边矩阵的每一个行向量后求加权和，然后作为左边矩阵的第一行。第二行第三行以此类推...

比如第一行就是

$x_1*[1,2,3]+x_2*[2,5,8]+x_3*[3,6,9]=$

$[x_1+4x_2+7x_3, 2x_1+5x_2+8x_3, 3x_1+6x_2+9x_3]$

右乘矩阵列变换：相当于B对A做列变换

右边的每一列的向量的每个值作为权重，去左边矩阵的每一个列向量后求加权和，然后作为右边矩阵的第一列。第二列第三列以此类推...

比如第一列就是

$1*[x_1,y_1,z_1]^T + 4*[x_2,y_2,z_2]^T + 7 * [x_3,y_3,z_3]^T =$

$[x_1+4x_2+7x_3, y_1+4y_2+7y_3, z_1+4z_2+7z_3]^T$

OK!希望能对大家有所帮助！还望大佬批评指正hhhhhhh

PS:

附上简陋的Latex代码

$$\left[ \begin{matrix}
   x_1+4x_2+7x_3 & 2x_1+5x_2+8x_3 & 3x_1+6x_2+9x_3\\
   y_1+4y_2+7y_3 & 2y_1+5y_2+8y_3 & 3y_1+6y_2+9y_3\\
   z_1+4z_2+7z_3 & 2z_1+5z_2+8z_3 & 3z_1+6z_2+9z_3
  \end{matrix}
  \right] = \left[
 \begin{matrix}
   x_1 & x_2 & x_3\\
   y_1 & y_2 & y_3\\
   z_1 & z_2 & z_3
  \end{matrix}
  \right] \left[
 \begin{matrix}
   1 & 2 & 3\\
   4 & 5 & 6\\
   7 & 8 & 9
  \end{matrix}
  \right] \tag{1}$$