Machine Learning Wu Enda2

chapter 6 Model representation

liner regression. this chapter see what the model looks like and what the overall process of supervised learning looks likes.

supervised learning ,has a data set ,called training set.

m =Number of traning examples
x’s = “input” variable/features
y’s =”output” variable/”target” variable
(x,y) - a single training example
(xⁱ,yⁱ) - ith training example

h - hypothesis
Housing price prediction model called linear regression, linear regression with one variable(univariate linear regression )

chapter 7 Cost function

-Housing price prediction
hypothesis:$h_{\theta} = \theta_0+\theta_1x$
$\theta_i$’s:Parameter
choose $\theta_0$,$\theta_1$ so that $h_{\theta}(x)$ is close to y for our training examples (x,y)

$$J(\theta_0,\theta_1)=\sum_{i=1}^{m}(h_\theta(x^i)-y^i)^2$$
Goal: $minmize_{(\theta_0,\theta_1)}J(\theta_0,\theta_1)$,
$J(\theta_0,\theta_1)$is Cost function or Squate error cost function

chapter 8 Cost function intuition 1

give some example to get back to intuition about what the cost function is doing and why we use it .

look up some plots to understand the cost function ,to do so ,we simplify the algorithm,so that it only had one parameter theta one.

chapter 10 Gradient descent

it is taking about gradient descent for minimizing some arbitrary function J.

Have some function $J(\theta_0,\theta_1)$
Want $min_{\theta_0,\theta_1} J(\theta_0,\theta_1)$
Outline:

• start with some $\theta_0,\theta_1$.
• keep changing $\theta_0,\theta_1$ to reduce $J(\theta_0,\theta_1)$ until we hopefully end up to a minimum.

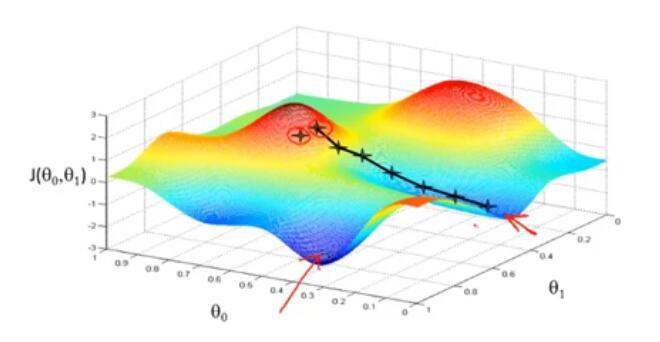
Gradient descent algorithm:

repeat until convergence {

$\theta_j := \theta_j-a\frac{\partial}{\partial \theta_j}J(\theta_0,\theta_1)$ (for j=0 and j=1)

}

a- called the learning rate,it basically controls how big a step we take downhill with gradient descent.

$\frac{\partial}{\partial \theta_j}$ - it is a derivative term

simultaneously update :

$temp0 :=\theta_0-a\frac{\partial}{\partial \theta_0}J(\theta_0,\theta_1)$

$temp1 :=\theta_1-a\frac{\partial}{\partial \theta_1}J(\theta_0,\theta_1)$

$\theta_0 := temp0$

$\theta_1 := temp1$

in the next chapter ,we’re going to go into the details of the derivative term.which it wrote out but didn’t really define.

chapter 11 Gradient descent intuition

get better intuition about what the algorithm is doing ,and why the steps of the gradient descent algorithm might make sense.

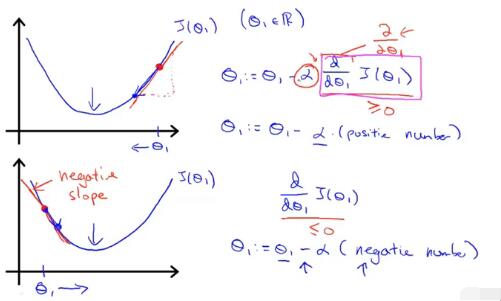
if $a$ is too small,gradient descent can be slow.

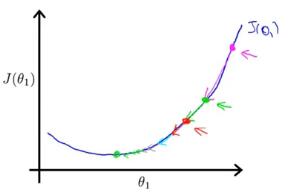
if $a$ is too large,gradient descent can overshoot the minimum.it may fail to converge or even diverge.

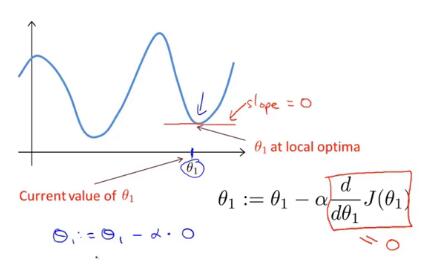
if you’re already at a local optimum,one step of gradient descent does absolutely nothing.It doesn’t change parameter.cause it keeps your solution at the local optimum.

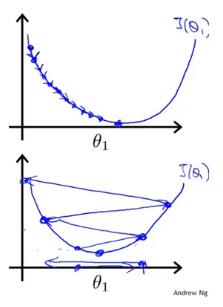
Gradient descent can converge to a local minimum,even with the learning rate $a$ fixed.

$\theta_j := \theta_j-a\frac{\partial}{\partial \theta_j}J(\theta_0,\theta_1)$

As we approach a local minimum.gradient descent will automatically take smaller steps.So,no need to decrease $a$ over time.

derivative term and partial derivative

chapter 12 Gradient descent for linear regression

put together gradient descent with our cost function,and that will give us an algorithm for linear regression for fitting a straight line to our data.

Gradient descent algorithm :

the key term we need is this derivative term over here.

$\frac{\partial}{\partial \theta_j}J(\theta_0,\theta_1) =\frac{\partial}{\partial\theta_j}\frac{1}{2m}\sum_{i=1}^{m}(\theta_0+\theta_1x^{(i)}+y^{(i)})^2$

$j=0 : \frac{\partial}{\partial \theta_0}J(\theta_0,\theta_1) = \frac{1}{m}\sum_{i=1}^{m}(\theta_0+\theta_1x^{(i)}+y^{(i)})·(\theta_0+\theta_1x^{(i)}+y^{(i)})\prime=\frac{1}{m}\sum_{i=1}^{m}(\theta_0+\theta_1x^{(i)}+y^{(i)})$

$j=0 : \frac{\partial}{\partial \theta_1}J(\theta_0,\theta_1) = \frac{1}{m}\sum_{i=1}^{m}(\theta_0+\theta_1x^{(i)}+y^{(i)})·(\theta_0+\theta_1x^{(i)}+y^{(i)})\prime=\frac{1}{m}\sum_{i=1}^{m}(\theta_0+\theta_1x^{(i)}+y^{(i)})·x^{(i)}$

“Batch” Gradient Descent :

“Batch”: Each step of gradient descent uses all the training examples.