LC.746 使用最小花费爬楼梯

题目描述：

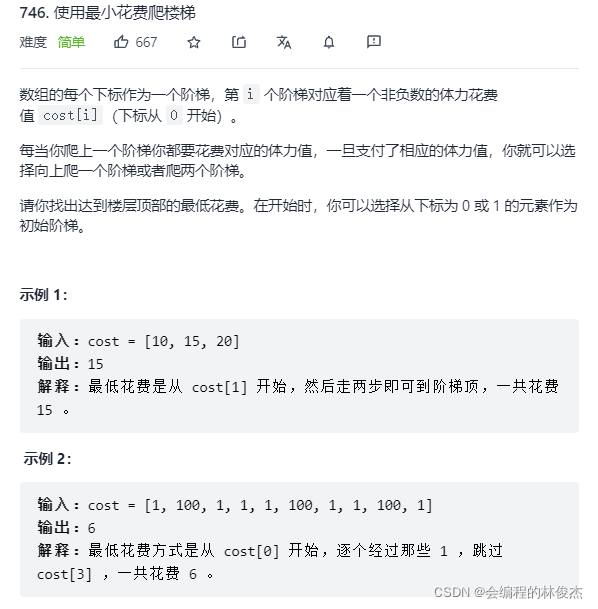
解法：

class Solution {

    public int minCostClimbingStairs(int[] cost) {

        int n = cost.length;

        int[] dp = new int[n];

        dp[0] = cost[0];

        dp[1] = cost[1];

        for(int i = 2; i < n; i++) {

            dp[i] = Math.min(dp[i - 1], dp[i - 2]) + cost[i];

        }

        return Math.min(dp[n - 2], dp[n - 1]);

    }

}

总结：

  在按照动规五部曲解题时，因为dp数组定义错误而导致无法正确解题。我将其错误定义为有i阶楼梯，dp[i]为爬上楼顶的最少花费体力，然后走了弯路，但其实可以发现，按照这个错误的定义是无法推出正确的结果的，如果发生这种情况就说明dp数组定义错误，我们需要重新定义。同时也说明了dp数组定义对解题的重要性。

  1）明确dp数组定义及下标含义：

    dp数组应正确定义为爬上第i阶楼梯花费的最少体力为dp[i]。

  2）推导递推公式：

    然后通过给定的第一个用例推dp[2]，一共有2层台阶（从0开始）。

    根据所要求的值，我们倒着看，因为从一个台阶可以选择向上爬一个或两个台阶，所以要达到楼顶有两个选择：

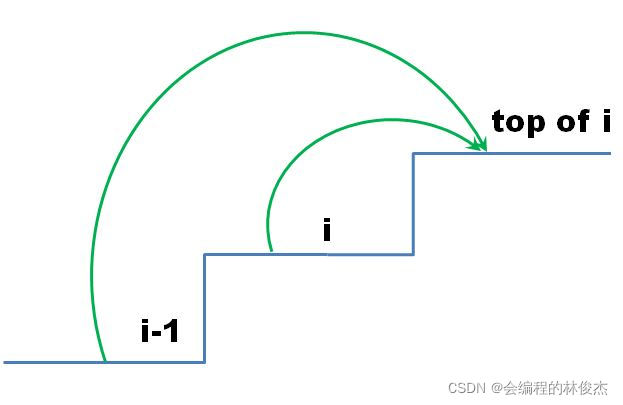
    选择1：从第i阶台阶再爬1阶台阶到顶，花费体力dp[i]；

    选择2：从第i-1阶台阶再爬2阶台阶到顶，花费体力dp[i-1]。

    所以到达第i级台阶的阶梯顶部的最小花费为minCost[i] = min(dp[i], dp[i-1])。

    那么接下来就是求爬上第i阶楼梯花费的最少体力 dp[i] 了。踏上第i级台阶有两种方法：

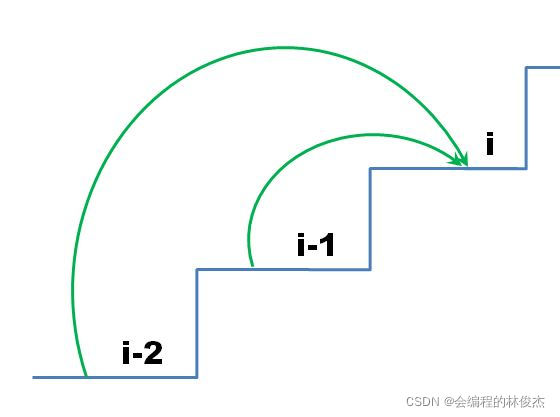
    方法一：先踏上第i-2级台阶（最小总花费dp[i-2]），再直接迈两步踏上第i级台阶（花费cost[i]），最小总花费dp[i-2] + cost[i]；

    方法二：先踏上第i-1级台阶（最小总花费dp[i-1]），再迈一步踏上第i级台阶（花费cost[i]），最小总花费dp[i-1] + cost[i]；

    则dp[i]是上面这两个最小总花费中的最小值。因此状态转移方程是：dp[i] = min(dp[i-2], dp[i-1]) + cost[i]。

  3）初始化：

    因为dp[i]是由dp[i- 1]、dp[i-2]推出，所以我们只需初始化dp[0]、dp[1]即可。又因为我们可以从第0阶或第一阶开始爬台阶，所以初始化为：

dp[0] = cost[0]、

dp[1] = cost[1]

  4）确定遍历顺序：

    依然因为dp[i]是由dp[i- 1]、dp[i-2]推出，所以从前向后遍历即可。

  5）若代码不通过可打印数组进行debug，这里就省略了。