知识干货（一）-机器学习（模型集成总结 一）

集成学习

在机器学习中的有监督学习算法中，研究的目标是学习出一个稳定的且在各个方面表现都比较好的模型，但实际情况往往不是那么的理想，有时候只能得到有偏好的模型（弱监督模型，在某些方面的表现比较好）。集成学习就是组合这里的多个弱监督模型以期得到一个更好更全面的强监督模型。可以说就是集百家之所长，能在机器学习算法中拥有较高的准确率。

•                      

 

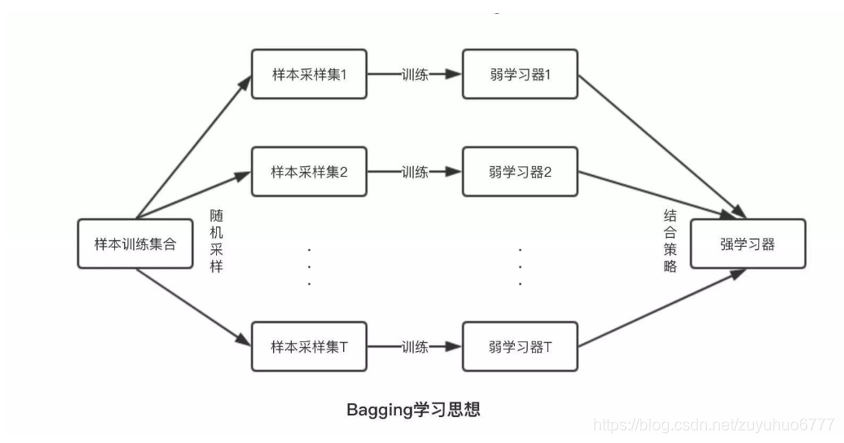
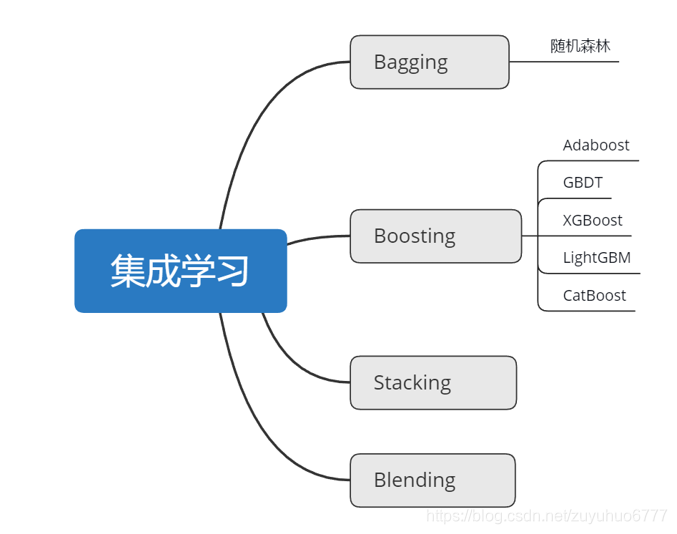
如图，目前常见的集成学习算法主要有以上四种：基于Bagging的算法和基于Boosting的算法，其中，基于Bagging的代表算法有随机森林等，基于Boosting的代表算法有     Adaboost、GBDT、XGBOOST等。

 

基于Bagging算法：

给定一个大小为n的训练集 D，Bagging算法从中均匀、有放回地选出 m个大小为 n'子集Di，作为新的训练集。在这 m个训练集上使用分类、回归等算法，则可得到 m个模型，再通过取平均值、取多数票等方法综合产生预测结果，即可得到Bagging的结果。

 

以随机森林为例:

随机森林由LeoBreiman（2001）提出，从原始训练样本集N中有放回地重复随机抽取k个样本生成新的训练样本集合，然后根据自助样本集生成k个分类树组成随机森林，新数据的分类结果按分类树投票多少形成的分数而定。

 

 

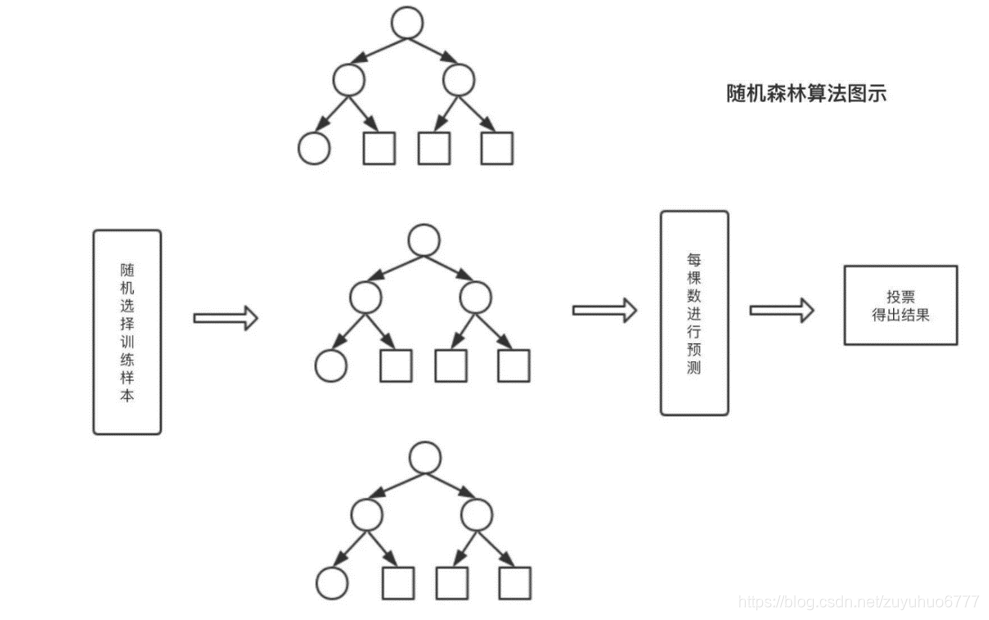
随机森林算法过程

1.从训练数据中选取n个数据作为训练数据输入，一般情况下n是远小于整体的训练数据N的，这样就会造成有一部分数据是无法被取到的，这部分数据称为袋外数据，可以使用袋外数据做误差估计。

2.选取了输入的训练数据的之后，需要构建决策树，具体方法是每一个分裂结点从整体的特征集M中选取m个特征构建，一般情况下m远小于M。

3.在构造每棵决策树的过程中，按照选取最小的基尼指数进行分裂节点的选取进行决策树的构建。决策树的其他结点都采取相同的分裂规则进行构建，直到该节点的所有训练样例都属于同一类或者达到树的最大深度。

4.重复第2步和第3步多次，每一次输入数据对应一颗决策树，这样就得到了随机森林，可以用来对预测数据进行决策。

5.输入的训练数据选择好了，多棵决策树也构建好了，对待预测数据进行预测，比如说输入一个待预测数据，然后多棵决策树同时进行决策，最后采用多数投票的方式进行类别的决策。

注意点：

1. 在构建决策树的过程中是不需要剪枝的。
2. 整个森林的树的数量和每棵树的特征需要人为进行设定。
3. 构建决策树的时候分裂节点的选择是依据最小基尼系数的。

实战：可以使用scikit-learn里面的包进行实战，具体信息可以参考【刘建平】老师的博客园：

1、https://www.cnblogs.com/pinard/p/6160412.html

 

 

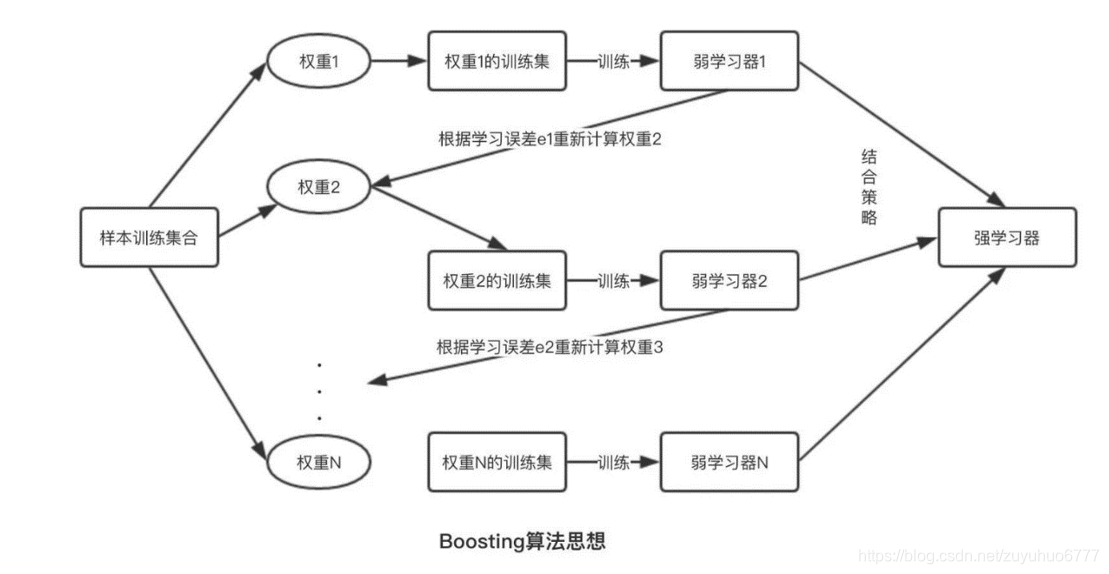
基于Boosting 算法

提升算法(Boosting)是常用的有效的统计学习算法，属于迭代算法，它通过不断地使用一个弱学习器弥补前一个弱学习器的“不足”的过程，来串行地构造一个较强的学习器，这个强学习器能够使目标函数值足够小。

 

基本思想

1.先赋予每个训练样本相同的概率；

2.然后进行T次迭代，每次迭代后，对分类错误的样本加大权重(重采样)，使得在下一次的迭代中更加关注这些样本。

 

Boosting系列算法里最著名算法主要有AdaBoost算法和提升树(boosting tree)系列算法。提升树系列算法里面应用最广泛的是梯度提升树(Gradient Boosting Tree)。

 

以AdaBoost算法作为代表算法详解

基本原理Adaboost(adaptive boosting: boosting + 单层决策树)是boosting中较为代表的算法，基本思想是通过训练数据的分布构造一个分类器，然后通过误差率求出这个若弱分类器的权重，通过更新训练数据的分布，迭代进行，直到达到迭代次数或者损失函数小于某一阈值。【牛顿法和梯度下降法】

                   

 

实战：

可以使用scikit-learn里面的包进行实战，具体信息可以参考【刘建平】老师的博客园：

1. https://www.cnblogs.com/pinard/p/6136914.html
2. https://www.cnblogs.com/pinard/p/6133937.html

 

基于Stacking 算法

将训练好的所有基模型对整个训练集进行预测，第j个基模型对第i个训练样本的预测值将作为新的训练集中第i个样本的第j个特征值，最后基于新的训练集进行训练。同理，预测的过程也要先经过所有基模型的预测形成新的测试集，最后再对测试集进行预测：

 

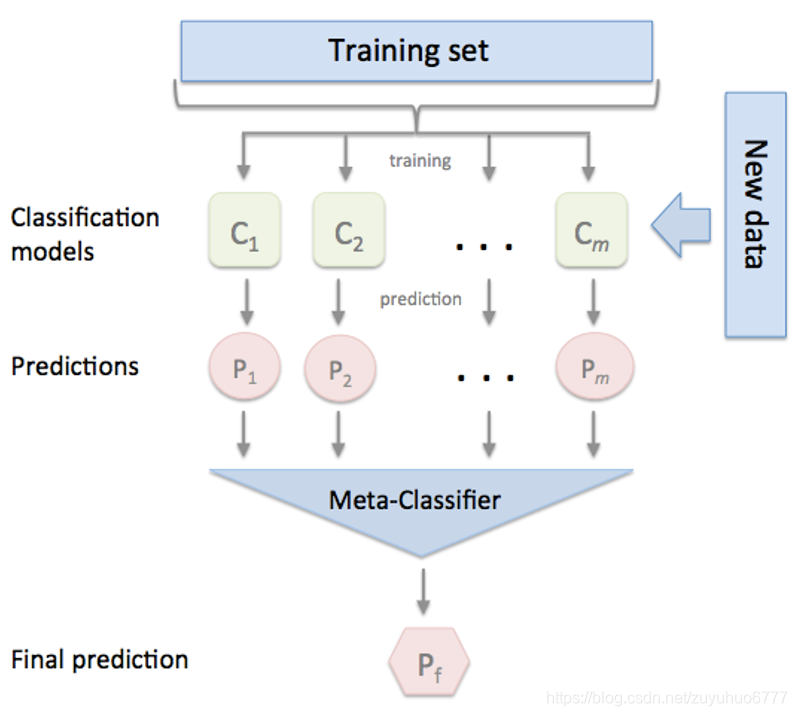
实践：推荐一款功能强大的stacking利器，mlxtend库，它可以很快地完成对sklearn模型进行stacking：

参考链接：

1. https://rasbt.github.io/mlxtend/user_guide/classifier/StackingClassifier/
2. https://blog.youkuaiyun.com/willduan1/article/details/73618677

 

 

集成学习之结合策略

本章对集成学习的结合策略做一个总结，我们假定有T个弱学习器 {h1,h2,…ht}.

 

 

 

链接：https://mp.weixin.qq.com/s/8o55k8zBoexvg7Gtc5G3Bw

更多精彩请关注公众号【AI算法与数学之美】

或者扫下方图片二维码奥

别忘记关注公众号与点  “在看”