Closest Common Ancestors
| Time Limit: 2000MS | Memory Limit: 10000K | |
| Total Submissions: 11754 | Accepted: 3875 |
Description
Write a program that takes as input a rooted tree and a list of pairs of vertices. For each pair (u,v) the program determines the closest common ancestor of u and v in the tree. The closest common ancestor of two nodes u and v is the node w that is an ancestor of both u and v and has the greatest depth in the tree. A node can be its own ancestor (for example in Figure 1 the ancestors of node 2 are 2 and 5)
Input
The data set, which is read from a the std input, starts with the tree description, in the form:
nr_of_vertices
vertex:(nr_of_successors) successor1 successor2 ... successorn
...
where vertices are represented as integers from 1 to n ( n <= 900 ). The tree description is followed by a list of pairs of vertices, in the form:
nr_of_pairs
(u v) (x y) ...
The input file contents several data sets (at least one).
Note that white-spaces (tabs, spaces and line breaks) can be used freely in the input.
nr_of_vertices
vertex:(nr_of_successors) successor1 successor2 ... successorn
...
where vertices are represented as integers from 1 to n ( n <= 900 ). The tree description is followed by a list of pairs of vertices, in the form:
nr_of_pairs
(u v) (x y) ...
The input file contents several data sets (at least one).
Note that white-spaces (tabs, spaces and line breaks) can be used freely in the input.
Output
For each common ancestor the program prints the ancestor and the number of pair for which it is an ancestor. The results are printed on the standard output on separate lines, in to the ascending order of the vertices, in the format: ancestor:times
For example, for the following tree:
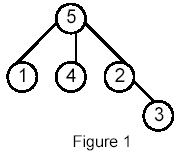
For example, for the following tree:

Sample Input
5
5:(3) 1 4 2
1:(0)
4:(0)
2:(1) 3
3:(0)
6
(1 5) (1 4) (4 2)
(2 3)
(1 3) (4 3)
Sample Output
2:1 5:5
Hint
Huge input, scanf is recommended.
Source
LCA的第一题就RE,数组扩大之后又MLE ,跪求大牛指点啊!!RE代码:
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;
#define N 50010
int n,m,q,e,eq;
int num[N];
int first[N],next[N],v[N],w[N];
int first_q[N],next_q[N],u_q[N],v_q[N],lca[N];
int d[N],p[N];
int flag[N];
bool ok[N];
void init()
{
e=eq=0;
memset(first,-1,sizeof(first));
memset(first_q,-1,sizeof(first_q));
memset(lca,0,sizeof(lca));
memset(p,-1,sizeof(p));
memset(ok,0,sizeof(ok));
}
void add(int a,int b)
{
v[e]=b;
next[e]=first[a];
first[a]=e++;
}
void add_q(int a,int b)
{
u_q[eq]=a;
v_q[eq]=b;
next_q[eq]=first_q[a];
first_q[a]=eq++;
}
void make_set(int i)
{
p[i]=i;
}
int find_set(int i)
{
if(i^p[i]) p[i]=find_set(p[i]);
return p[i];
}
void union_set(int i,int j)
{
i=find_set(i),j=find_set(j);
p[j]=i;
}
void dfs(int a)
{
int i,b;
make_set(a);
for(i=first[a];i!=-1;i=next[i])
{
b=v[i];
if(p[b]==-1)
{
dfs(b);
p[b]=a;
}
}
for(i=first_q[a];i!=-1;i=next_q[i])
if(!ok[i])
{
b=v_q[i];
if(p[b]!=-1)lca[i]=find_set(b),ok[i]=true;
}
}
inline bool get(int &a)
{
char c;
while(((c=getchar())<'0'||c>'9')&&c!=EOF);
if(c==EOF)return 0;
for(a=0;c>='0'&&c<='9';c=getchar())a=a*10+c-'0';
return 1;
}
int main()
{
int a,b,c,m,i;
char s1,s2,s3;
while(get(n))
{
init();
memset(flag,-1,sizeof(flag));
memset(num,0,sizeof(num));
for(i=0;i<n;i++)
{
get(a);get(m);
while(m--)
{
get(b);
add(a,b);
flag[b]++;
}
}
get(q);
while(q--)
{
get(a);get(b);
add_q(a,b);
add_q(b,a);
}
for(i=1;i<=n;i++)
if(flag[i]==-1)
{
dfs(i);
}
for(int i=0;i<eq;i+=2)
{
a=u_q[i];
b=v_q[i];
c=lca[i];
if(!c) c=lca[i+1];
num[c]++;
}
for(i=1;i<=n;i++)
if(num[i])printf("%d:%d\n",i,num[i]/2);
}
return 0;
}








 本文介绍了一种解决最近公共祖先(LCA)问题的算法,并提供了一个具体的编程实现案例。通过对输入数据的处理和树结构的遍历,该算法能够找出一对节点在树中的最近公共祖先。
本文介绍了一种解决最近公共祖先(LCA)问题的算法,并提供了一个具体的编程实现案例。通过对输入数据的处理和树结构的遍历,该算法能够找出一对节点在树中的最近公共祖先。
















 596
596

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








