现代密码学期末总结

写在前面

所用教材：杨波的现代密码学第四版
由于老师后来给画了重点，本篇博客后半部分主要记录的是老师画的重点。个人复习使用，仅供参考
对于河南大学的学弟学妹们，如果你们任课老师是袁老师的话，他会给复习要点，跟着复习要点有针对性的复习就行。

1.引言

知识点

1.在本书中，c指密文，m指明文，E()表示加密函数，D()表示解密函数

2.仿射变换：加密和解密中a，b为秘钥 （属于单表变换）

c=E_a,b(m)=am+b(mod 26)

m=D_a,b(m)=a^-1(c-b)(mod 26)

注意a^-1*a≡1 mod 26

3.多表代换密码：其中A为n*n的矩阵，n等于几代表明文每几个分成一组。一般N为26。

C_i≡AM_i+B(mod N)，i=1,2,3…

M_i≡A^-1(C_i-B)(mod N)，i=1,2,3…

4.人为攻击分为

• 被动攻击 就是窃听，是对系统保密性的攻击
  • 获取信息的内容
  • 业务流分析 敌收无法获得消息但可能获得通信双方身份、次数…
• 主动攻击 对数据流的篡改或产生假数据流
  • 中断 如破坏硬件、系统是对系统可用性的攻击
  • 篡改 修改数据是对系统完整性的攻击
  • 伪造 如插入伪造消息或记录，是对系统真实性的攻击

被动攻击不改变消息而主动攻击改变消息内容

抵抗被动攻击：预防 抵抗主动攻击：检测修复

5.密码算法的安全性包括哪两类？？(暂时没找到)

6.密钥管理：密钥产生、分配、存储、销毁等问题

7.密码体质从原理上可分为两类

• 对称(单钥)密码体制 （可用于数据加密和消息认证）
  • 流密码 逐位加密
  • 分组密码 消息分组，逐组加密
• 非对称(双钥)密码体制 两密钥，一公开一私密

8.对密码系统的攻击按攻击者可获取的信息量可分为

• 唯密文攻击 仅知道一些密文
• 已知明文攻击 知道一些密文和相应的明文
• 选择明文攻击 密码分析者可以选择一些明文并得到相应的密文
• 选择密文攻击 密码分析者可以选择一些密文，并得到相应的明文

以上攻击都建立在已知算法的基础之上，且攻击强度依次增加

9.单向陷门函数就是有一个陷门的一类特殊单向函数。

若y=f(x)，已知x很容易计算y，但已知y很难计算x（单向性）。特别的是存在一个z使得知道了z那么就很容易由y计算出x，那么z则称为陷门（有陷门也称后门）

10.加密算法满足下列两点则认为是计算上安全的

• 破译密文的代价超过被加密信息的价值
• 破译密文所花的时间超过信息的有用期

11.攻击密码体制的常用方法

• 穷举攻击 （解决方法 : 增大密钥量）
• 统计分析攻击 （解决方法：使明文的统计特性与密文的统计特性不一样）
• 数学分析攻击 （解决方法：选用足够复杂的加密算法）

12.密钥体制组成部分（加密系统的五元组）：明文，密文，密钥，加密算法，解密算法。

13.一个好密钥体制至少应满足的两个条件：

• 已知明文和加密密钥计算密文容易，已知密文和解密密钥计算明文容易
• 在不知解密密钥的情况下，不可能由密文 c 推出明文

14.清楚信息安全专业学习密码学的原因 （非标准答案）（必考！）

答：信息在社会中的地位和作用越来越重要，则其安全愈发重要，而密码学是保障信息安全的核心技术。可以说没有密码学就没有信息安全。

习题

1.设由仿射变换对一个明文加密得到的密文为edsgickxhuklzveqzvkxwkzukvcuh，又已知明文的前两个字符是“if"，对该密文解密。

答：e=4 d=3 i=8 f=5 （26个字母下标从0开始）E_a,b(m)=am+b(mod 26)

E(i)=e，4≡8*a+b(mod 26)

E(f)=d，3≡5*a+b(mod 26)

由上述两个式子可推出a=9，b=10，所以m=9^-1(c-10)(mod 26)

2.设多表代换密码C≡AM_i+ B(mod26)中，A是2X2矩阵，B是0矩阵，又知明文“dont”被加密为“elni”，求矩阵A。

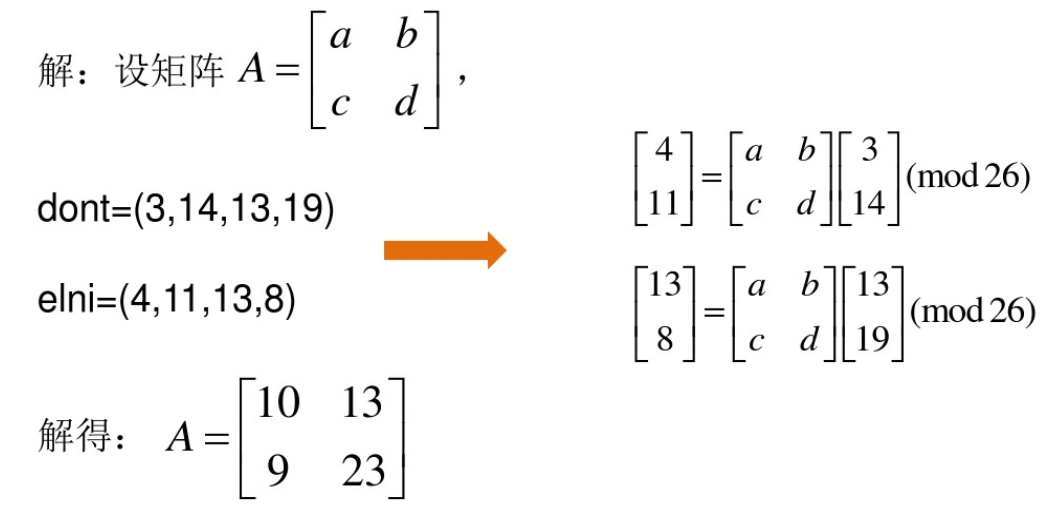
注意矩阵相乘的结果要模26，上式求b的时候算得125b=13，其实应是125b≡13(mod 26)，即为21b≡13(mod 26)，解得b=13，其他类似

2.流密码

知识点

1.流密码的基本思想： (必考！)

2.流密码中密钥流就等于明文串和密文串异或

3.移位寄存器是流密码产生密钥流的一个重要组成部分

4.m序列密码的破译就是求密钥流的递推关系即a_m+i=c_mai⊕c_m-1a_i+1⊕…⊕c₁a_m+i-1

(公式中的m即题目说多少级级线性反馈移位寄存器就是多少)

比如是3级，我们求得是a_i+3，当i=1，i+3=4即第四个这样根据前三个就可知道后面所有的数

习题

1.求矩阵的逆（这章习题会用到，复习下）

核心公式：A^-1=A^*/|A|

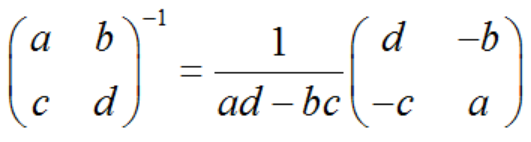
若是三阶矩阵：A_ij=(-1)^i+jM_ij，M_ij为除去a_ij所在那一行和那一列得到的二阶矩阵

2.已知流密码的密文串1010110110和相应的明文串0100010001，而且还已知密钥流是使用3级线性反馈移位寄存器产生的，试破译该密码系统。(和P65例2-6类似)

答：由已知可得密钥流为1010110110⊕0100010001=1110100111，因为是3级线性反馈

按照上面矩阵：a₄=c₃*a₁+c₂*a₂+c₁*a₃正是密钥流递推关系(m=3,i=1然后是m=3,i=2…)

记住c从高到低，a从低到高

3.如图是一个3级反馈移位寄存器，其初始状态为(a1,a2,a3)=(1,0,1)，求输出序列

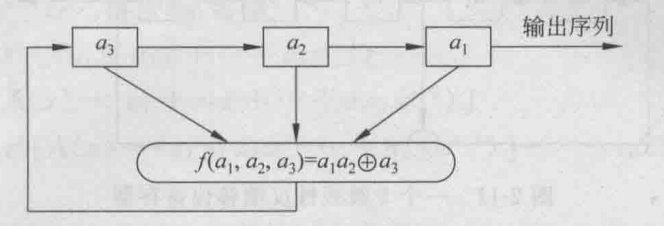
从图中可看到a1、a2、a3经f函数送至左边形成一个循环，比如f(a1,a2,a3)=b，那么b将代替a3的位置，a3～a1均右移，所以a1输出，以此类推。

答：f(a1,a2,a3)=f(1,0,1)=1*0⊕1=1，然后f(1,1,0)

可总结规律，右边的3为参与f函数生成的数放在左边，然后以左边这个数向右数3个数分别当做a3,a2,a1参与f生成的又放在最左边…最后输出是从右到左

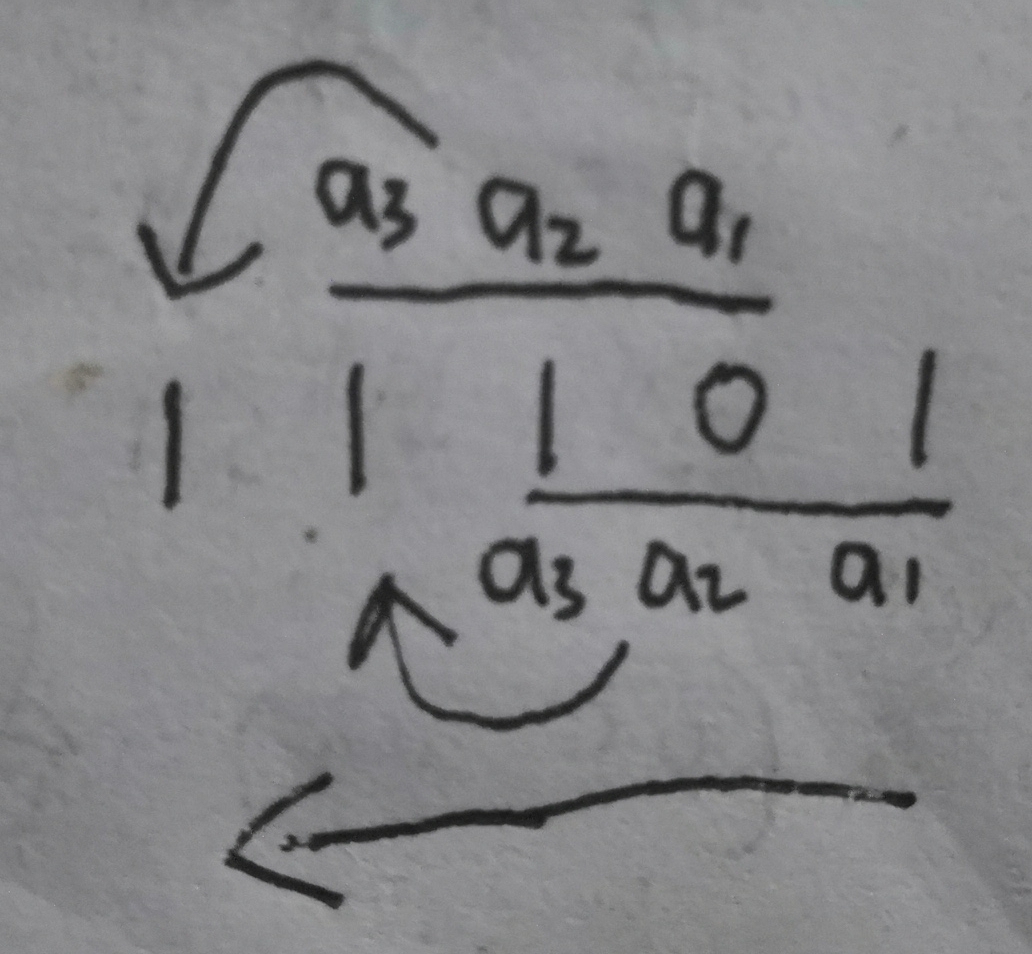
即输出序列为10111011101…，周期为4

3.分组密码

知识点

1.分组密码：将明文划分为长为n的组x(x0,x1,…,xn-1)，各组在密钥k=(k0,k1,…kt-1)控制下变换成等长的数字序列y=(y0,y1,…ym-1)。实质是对字长为n的数字序列的代换密码 （一般m=n）

2.扩散和混淆是Shannon提出的设计密码系统的两个基本方法(分组密码安全设计性原则) (了解)

• 扩散：使明文与密文之间的统计关系变得尽可能复杂，以使敌手无法得到密钥
  • 明文每一比特变换尽量多的影响密文序列的变化，以隐蔽明文的统计特性（雪崩效应）
  • P盒(置换)用于扩散
• 混淆：使密文与密钥之间的统计关系变得尽可能复杂，以使敌手无法得到密钥
  • S盒(代换)用于混淆

3.很多分组密码结构本质都基于Feistel结构

将每组明文分为左右两半L₀和R₀，n轮迭代后再合在一起产生密文分组

第i轮迭代（代换）： L_i=R_i-1 (左等右上) R_i=L_i-1⊕F(R_i-1,K_i) （右等左上异或F即右上和K）

最后一轮交换左右两半数据（置换）

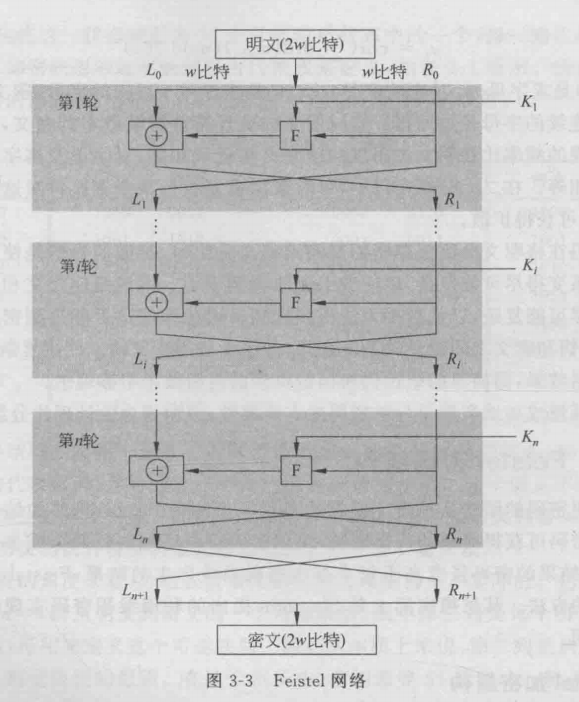
解密和加密本质过程一样，密文作为输入，但使用子密钥K_i的次序和加密相反（这一特性保证了加密和解密可用同一算法）

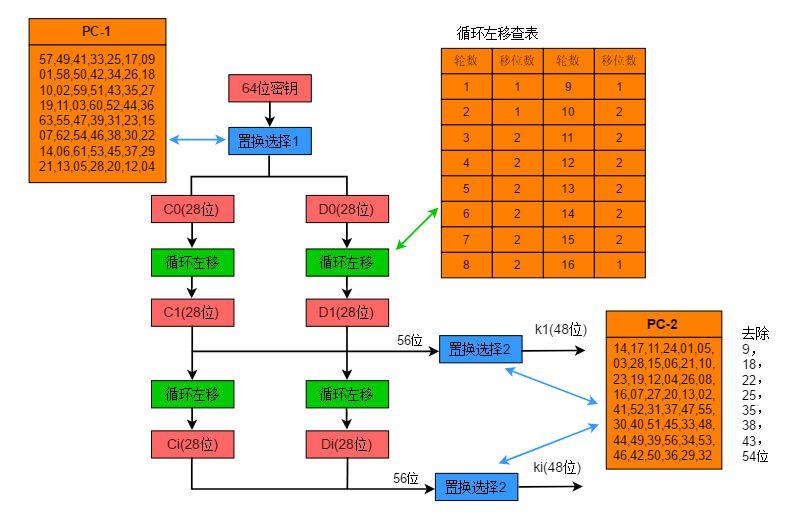
4.DES加密过程可分为三个阶段 (64比特明文，64比特密钥(每个第8位设置奇偶校验位实际56位)）

• 初始置换IP，用于重排明文分组的64比特 （由IP置换表实现）
• 生成子密钥
• 迭代过程即16轮变换(代换和置换)然后交换左右次序
• 逆初始置换IP^-1

2️⃣ 生成子密钥过程 参考：算法科普：神秘的 DES 加密算法 ，下同

56比特密钥经PC-1置换后分为左右C₀和D₀，然后由表左循环经PC-2产生48比特的本轮密钥

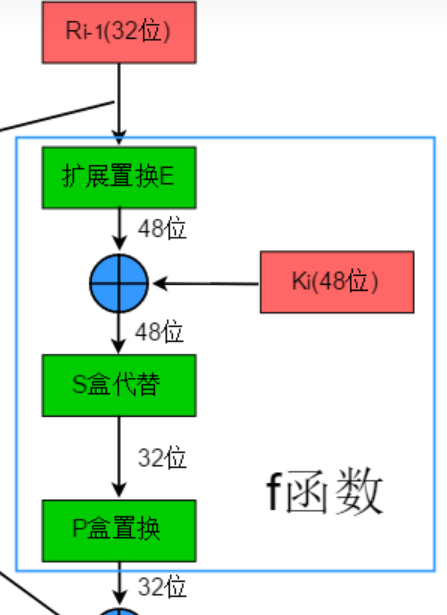
3️⃣ 迭代过程等同于Feistel结构(左等右上，右等左上异或F)，而其中用到的F函数为：

5.分组密码的运行模式

• ECB(电话本)模式 各明文组以同一密钥加密
• CBC(密码分组链接)模式 加密的输入是当前明文组和前一密文组的异或
• CFB(密码反馈)模式 每次处理j位输入，上次密文加密产生伪随机再与当前明文异或
• OFB(输出反馈)模式 与CFB不同的是加密的输入是前一次加密的输出(与明文异或的那个)

2️⃣ CBC模式加解密示意图 （必考！）

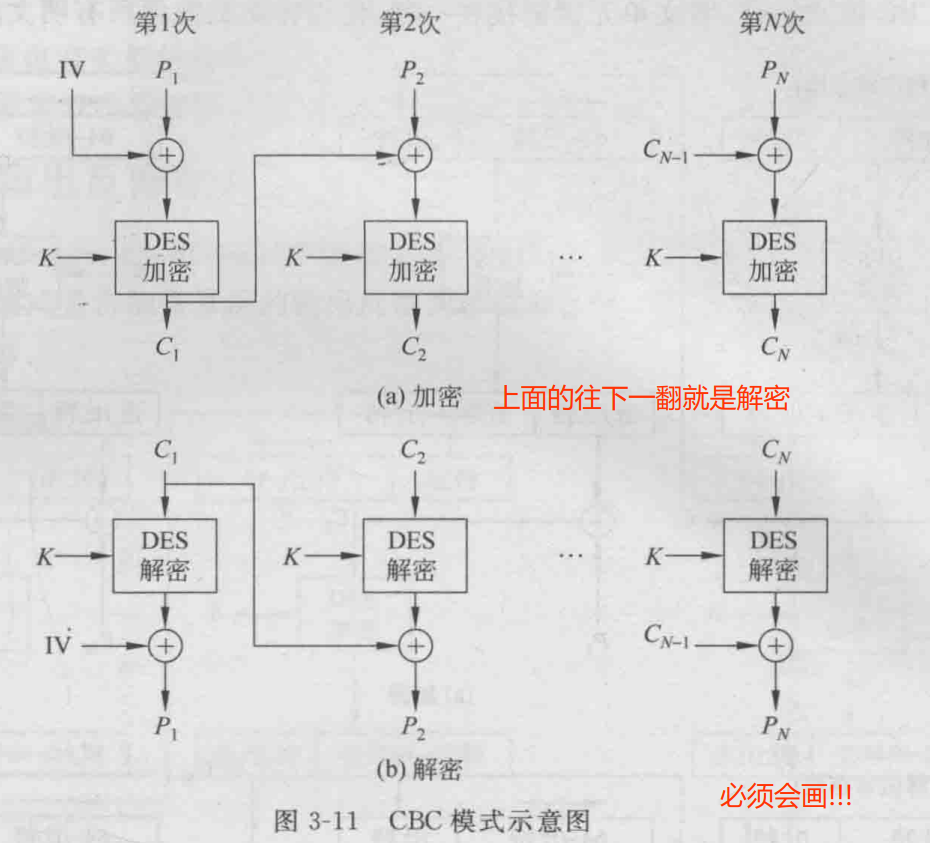
加密: C_i= E_k[P_i⊕C_i-1] (可认为C₀=IV) 解密:P_i= D_K[C_i]⊕C_i-1

IV初始向量与第一个明文分组异或，应像密钥一样被保护。该模式能够获得保密性也可认证，适合加密64比特的消息

工作模式为：它一次对一个明文分组加密，每次加密使用同一密钥，加密算法的输入是当前明文分组和前一次密文分组的异或，因此加密算法的输入不会显示出这次的明文分组之间的固定关系，所以重复的明文分组不会在密文中暴露出这种重复关系 （必须背会！）

6.AES是DES的替代者，也是当今最流行的对称加密算法之一

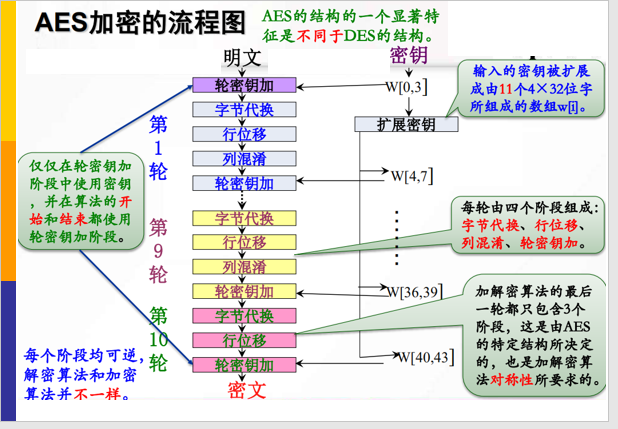
AES轮函数包括字节代换、行移位、列混合、密钥加

1️⃣ 字节代换：根据S盒把明文块的每一个字节都替代成另外一个字节

2️⃣ 行移位：如第1行不变，第2行循环左移C1个字节，第3行左移C2个字节，第4行移C3 要根据表

3️⃣ 列混合：输入数组每一列和修补矩阵的二维常量数组做矩阵相乘，得到对应的输出列。

4️⃣ 密钥加：输入数组的每个字节a[i,j]与密钥对应位置的字节k[i,j]异或一次，就生成了输出值b[i,j]

7.SM4算法，数据和密码分组均为128比特

加密：Xi+4=F(X_i,X_i+1,X_i+2,X_i+3,rk_i)=X_i⊕T(X_i+1⊕X_i+2⊕X_i+3⊕rk_i)（i=0,1,2…31）

后经反序R处理：(Y₀,Y₁,Y₂,Y₃)=(X₃₅,X₃₄,X₃₃,X₃₂)=R(X₃₂,X₃₃,X₃₄,X₃₅)

解密算法和加密算法相同，轮密钥使用顺序相反

8.GF(2⁸)中 a*a^-1=1(mod x8+x4+x5+x+1)

GF(2)上的可逆的仿射变换 （x是题目中a的逆）

习题

1.对字节a=1011 0110字节替代变换，设a的逆为a^-1 （ 必考！）

答：先求a的逆，再用仿射变换即可

1️⃣ 由a得(x⁷+x⁵+x⁴+x²+x)a^-1 ≡ 1(mod x⁸+x⁴+x³+x+1)

所以a^-1=x⁶+x⁵+x⁴+x³ 即0111 1000 （二进制对应位数有1就代表有x的那一次方）

根据老师给的考试要点，仿射变换和m(x)题目会给出，a的逆试试就出来了

2️⃣ 使用仿射变换 （注意要用a的逆而且注意x的顺序从下往上读）

即(0100 1110)₂=(4E)₁₆ 注意也是从下开始读 因为最下面的是字节高位即最前面的01…

2.利用DES算法和全0密钥对输入(1000 0001 1960 0000)进行一圈加密的结果 （需要查表P39）

答：1️⃣ 输入的右半部分是1960 0000 = 0001 1001 0110 0000 0000 0000 0000 0000

2️⃣ 经E盒扩展后为：000011 110010 101100 000000 000000 000000 000000 000000

3️⃣ 与全0密钥对异或后为：000011 110010 101100 000000 000000 000000 000000 000000

4️⃣ 经S盒后变为：15 8 3 7 2 12 4 13 即1111 1000 0011 0111 0010 1100 0100 1101

5️⃣ 经P盒后变为 1001 1100 1101 1000 1001 1010 1010 1110

6️⃣ 输出的左半部分即输入的右半部分为1960 0000，输出的右半部分为F函数输出和左半部分输入异或即8cd8 9aaf，最终输出为 1960 0000 8cd8 9aaf

这题主要是加深对DES迭代过程的理解，由于要查表，考试应该不会考

3.在DES的ECB模式中,如果在密文分组中有一个错误,解密后仅相应的明文分组受到影响。然而在CBC模式中，将有错误传播。加密解密图中C1中的一个错误明显地将影响到P1和P2的结果。

(1) P2后的分组是否受到影响?
(2)设加密前的明文分组P1中有1比特的错误，问这一错误将在多少个密文分组中传播?
对接收者产生什么影响?

答：1️⃣ CBC的加密: C_i= E_k[P_i⊕C_i-1]，i≥2 解密:P_i= D_K[C_i]⊕C_i-1，i≥1

若C1有错误，P2=D_K[C₂]⊕C₁所以P2也会受影响，但i≥3时，P_i= D_K[C_i]⊕C_i-1与C1无关因此不会受到影响

本题由于C1错误事实上C2、C3、C4…都会和原来不一样，但即使它是错的经密钥解密后还是可以得到原明文(可理解为是明文的另一种加密结果)，所以说P2后不受影响

2️⃣ 若P1出错，则C1会是错的，由C_i= E_k[P_i⊕C_i-1]得，C_i≥2也都是错误的，因此会传递到每一个分组

由加密解密方式可知，若只是P1出错，解密后得到的还是原来的输入。即接收者解密后的P1和原来输入的一样会有1比特的错误，而其他的可以解密得到正确的明文

4.公钥密码

知识点

1.RSA加密解密 (必考！)

选倆素数p,q n=p*q φ(n)=(p-1)*(q-1) d*e ≡ 1 mod φ(n)

加密：c ≡ m^e mod n （e和n会给出）

解密：m ≡ c^d mod n (一般d要自己求)

2.可能会用到的公式：a*b (mod q) = a (mod q) * b (mod q)

推测是RSA中m^e或c^d可以拆成两个乘积的形式

习题

1.RSA加密体制中，接收方的公开钥是(e,n)=(5,35)，接收到的密文是C=10，求明文M （必考！）

答：（ m ≡ c^d mod n 所以得先算出d -----> d*e ≡ 1 mod φ(n) ）

n=35 所以 p=5，q=7

φ(35) = (p-1)*(q-1) =4*6=24

因为 d*e ≡ 1 mod φ(n) 所以d=5 （这个到时候一个一个试就行）

m ≡ c^d mod n ≡ 10⁵ mod 35 ≡ 5 （注意不是等号）

2.假设明文m=5，e=7，p=11，q=13，给出RSA的加密解密过程 （必考！）

答：n=p*q=11*13=143 φ(143) = (p-1)*(q-1) = 10*12=120

因为d*e ≡ 1 mod φ(n) 即d*7 ≡ 1 mod 120 所以 d=103

加密：c ≡ m^e mod n ≡ 5⁷ ≡ 47 mod 143

解密：m ≡ c^d mod n ≡ 47¹⁰³ ≡ 5 mod 143

5.数字签名

知识点

1.ElGamal签名体制： （必考！）

用户A的公钥：y ≡ g^x (mod p) x为用户A的私钥

签名的产生过程：

• 计算 r ≡ g^k (mod p)
• 计算 s ≡ (H(m)-xr)k^-1 (mod p-1) H(m)为m的哈希值，计算取H(m)=m，注意是p-1
• (r,s)即为签名

签名的验证过程

• 计算y^rr^s ≡ g^H(m) (mod p)
• 就是验证 y^rr^s（mod p）是不是等于 g^H(m) (mod p)

习题

1.ElGamal签名体制中，假设p=19，g=13。签名者A的私钥为x = 10，试计算公钥。设消息M=15，k=11，求签名过程并验证。 (必考！)

答：公钥：y ≡ g^x mod p ≡ 13¹⁰ mod 19 = 6

签名：r ≡ g^k (mod p) ≡ 13¹¹ mod 19 =2

s ≡ (H(m)-xr)k^-1 (mod p-1) ≡ (m-xr)k^-1 (mod p-1) ≡ (15-10*2)*11^-1 mod 18 = 11

所以(r,s)=(2,11)

验证：y^rr^s ≡ 6²*2¹¹ mod 19 ≡ 8 ≡ g^m (mod p) ≡ 13¹⁵ ≡ 8 mod 19

根据老师的重点中给出的a*b (mod q) = a (mod q) * b (mod q)应该是用在比如这题求6²*2¹¹ mod 19就等同于求6² mod 19 * 2¹¹ mod 19 ≡ 17 *15 ≡ 8 mod 19

6.哈希函数

知识点

1.单向函数：已知h，求使得H(x)=h的x在计算上是不可行的。

2.弱单向哈希函数和强单向哈希函数 （必考！）

已知x，找出y (y≠x) 使得H(y)=H(x)在计算上是不可行的，若单向函数满足这种性质则称其为弱单向哈希函数 （必须会背！）

找出任意两个不同的输入x、y，使得H(x)=H(y)在计算上是不可行的，若单向函数满足这种性质则称其为强单向哈希函数 （必须会背！）

已知一个另找一个使得H函数相等是弱单向，任意给倆使其H函数相等是强单向（看谁单的很）

3.如果哈希函数对不同的输入可产生相同的输出，则称该函数具有碰撞性。

4.抗弱碰撞哈希函数：对于任意给定的x，找到满组足y≠x且H(x)=H(y)的y在计算上是不可行的

抗强碰撞哈希函数：找到任何满足H(x)=H(y)的x,y在计算上是不可行的

7.认证技术

知识点

1.消息认证是一个过程，用于验证接收消息的真实性(确实是它声称的实体发来的)和完整性(未被篡改、插入、删除)，同时还用于验证消息的顺序性和时间性(未重排、重放、延迟)以及消息的不可否认性。

8.密钥分配与密钥管理

知识点

1.Diffie-Hellman密钥交换简称D-H密钥交换的目的是使得两个用户能够安全的交换密钥，得到一个共享的会话密钥，算法本身不能用于加密解密。

2.D-H密钥交换协议： （必考！）

已知私钥为X，公钥为Y，p是一大素数，a是p的本原根，a和p公开，K为共享密钥

用户A：计算Y_A=a^XA mod p发送给B 共享密钥K=Y_B^XA mod p

用户B：计算Y_B=a^XB mod p发送给A 共享密钥K=Y_A^XB mod p

通过上述操作求得的两个K值相等，这样就安全的求得了一个公共的密钥

习题

1.在Diffie- Hellman密钥交换过程中，设大素数p=11,a=2是p的本原根。 （必考！）
(1) 用户A的公开钥Y_A=9,求其秘密钥XA。
(2)设用户B的公开钥Y_B=3,求A和B的共享密钥K。

答：1️⃣ Y_A=a^XA mod p = a^XA mod p 即 9=2^XA mod 11 所以 X_A=6 (考试时一个一个试就行)

2️⃣ K=Y_B^XA mod p = 3⁶ mod 11 =3

9.密码协议

知识点

1.密码协议是指利用密码工具实现与安全相关的协议或函数的计算

10.可证明安全

知识点

1.可证明安全性：将密码系统的安全性归结为某个经过深入研究的数学难题（如大整数素因子分解、计算离散对数等），数学难题被证明求解困难。这种评估方法存在的问题是它只说明了这个密码方法的安全性与某个困难问题相关，没有完全证明问题本身的安全性。

11.密码学新方向

知识点

1.写出5中密码学新方向或新技术 （必考！）

答：身份基加密(IBE)、属性基加密(ABE)、全同态加密、动态加密