差分进化算法DE（Differential Evolution）算法是在遗传算法等进化思想的基础上提出的

差分进化算法DE（Differential Evolution）算法是在遗传算法等进化思想的基础上提出的，本质是一种多目标（连续变量）优化算法，用于求解多维空间中整体最优解。
Matlab 程序

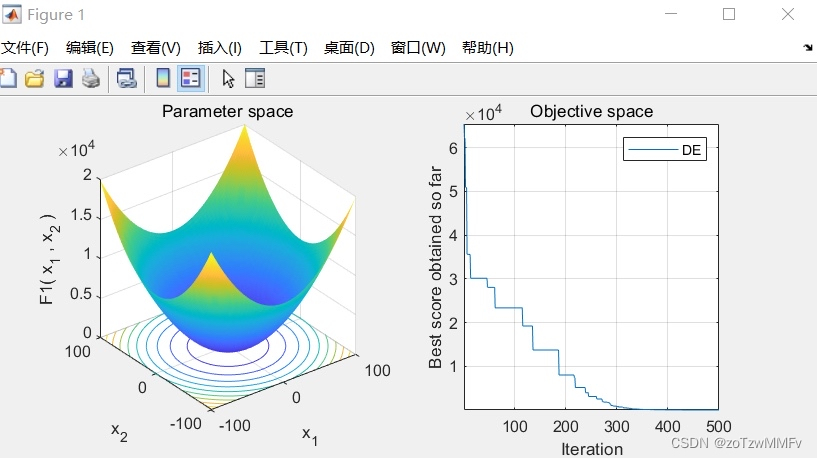
差分进化算法（Differential Evolution）是一种多目标优化算法，它基于遗传算法等进化思想的基础上进行了改进和创新。本文将介绍DE算法的原理和应用，并通过编写Matlab程序来实现该算法。

一、差分进化算法的原理 差分进化算法的本质是一种多目标优化算法，它主要用于求解多维空间中的整体最优解。在DE算法中，通过引入差分操作来更新种群中的个体，以实现种群的进化和优化。其具体步骤如下：

1. 初始化种群 首先，需要随机生成一组个体作为初始种群。这些个体代表了问题空间中的潜在解，并且通过编码方式进行表示。

2. 选择操作 在DE算法中，选择操作主要是通过比较个体之间的适应度来选择优秀的个体。常用的选择操作有锦标赛选择、轮盘赌选择等。

3. 变异操作 变异操作是DE算法的核心步骤之一。它通过引入差分变异来改变种群中个体的基因组合，以增加种群的多样性和全局搜索能力。

4. 交叉操作 交叉操作是为了产生新的个体，并保留原始个体的优良基因。它通常包括两个个体之间的基因交换或基因重组等操作。

5. 更新种群 根据变异和交叉操作后得到的新个体，更新整个种群。更新的方式可以是完全替换、部分替换或者保留部分优秀个体等。

6. 终止条件 DE算法的终止条件可以是达到最大迭代次数、种群适应度达到一定阈值或者经过一定时间等。

二、差分进化算法的应用 差分进化算法在实际应用中得到了广泛的应用和研究。它可以用于解决各种优化问题，如函数优化、参数优化、模型参数估计等。下面以函数优化为例，介绍DE算法的应用。

在函数优化问题中，我们需要找到一个函数在给定约束条件下的最优解。DE算法可以通过迭代优化的方式来逐步逼近最优解。具体的步骤如下：

1. 定义问题 首先，需要明确函数优化问题的目标，包括目标函数和约束条件。目标函数可以是单目标函数或多目标函数。

2. 设计适应度函数 适应度函数是用来评估每个个体的优劣程度。在函数优化问题中，适应度函数一般是目标函数的值。

3. 设置参数 DE算法中有一些重要的参数需要设置，如种群大小、变异因子、交叉概率等。这些参数的设置对算法的性能和效果有重要影响。

4. 编写算法程序 根据DE算法的原理和步骤，编写相应的算法程序。可以使用Matlab等编程语言来实现DE算法。

5. 迭代优化 通过迭代优化的方式，不断更新种群，直到满足终止条件。在每一次迭代中，根据变异和交叉操作，生成新的个体，并更新整个种群。

6. 输出结果 在DE算法运行结束后，输出最优解和相应的适应度值。可以进行可视化分析，比较优化前后的差异。

三、Matlab程序实现DE算法 下面是一个简单的Matlab程序实现DE算法的示例：

function [bestSolution, bestFitness] = DEAlgorithm(func, numVar, popSize, maxIter)

    % 初始化种群
    population = rand(popSize, numVar);

    for iter = 1:maxIter
        
        % 计算种群的适应度
        fitness = func(population);
        
        % 选择操作
        [sortedFit, idx] = sort(fitness);
        population = population(idx, :);
        
        % 变异操作
        mutant = population + 0.5 * (population(randi(popSize, popSize, 1), :) - population(randi(popSize, popSize, 1), :));
        
        % 交叉操作
        cross = rand(popSize, numVar) < 0.8;
        offspring = population;
        offspring(cross) = mutant(cross);
        
        % 更新种群
        population = offspring;
        
    end
    
    % 输出结果
    [bestFitness, idx] = min(fitness);
    bestSolution = population(idx, :);
    
end

在这个示例程序中，首先定义了一个DEAlgorithm函数，该函数接受目标函数、变量个数、种群大小和最大迭代次数作为输入。在函数体内部，按照DE算法的步骤依次进行种群初始化、选择操作、变异操作、交叉操作和种群更新。最后输出最优解和相应的适应度值。

四、总结 差分进化算法是一种多目标优化算法，可以用于求解多维空间中的整体最优解。本文介绍了DE算法的原理和应用，以及通过编写Matlab程序实现DE算法的方法。DE算法在函数优化等领域具有广泛的应用前景，希望本文的介绍对读者有所帮助。

相关代码,程序地址：http://lanzouw.top/673225474378.html