本文深入讲解了递归的概念，条件和作用，通过实例解析了递归实现strlen、阶乘、斐波那契数列及无符号整型顺序打印。讨论了递归的优缺点，并对比了循环解决斐波那契数列的方法。最后预告了递归在青蛙跳台阶和汉诺塔问题的应用。
晚上好哇！话不多说，直入主题。
函数的递归其实是一种算法问题，有一定难度，理解和使用需要较高的熟练度，在这里，只要先学会写一些常见的递归即可。
目录
1.什么是递归
我们知道函数在定义之后可以被调用，同时，函数也可以进行调用其他函数，即嵌套递归，那函数可以调用自己吗？答案当然是可以的，函数递归的本质正是函数自己对自己的重复调用。
1.1补充：栈帧
在讲具体的递归之前，我们来渗透一下程序地址空间的简单布局（目前可把程序地址空间当作内存理解，但实际上两者并不相等），
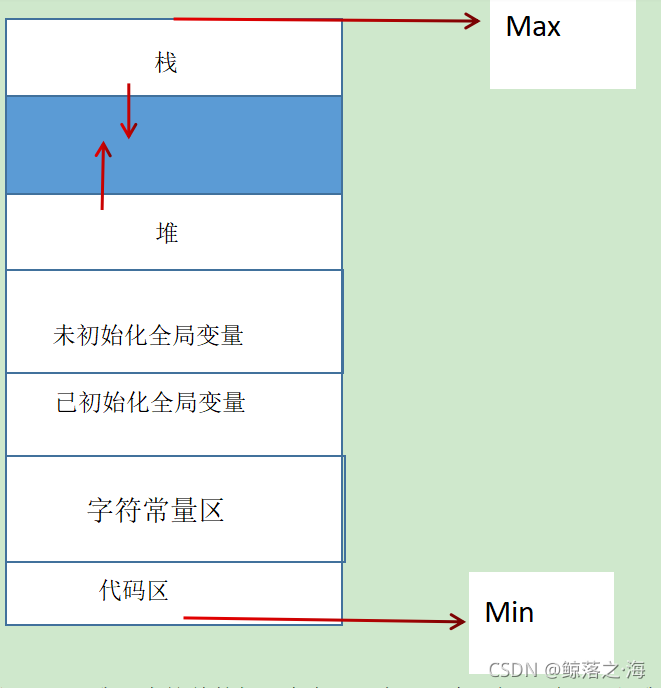
如该图所示，我们先简单的把“内存”分为这几个空间，最下面是我们的代码区域，然后向上依次‘字符常量区’‘已初始化全局变量’‘未初始化全局变量’‘堆’‘栈’,今天我们只讲栈区的部分知识。
在“内存”图中，地址由下至上依次增长，最上面是最高地址，最下面是最低地址，如上图示（min，max）。
在“内存”中，栈区和堆区相对而上，堆区依次向上存储数据，而栈区向下存储数据。
栈区内存储的是临时变量（局部变量）（自动变量），由于函数内部的变量都是临时变量，因此均存储在栈区，即当一个已经被定义的函数被调用时，该函数会在栈区开辟一块空间，这块空间叫作栈帧，而所有在该函数内定义的临时变量，均会存储在该函数的栈帧中，自上而下进行存储。
每个函数的开辟都是新的栈帧的开辟，因此每次调用函数都会形成栈帧，
这当然也包括main函数，至于main函数被谁调用（当然是被调用了）暂时不理会，main函数一被调用就会形成一个main的栈帧，若main函数中再次调用其他函数，如调用Add函数，则在main栈帧的下面就会再次开辟一个Add函数的栈帧，依次累推。
当该函数被调用完毕（执行完毕后）该栈帧就会被释放，即释放对应地址空间，栈帧中的临时变量也是如此，每次执行完该函数，该函数内部的临时变量空间被释放，也正是因此我们称之为临时变量，也因此有了作用域和生命周期。
但堆栈之间的空间并不是无限的，当函数调用过多时，就会形成过多的栈帧，而栈帧的开辟和释放都会消耗时间，因此我们认为函数的调用是有成本的，即时间和空间成本，时间成本即栈帧的开辟和释放，空间成本就是对栈下有限空间的占据。
2.递归的条件：
这是一个非常简单地递归，在进入Print函数后，不断地进行自我的重复调用。但很显然，该程序是违法的，因为每次Print的调用都会开辟栈帧，栈区是有限的，而递归是无限的，因此会出现栈溢出（即Stack Overflow）错误。
如盗梦空间中两面镜子相对，进入镜子套镜子的无限循环，导致梦境破碎，是因为大脑计算容量不够
计算机既然是为人服务的，就要满足实际生活中的情况，而在实际生活中，并不存在无限递归（难道存在有人做梦梦到梦中的自己在做梦，而做的梦还是梦中的自己在做梦这样的无限递归吗，因为大脑的有限，所以是不存在的）。
因此，每一个递归都必须有自己的出口（即自己的限制条件），即在完成某项事情后找到出口，停止递归。
由于递归要在不断调用中找到出口，因此要求每次递归都必须更加接近递归的限制条件，如此才能在某刻跳出递归，而不是距离条件越来越远或者不变。
3.递归的作用：
递归就是把一个较为复杂的问题进行连续拆分，将该问题的解决变成若干个子问题的解决，而这些子问题是有联系的，当拆分到足够小时，最后一个子问题就已经解决掉了（这就是出口），由此回推，每一个问题都可以得到解决，总结就是——大事化小，小事化了
4.小练习
4.1递归实现库函数strlen的功能：
#pragma warning(disable:4996)
#include<stdio.h>
int MyStrlen(char* parr)
{
if(*parr == '\0') {
return 0;
}
else{
return (1 + MyStrlen(parr + 1));
}
}
int main()
{//递归实现strlen
//首先要有一个字符串
char arr[] = "abcdef";
int ret = MyStrlen(arr);
printf("%d\n", ret);
return 0;
}
解析：
递归的条件是能够将问题分成子问题，且有递归出口。
我们要解决的问题是 求字符串arr（“abcdef”）的长度，该问题可分解为 1+字符串（“abcde”）的长度，而“abcde”的长度又可以分为 1+“abcd”的长度，依次递归下去，直到遇到“\0”时，递归停止。
分析：
初始化一个字符串，调用MyStrlen函数，在栈区开辟一个栈帧，所传形参为数组首元素的地址，以char类型的指针进行接收，则指针变量parr指向数组首元素地址，因此*parr就相当于数组的首元素，当*arr不为”\0”时，再次调用函数MyStrlen，向下继续开辟一个栈帧，所传形参为 1+parr ，parr是数组首元素的地址，则parr+1就是数组第二个元素的地址（指针为char类型，因此parr+1，每次加一个字节，当指针类型为int时，，每次向后读取4个字节，在指针篇会解释，暂时明白类型不同指针加减结果不同即可），*（arr+1）就是第二个元素，当第二个元素不是”\0”时，继续递归，知道数组的某一位恰好是”\0”时，此时递归停止，函数开始依次返回值，释放栈帧，最后返回即为该字符串的长度。
图解“abc\0”的调用和返回流程
4.2.递归实现n的阶乘
#pragma warning(disable:4996)
#include<stdio.h>
int Fact(int n)
{
if (n == 1)
{
return 1;
}
return n * Fact(n - 1);
}
int main()
{
int n;
scanf("%d", &n);
int ret = Fact(n);
printf("%d\n", ret);
return 0;
}
思路：
n！=n *（n-1）！当n=1时，递归结束，返回1
4.3递归计算裴波那契数列第n个数的值
#pragma warning(disable:4996)
#include<stdio.h>
int Ponachi(int n)
{
if (n <= 2)
{
return 1;
}
return Ponachi(n - 1) + Ponachi(n - 2);
}
int main()
{
//斐波那契数列 > 0 1 1 2 3 5 8 13.....
//我们这里从1开始计算裴波那契,即第一个数是1，第3个数是2
//求斐波那契数列第n个数的值
int n;
scanf("%d", &n);
int ret = Ponachi(n);
printf("%d\n", ret);
return 0;
}
思路：
当n>2时，第n个数的值为前两个数值之和：Ponachi（n）=Ponachi(n - 1) + Ponachi(n - 2);
当n=1或2时，返回1；
注意：
当n足够大的时候，阶乘和裴波那契数列都有溢出风险，我们这里并不考虑数据的溢出问题。
4.4无符号整型的顺序打印
//无符号正数的顺序打印
#pragma warning(disable:4996)
#include<stdio.h>
void MyPrint(int x)
{
if (x > 9)
{
MyPrint(x / 10);
}
printf("%d ", x % 10);
return;
}
int main()
{
unsigned int x;
scanf("%d", &x);
MyPrint(x);
return 0;
}
注意：
最后一个调用的MyPrint首先执行打印语句 ，因此打印是由最后一个MyPrint开始，随着栈帧的释放有后到前打印的，而最后一个MyPrint存的是第一位，因此为顺序打印。
5.递归的特性（优点和缺点）
5.1优点：代码简单，赏心悦目。
5.2缺点：
递归要多次调用函数（甚至进行多次重复计算），而函数的调用需要成本（栈帧的开辟和释放），导致递归效率较低。
如裴波那契数列的递归，如我们要算第5个数，那我们要先算第4个数和第3个数，而我们要算第4个数，要计算第3个和第2个数，此时就已经对第3个数进行了两次重复运算了，因此n越大，其重复计算次数就会越多（类似于一个树状图，呈扩散趋势，越往下重复运算越多），导致裴波那契数效率较低，可以把代码写出来输入10试试，在输入60甚至更大试试，发现延迟较大。
小图例：
递归其实也算是一种循环，因此当某些问题既可以用递归又可以用循环解决时，建议使用循环，除非循环过于繁琐。
5.3裴波那契数列的循环解决
#pragma warning(disable:4996)
#include<stdio.h>
//1 1 2 3 5 8 13 21
int Fib(int n)
{
int third;
int first = 1, second = 1;
while (n > 2)
{
n = n - 1;
third = first + second;
first = second;
second = third;
}
return third;
}
int main()
{
int n;
scanf("%d", &n);
int ret =Fib(n);
printf("%d\n", ret);
return 0;
}
下篇将使用递归解决两个实例：
青蛙跳台阶问题
汉诺塔递归问题
大家尽量先熟悉一下，因为递归基本思路已经讲过，我-将不会赘述一些基础。
晚安哇！（今天可是我生日哇——留个赞呗（可怜））
扫一扫
1268
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
