计算机算法设计与分析 | 网络流

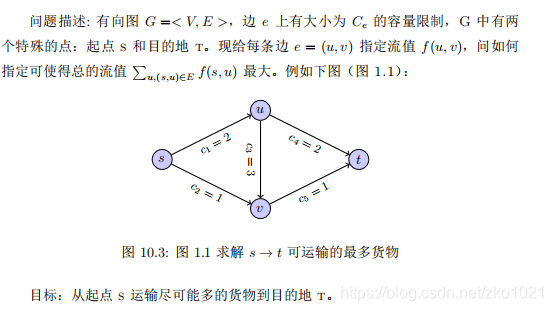
我们关注最大流问题，具体例子如下图：

 

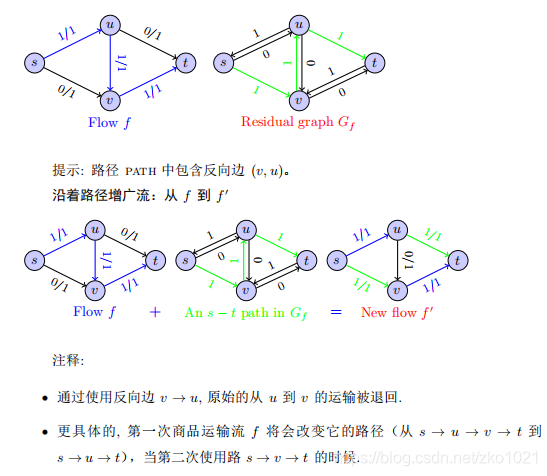
重要定义：剩余图

即，在剩余图中，u,v之间包含2条边：

反向边(v,u)，容量为f(e)；正向边(u,v)，容量为C(e)-f(e)。

 

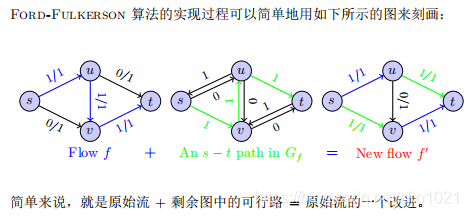
增加：可退回边

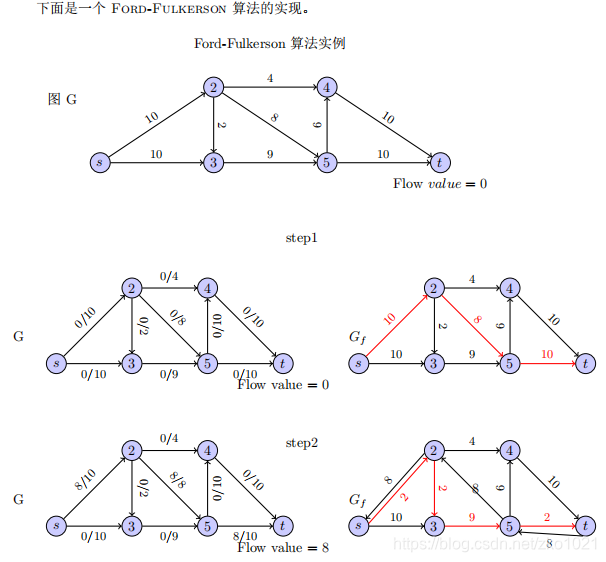
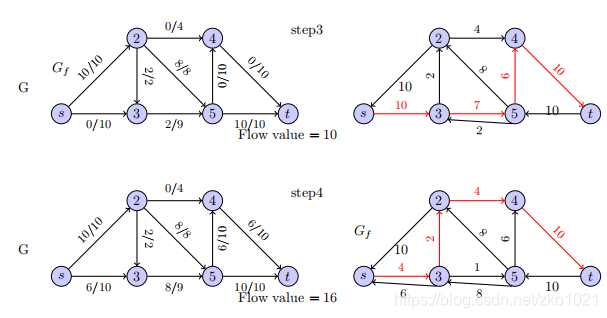
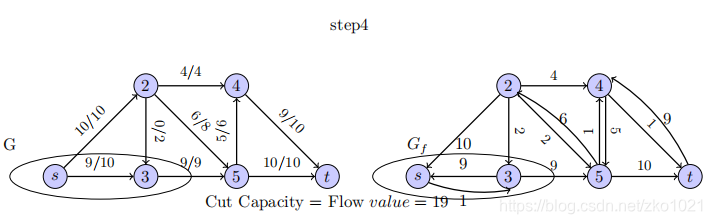
这里step3 的剩余图 5->4 应该是10，而不是6；

这样的话，step4的左图（即优化后的路径），s->3为7，后续依次类推。

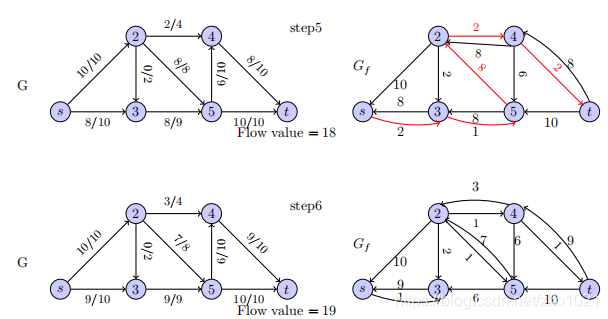
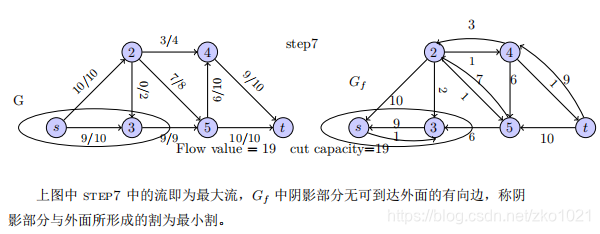
到最后一步，剩余图中再选不出s->t的路径的时候，就是算法停止的时候。

 

Dinic算法

顶点的层次：在剩余图中，把从源点到顶点u的最短路径长度，称为顶点u的层次。源点（下图中的Vs）的层次为0。

下图就是一个分层的过程。

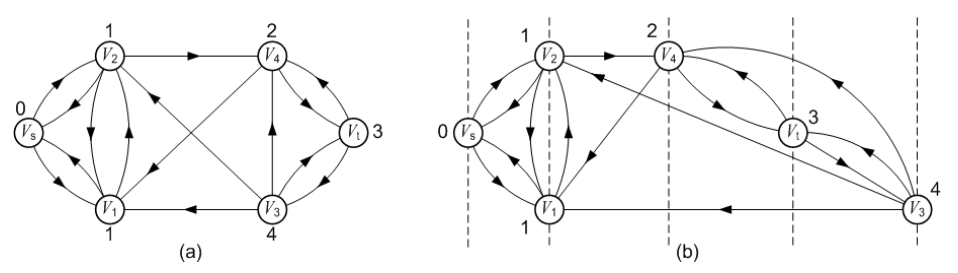
最短路增广路径的算法思想

每次在分层网络中找一条含弧数最少的增广路进行增广。

具体步骤如下：

（1）初始化容量网络和网络流。

（2）构造剩余图和分层网络，若汇点(t)不在分层网络中，则算法结束。

（3）在层次网络中不断用BFS增广，直到分层网络中没有增广路为止；每次增广完毕，在分层网络中要去掉因改进流量而导致饱和的弧。

（4）转步骤（2）。

Dinic其实是最短增广路算法的优化版。

 

对于Dinic算法，重点关注两个部分：

1. 阻塞流：用O(m)的时间构造分层网络GL，每得到一个GL，不断进行增广，直到没有路径。

2. 用DFS搜索增广路径。

 

算法实现

Initialize f(e) = 0 for all e.
while TRUE do
     Construct layered network GL from residual graph Gf ;
     if dist(s, t) = ∞ then
         break;
     end if
find a blocking flow f′ in GL using DF S technique;
     augment flow f by f′;
end while
return f;

阻塞流代表在 GL 网络中经过该流的增广，不再存在 s − t 的路径。

在使用 O(m) 时间得到一个分层网络后，EDMONDS-KAPR 每次只增广一条路径（效率较低）。

 

算法实例

 

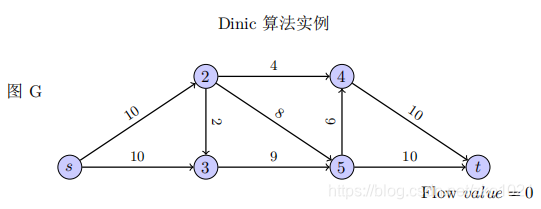
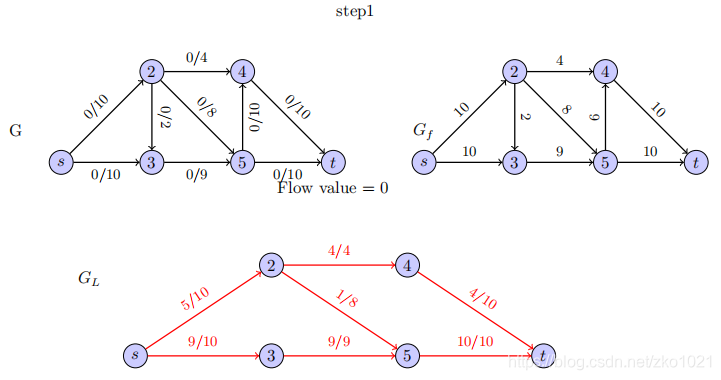
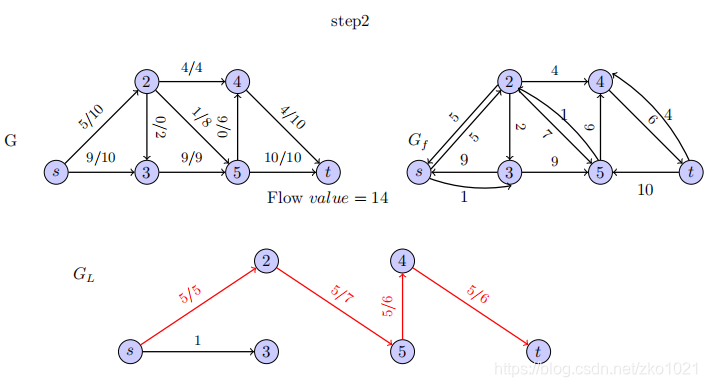
初始网络流；剩余图；

分层网络GL：去掉饱和边  ->  找到一条s-t的最短路径。

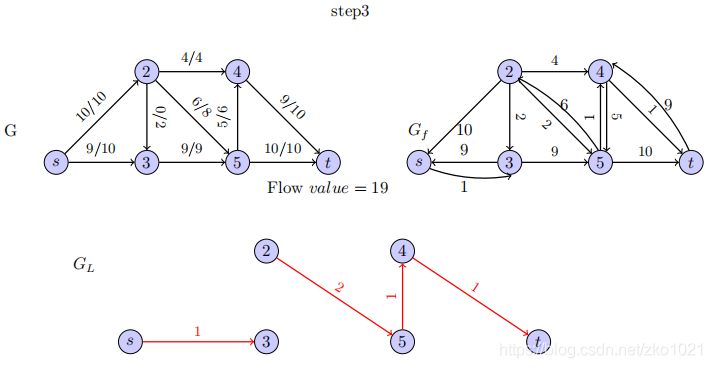
此时，找不到s-t的完整路径，算法停止。

 

 

算法分析

总的时间复杂度为 O(mn2)

• 构造分层网络：O(m)（扩展的 BFS）

• 寻找阻塞流：O(mn)。其中，

    1) 用 DFS 在分层网络中寻找一条 s − t 路径需要 O(n) 时间。

    2) 每条路径至少饱和一个 bottleneck 边。因此，寻找一条阻塞流至多需要 m 次迭代。

• #while = O(n)(与 EDMOND-KARP 增广过程分析相同)

    因此总的时间复杂度为 O(mn2)