【网络表示学习】node2vec

最新推荐文章于 2024-04-15 17:20:00 发布

zjwreal

最新推荐文章于 2024-04-15 17:20:00 发布

阅读量1.3k

点赞数 1

CC 4.0 BY-SA版权

分类专栏：网络表示学习网络表示学习文章标签：网络表示学习 Network Embedding

本文链接：https://blog.youkuaiyun.com/zjwreal/article/details/90551515

node2vec是KDD 2016上提出的一种图嵌入技术，它扩展了deepwalk，结合了DFS和BFS的随机游走策略。通过参数p和q控制游走模式，寻找节点的结构相似性和同质性之间的平衡。模型的目标是最大化节点及其近邻出现的概率，使用条件独立性和特征空间对称性假设简化优化问题，并采用负采样技术进行求解。此外，还介绍了有偏随机游走的策略和学习算法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目：node2vec: Scalable Feature Learning for Networks

作者：Aditya Grover and Jure Leskovec

来源：KDD 2016

源码：https://github.com/aditya-grover/node2vec

node2vec是一种综合考虑DFS邻域和BFS邻域的graph embedding方法。简单来说，可以看作是deepwalk的一种扩展，是结合了DFS和BFS随机游走的deepwalk。

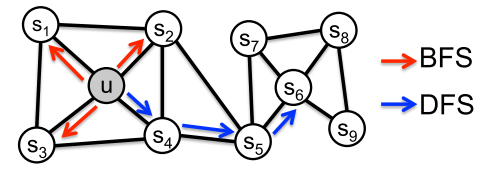
其中BFS对应结构相似性，DFS对应节点同质性。关于为什么BFS和DFS分别对应节点的结构相似性和同质性的讨论见知乎关于Node2vec算法中Graph Embedding同质性和结构性的进一步探讨。采用SkipGram方法对Graph提取表示。根据SkipGram的思路，重点在于定于上下文（Context），也就是Neighborhood。

为了将BFS和DFS结合，去融合发掘图中节点的两种相似性，采用一种二阶的方法Biased-random walk代替BFS和DFS，拥有两个参数p和q，来控制多大的概率反复经过一些Node和控制往回走和往前走。总之，整个Random Walk的目的就是在DFS和BFS之间采取某种平衡。

模型

优化目标

设 $f (u)$ 是将顶点 $u$ 映射为embedding向量的映射函数,对于图中每个顶点 $u$ ，定义 $N_{S}(u)$ 为通过采样策略 $S$ 采样出的顶点 $u$ 的近邻顶点集合。

node2vec优化的目标是给定每个顶点条件下，令其近邻顶点（如何定义近邻顶点很重要）出现的概率最大。
$\max _{f} \sum_{u \in V} \log \operatorname{Pr}\left(N_{S}(u) | f(u)\right)$
为了将上述最优化问题可解，文章提出两个假设：

条件独立性假设

假设给定源顶点下，其近邻顶点出现的概率与近邻集合中其余顶点无关。
$\operatorname{Pr}\left(N_{S}(u) | f(u)\right)=\prod_{n_{i} \in N_{S}(u)} \operatorname{Pr}\left(n_{i} | f(u)\right)$

特征空间对称性假设

这里是说一个顶点作为源顶点和作为近邻顶点的时候共享同一套embedding向量。(对比LINE中的2阶相似度，一个顶点作为源点和近邻点的时候是拥有不同的embedding向量的) 在这个假设下，上述条件概率公式可表示为
$\operatorname{Pr}\left(n_{i} | f(u)\right)=\frac{\exp \left(f\left(n_{i}\right) \cdot f(u)\right)}{\sum_{v \in V} \exp (f(v) \cdot f(u))}$