AVL 树-优快云博客

本文链接：https://blog.youkuaiyun.com/zjq_love/article/details/126243777

本文介绍了AVL树的基本概念，包括其定义、节点结构及插入操作的处理方式。AVL树是一种特殊的二叉搜索树，通过维护节点的平衡因子来确保树的高度平衡，从而实现高效的搜索。文章还详细讨论了四种不同的插入情况及其对应的旋转调整方法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

文章目录

AVL树的概念

一棵AVL树或者是空树，或者是具有以下性质的二叉搜索树：

它的左右子树都是AVL树
左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)

在这里插入图片描述
如果一棵二叉搜索树是高度平衡的，它就是AVL树。如果它有n个结点，其高度可保持在

$O(log_2 n)$ ，搜索时间复杂度O( $log_2 n$ )。

AVL树节点的定义

template<class Key,class Val>
struct AVLTreeNode
{
	AVLTreeNode<Key, Val>* _left;
	AVLTreeNode<Key, Val>* _right;
	AVLTreeNode<Key, Val>* _parent;
	pair<Key, Val> _kv;
	
	//平衡因子
	int _bf;


	AVLTreeNode(const pair<Key, Val>& kv)
		:_left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _kv(kv)
		,_bf(0)
	{}
};

AVL树的插入(难点)

AVL树就是在二叉搜索树的基础上引入了平衡因子，因此AVL树也可以看成是二叉搜索树。那么AVL树的插入过程可以分为两步：

按照二叉搜索树的方式插入新节点
搜索二叉树
调整节点的平衡因子

情况1：新节点插入较高左子树的左侧-进行右单旋
在这里插入图片描述

void RotateR(Node* cur)
	{
		Node* SubL = cur->_left;
		Node* SubLR = SubL->_right;
		//     60
		//  30
		//10
		Node* parent = cur->_parent;

		cur->_left = SubLR;
		if(SubLR)
			SubLR->_parent = cur;


		SubL->_right = cur;
		cur->_parent = SubL;


		if (parent == nullptr)
		{
			_root = SubL;
			SubL->_parent = parent;
		}
		else
		{
			if (parent->_left == cur)
			{
				parent->_left = SubL;
				SubL->_parent = parent;
			}
			else if (parent->_right == cur)
			{
				parent->_right = SubL;
				SubL->_parent = parent;
			}
			else
			{
				assert(false);
			}
		}

	}

情况2：新节点插入较高右子树的右侧-进行左单旋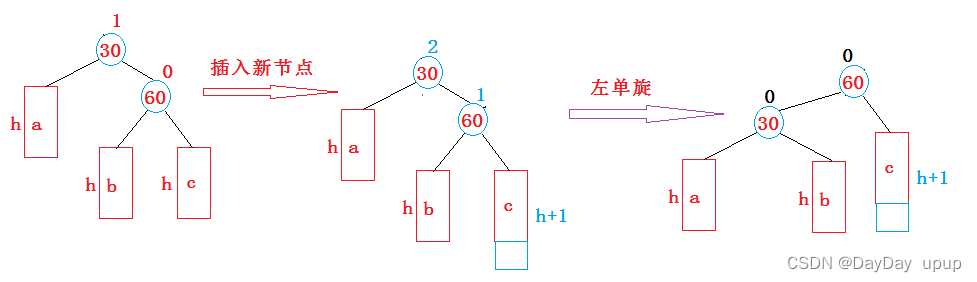在这里插入图片描述

void RotateL(Node* cur)
	{
		Node* SubR = cur->_right;
		Node* SubRL = SubR->_left;
		//10
		//  30
		//	   60
		Node* parent = cur->_parent;

		cur->_right = SubRL;
		if (SubRL)
			SubRL ->_parent = cur;


		SubR->_left = cur;
		cur->_parent = SubR;


		if (parent == nullptr)
		{
			_root = SubR;
			SubR->_parent = parent;
		}
		else
		{
			if (parent->_left == cur)
			{
				parent->_left = SubR;
				SubR->_parent = parent;
			}
			else if (parent->_right == cur)
			{
				parent->_right = SubR;
				SubR->_parent = parent;
			}
			else
			{
				assert(false);
			}
		}
	}

情况三：新节点插入较高左子树的右侧-先左单旋再右单旋
1.在b树插入新节点
在这里插入图片描述
2.在c树插入新节点

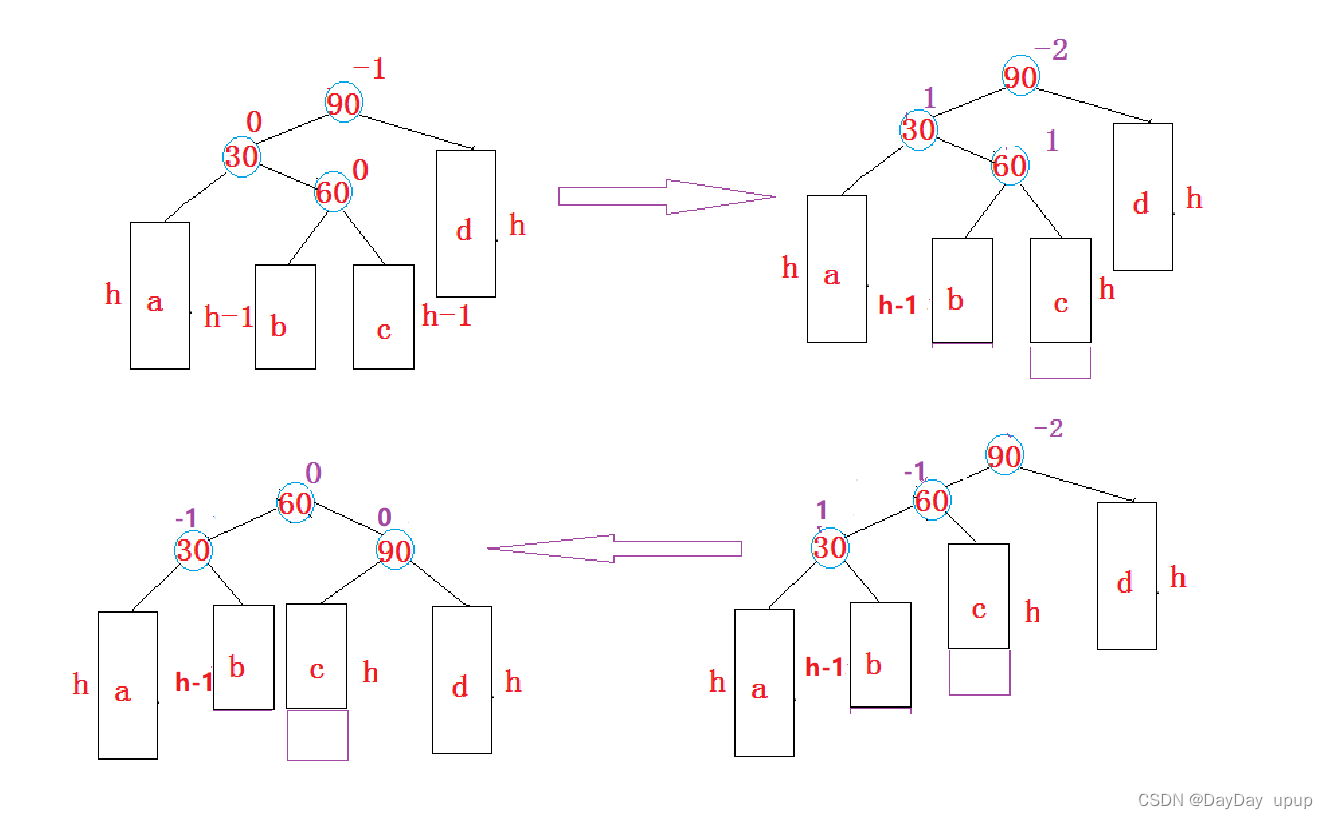
3.60即为插入的新节点

以上三种情况都是先左旋再右旋，区别：旋转完之后节点的平衡因子不同

		Node* node = cur->_right;
		int bf = node->_bf;
		RotateL(cur);
		RotateR(parent);

		if (bf == 0)
		{
			parent->_bf = cur->_bf = node->_bf = 0;
		}
		else if (bf == -1)
		{
			cur->_bf = node->_bf = 0;
			parent->_bf = 1;

		}
		else if (bf == 1)
		{
			parent->_bf = node->_bf = 0;
			cur->_bf = -1;
		}

情况4：新节点插入较高右子树的左侧-先右单旋再左单旋
在这里插入图片描述
与情况三相同，60的平衡因子会影响旋转完之后30 60 90 的平衡因子

	Node* node = cur->_left;
	int bf = node->_bf;
	RotateR(cur);
	RotateL(parent);
	if (bf == 0)
	{
		parent->_bf = cur->_bf = node->_bf = 0;
	}
	else if (bf == 1)
	{
		cur->_bf = node->_bf = 0;
		parent->_bf = -1;
	}

	else if (bf == -1)
	{
		node->_bf = parent->_bf = 0;
		cur->_bf = 1;
	}