搜索二叉树

概念

左子树上所有节点的值都小于根节点的值
右子树上所有节点的值都大于根节点的值
它的左右子树也分别为二叉搜索树

插入

搜索二叉树的插入比较简单
：若树为空，则直接增加节点给root指针
，若树不为空，则按照搜索二叉树的性质找到，空节点，在插入

	bool Insert(const T& key)
	{
		//root为空
		if (_root == nullptr)
		{
			_root = new Node(key);
			return true;
		}
		Node* cur = _root;
		Node* parent = nullptr;
		while (cur)
		{
			if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				return false;
			}
		}
		cur = new Node(key);
		//寻找插入位置
		if (parent->_key > key)
		{
			parent->_left = cur;
		}
		else if (parent->_key < key)
		{
			parent->_right = cur;
		}
		return true;
	}

删除（难点）

如果我们要删除7,6等叶节点，直接删除即可，但如果我们要删除2,5等非叶节点又应该如何做呢？

删除的结点可能分下面四种情况：
a. 要删除的结点无孩子结点
b. 要删除的结点只有左孩子结点
c. 要删除的结点只有右孩子结点
d. 要删除的结点有左、右孩子结点

情况b：删除该结点且使被删除节点的双亲结点指向被删除节点的左孩子结点–直接删除

删除2

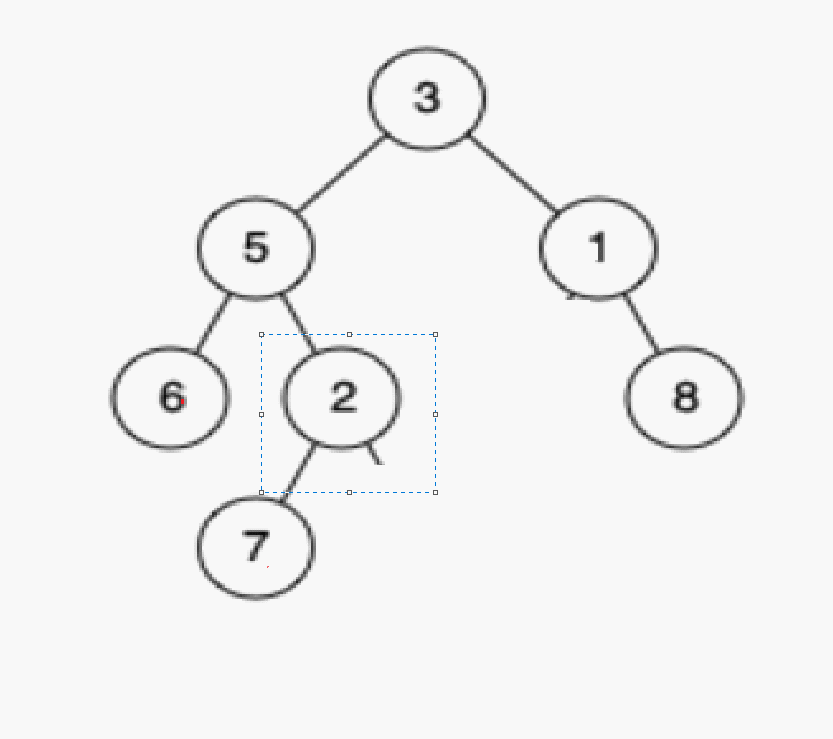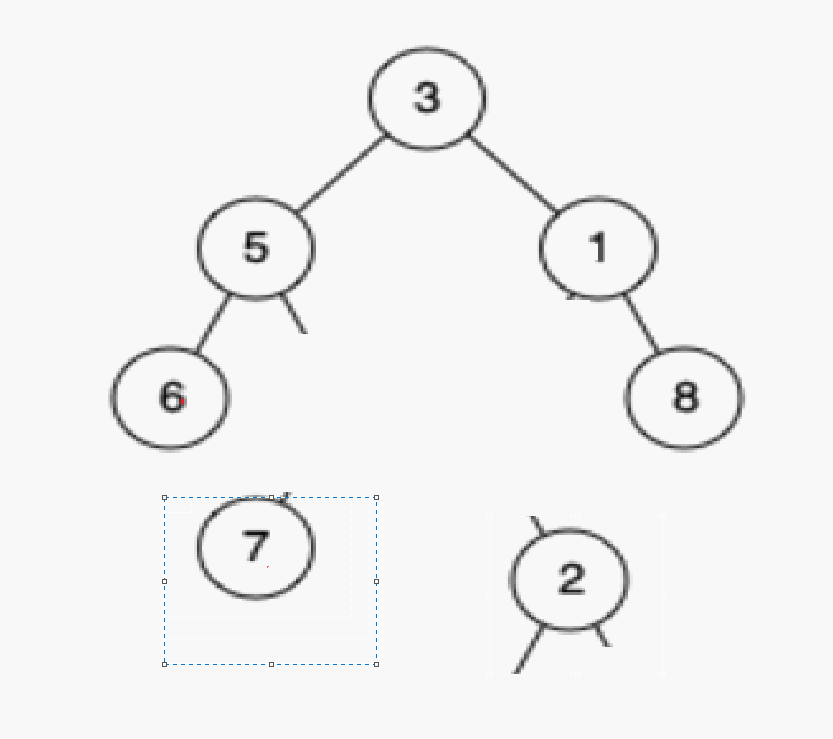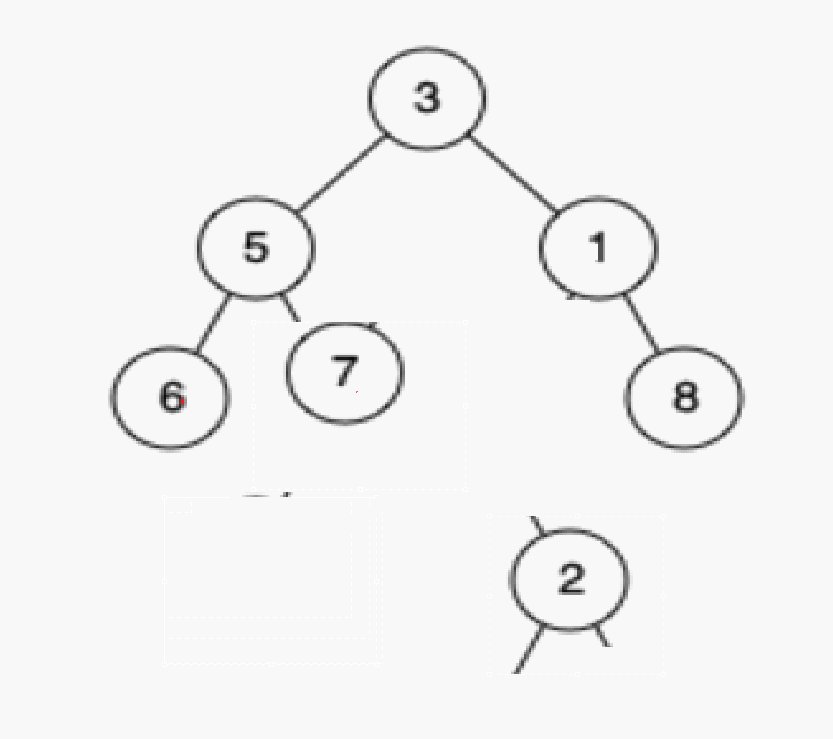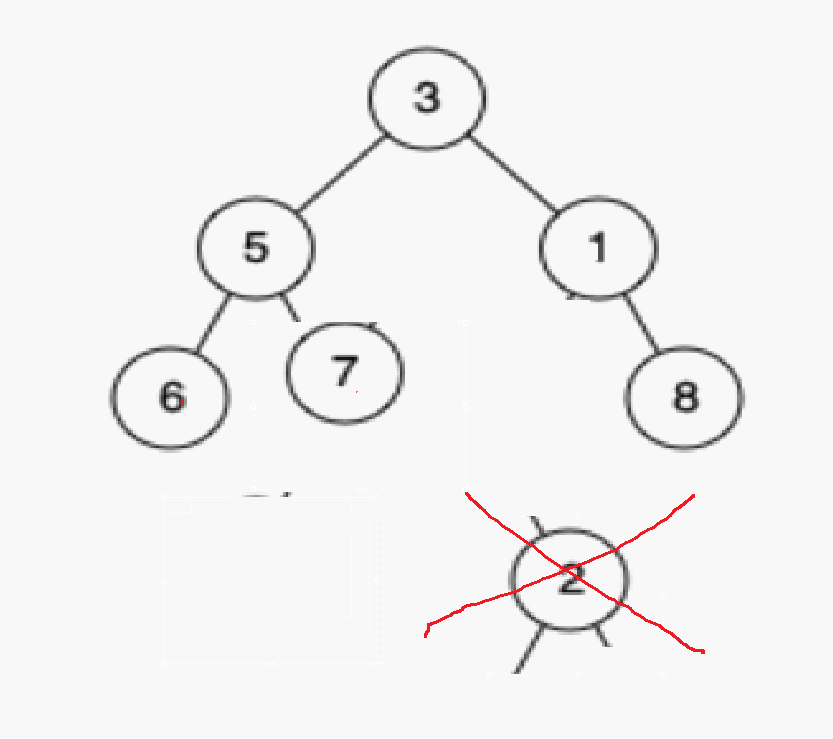
情况c：删除该结点且使被删除节点的双亲结点指向被删除结点的右孩子结点–直接删除

删除1

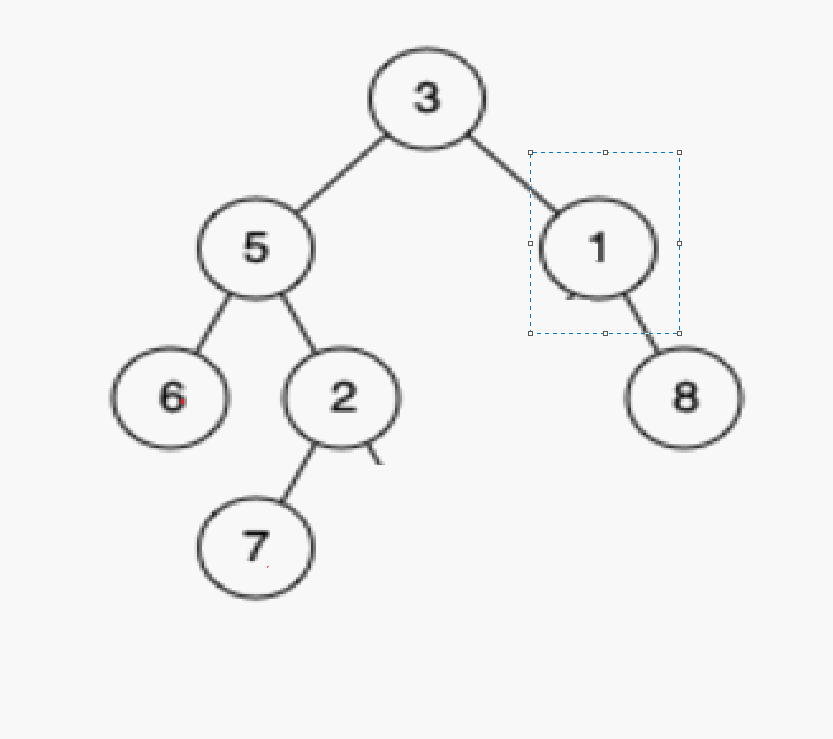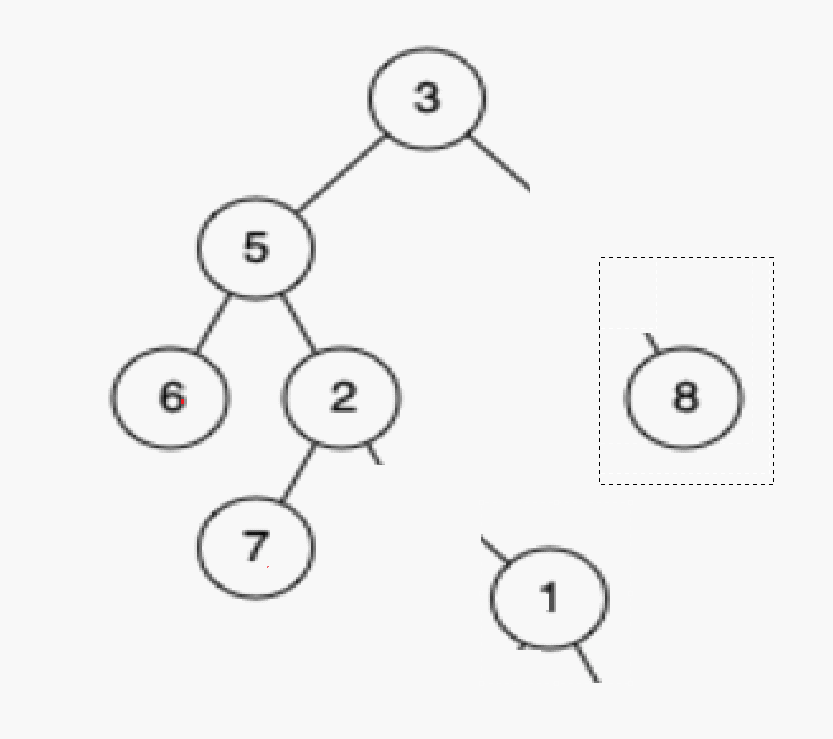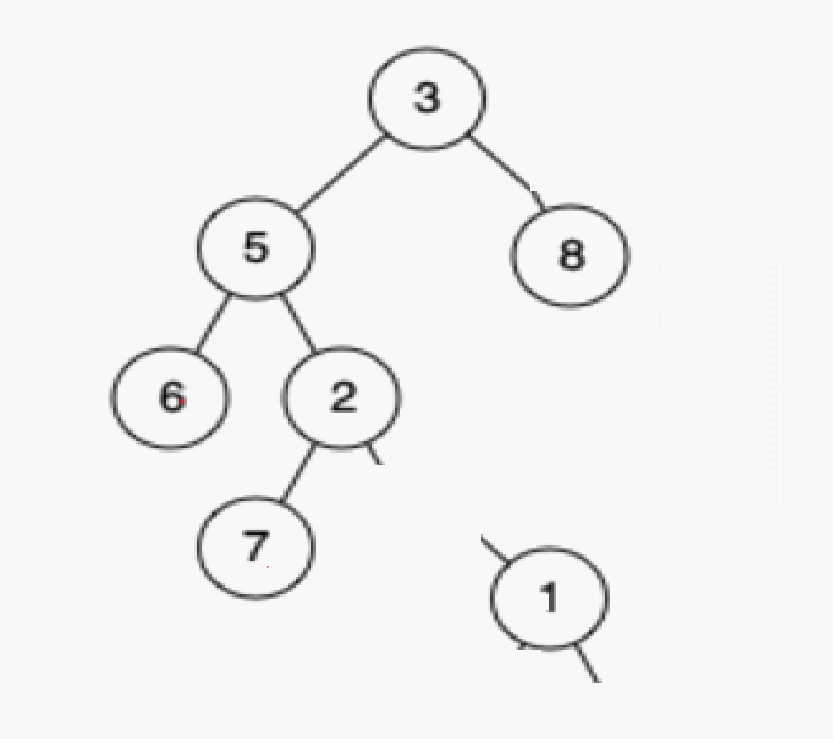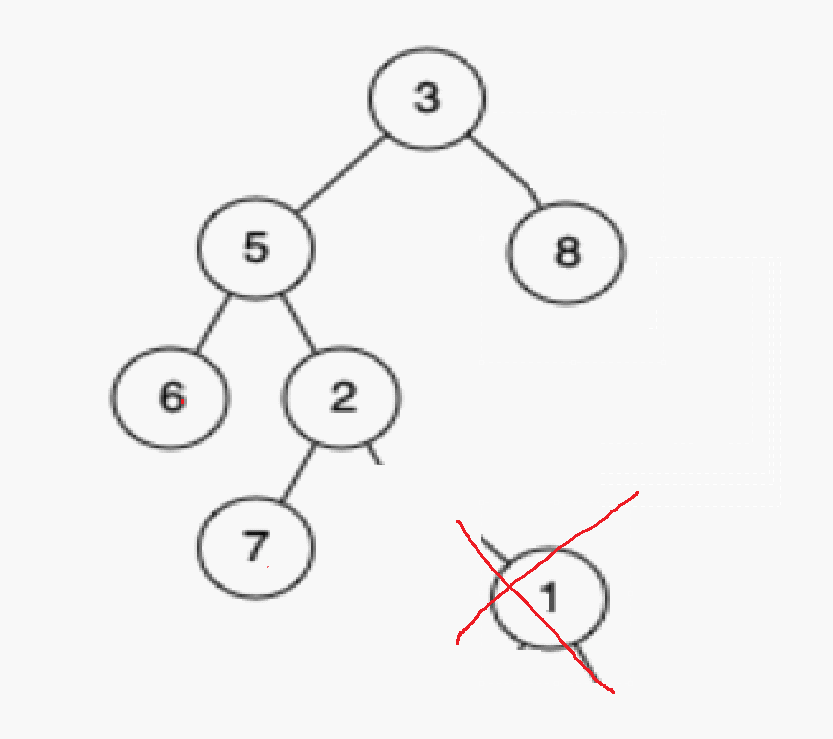
情况d：在它的右子树中寻找最大的节点，用它的值填补到被删除节点中，再来处理该结点的删除问题–替换法删除

删除5

	bool erase(const T& key)
	{
		Node* cur = _root;
		Node* parent = nullptr;
		while (cur)
		{
			if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				//cur左子树为空
				if (cur->_left == nullptr)
				{
					if (cur == _root)
					{
						_root = cur->_right;
					}
					else
					{
						if (parent->_left == cur)
						{
							parent->_left = cur->_right;
						}
						else
						{
							parent->_right = cur->_right;
						}
					}
		
					delete cur;
					return true;
				}
				//cur右子树为空

				else if (cur->_right == nullptr)
				{
					//cur为根
					if (cur == _root)
					{
						_root = cur->_left;
					}
					else
					{
						if (parent->_left == cur)
						{
							parent->_left = cur->_left;
						}
						else if (cur->_right == nullptr)
						{
							parent->_right = cur->_left;
						}
					}
					
					delete cur;
					return true;

				}

				//cur左右子树都不为空
				else
				{
					Node* Rightmin = cur->_right;
					Node* RightminParent = cur;
					while (Rightmin->_left)
					{
						RightminParent = Rightmin;
						Rightmin = Rightmin->_left;
					}

					cur->_key = Rightmin->_key;
					if (RightminParent->_left == Rightmin)
					{
						RightminParent->_left = Rightmin->_right;

					}
					else
					{
						RightminParent->_right = Rightmin->_right;
					}
					delete Rightmin;
				}

			}
		}
	}