【2018年南海区甲组】拆除桥墩(remove)

题目描述
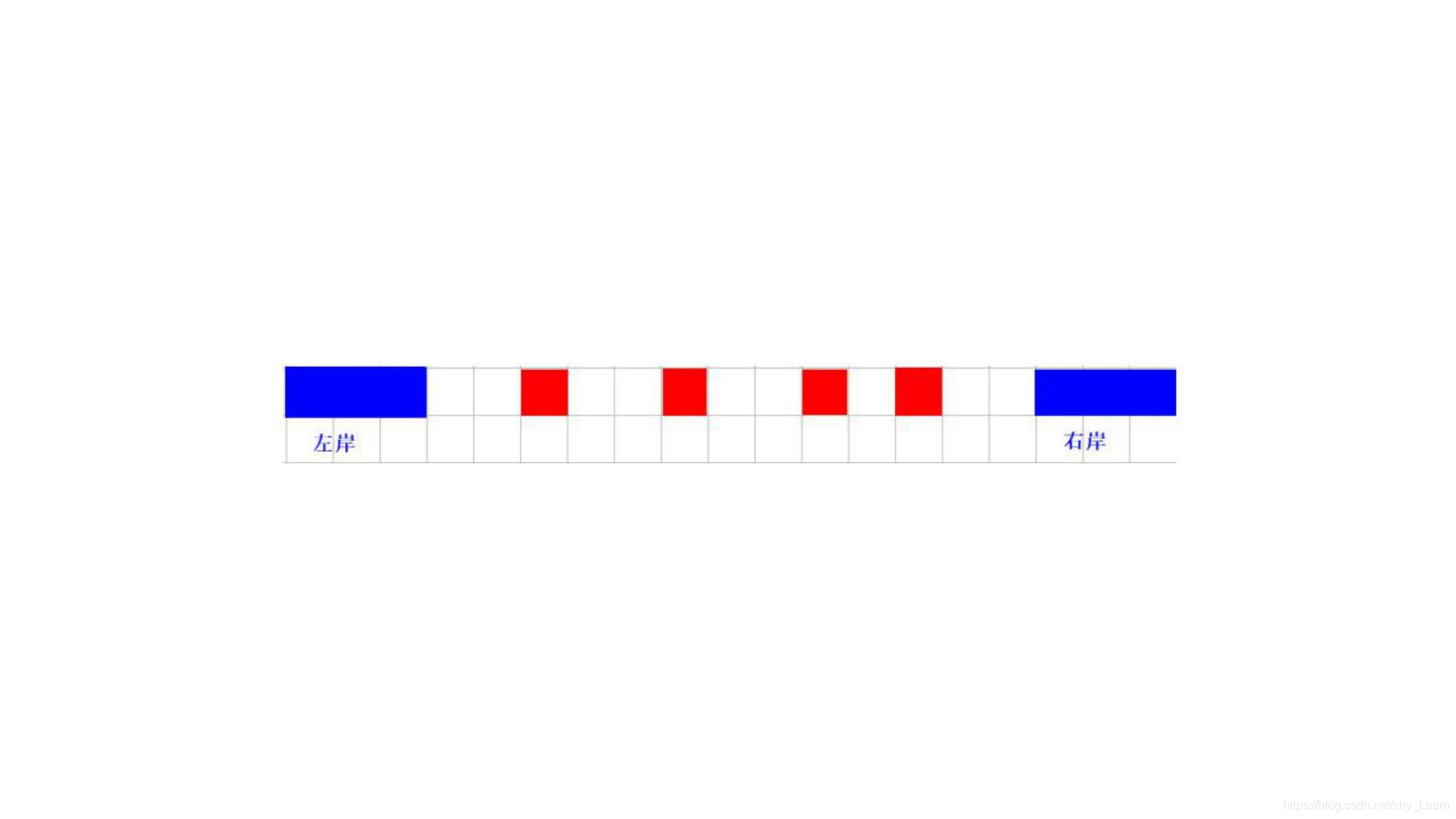
河的左岸到右岸之间有一座年久失修、已经废弃的大桥，有 N 个桥墩，影响船只通行。现在要拆除部分桥墩，使得通航能力最大，通航能力由最窄的地方决定的，这个地方有可能是岸与桥墩之间，也可以是桥墩之间。工程预算有限，只能拆除 M 个桥墩。如何安排工程，才能使得通航能力尽可能的大。

输入
第一行包含三个整数 L，N，M，分别表示左岸到右岸的距离、桥墩数和需要拆除的桥墩数。
接下来 N 行，每行一个整数，第 i 行的整数 Di（0 < Di < L）表示第 i 桥墩与左岸的距离。这些桥墩按与左岸距离从小到大的顺序给出。

输出
一个整数，为拆除了 M 个桥墩之后，最窄的地方最大值。

样例输入

24 4 2

2

11

17

21

样例输出

6

数据范围限制

0<=M <=N <=50000

1<=L<=1000000000

思路：二分查找
以前写过类似题的题解，大家点这看看，先了解一下二分。

看完后就，想想如何改动。
存位置的数组p1在前面加上0作为左岸，L作为右岸。

要留下的桥墩=N-M+2.（+2表示左右岸）；

了解后便可以对原上面这篇题解的原程序做改动。

代码：

#include<bits/stdc++.h>
using namespace std;
int n,m,k,p1[50005],mod,ans,r,l=1,a;
int S(int o){