【算法刷题】链表是否有环且输出入环节点--快慢指针法（JAVA）

【题目】LeetCode 142 linked-list-cycle II（环形链表）

【题址】https://leetcode-cn.com/problems/linked-list-cycle-ii/

【题干】

给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。

说明：不允许修改给定的链表。

示例 1：

输入：head = [3,2,0,-4], pos = 1

输出：tail connects to node index 1

解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：
输入：head = [1,2], pos = 0

输出：tail connects to node index 0

解释：链表中有一个环，其尾部连接到第一个节点。
 

示例 3：
输入：head = [1], pos = -1

输出：no cycle

解释：链表中没有环。

【思路】

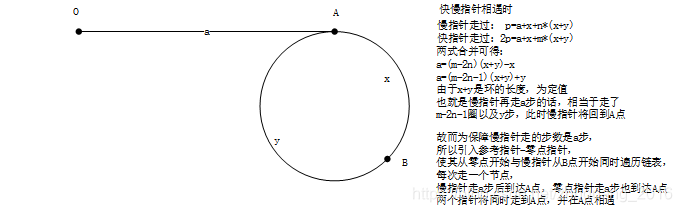
如图，先使用快慢指针相遇，识别链环，然后引入参考变量，零点指针计算环的入口节点
【程序】

	/**
	 * @author 白雪红叶约 2019.05.01 
	 * 【题目】142. linked-list-cycle-ii（链表是否有环,并输出入环节点） 
	 * 【思路】快慢指针法。
	 * 		 先使用快慢指针相遇，识别链环，然后引入参考变量，零点指针计算环的入口节点
	 * 		  快慢指针相遇时
	 *         慢指针走过： p=a+x+n*(x+y)
	 *         快指针走过：2p=a+x+m*(x+y)
	 *       两式合并可得：
	 *         a=(m-2n)(x+y)-x
	 *         a=(m-2n-1)(x+y)+y
	 *         由于x+y是环的长度，为定值。
	 *         也就是慢指针再走a步的话，相当于走了m-2n-1圈以及y步，此时慢指针将回到A点
	 *       故而为保障慢指针走的步数是a步，
	 *       所以引入参考指针-零点指针，使其从零点开始与慢指针从B点开始同时遍历链表，每次走一个节点，
	 *       慢指针走a步后到达A点，零点指针走a步也到达A点
	 *       两个指针将同时走到A点，并在A点相遇,此时零点指针指向节点即为环入口点。
	 * 【时间复杂度】O(n+k) 
	 * 【空间复杂度】O(1)
	 * @param head 原始链表头结点
	 * @return <ListNode> 入环节点或null
	 */
	public ListNode detectCycle1(ListNode head) {
		if (null == head || head.next == null)
			return null;
		ListNode fastNode = head.next.next;// 快指针
		ListNode slowNode = head.next;// 慢指针
		while (fastNode != slowNode) {
			if (fastNode == null || null == fastNode.next)
				return null;
			fastNode = fastNode.next.next;
			slowNode = slowNode.next;
		}
		//此时说明有环，然后构建零点指针，从零其与慢指针同步走，两者相遇时即为入环位置。
		ListNode zeroNode = head;// 新零指针
		while(zeroNode != slowNode) {
			zeroNode = zeroNode.next;
			slowNode = slowNode.next;
		}
		return zeroNode;
	}

【图解】

以 head = [1,2,3,4,5,6], pos = 3为例

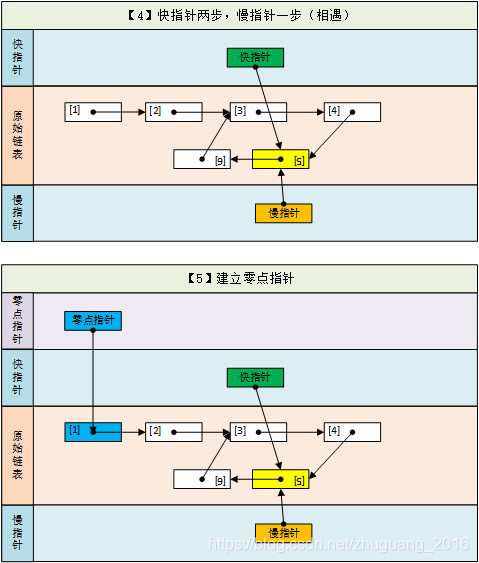
（0-1）初始化声明快慢指针并各自走出第一步

 ListNode fastNode = head.next.next;// 快指针
 ListNode slowNode = head.next;// 慢指针

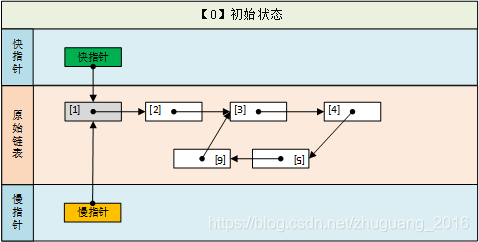
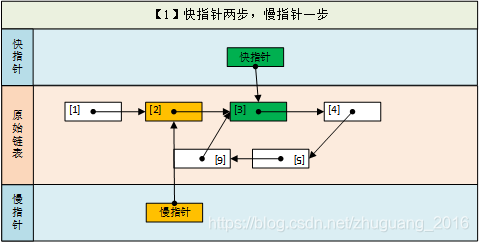
（2-3）快慢指针逐步遍历链表

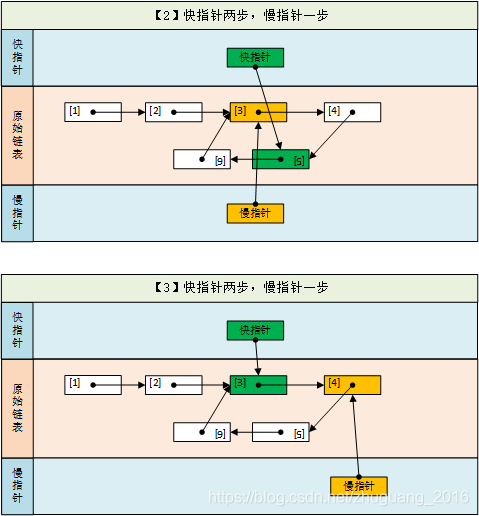
（4-5）当指针相遇时，说明存在环，建立零点指针。

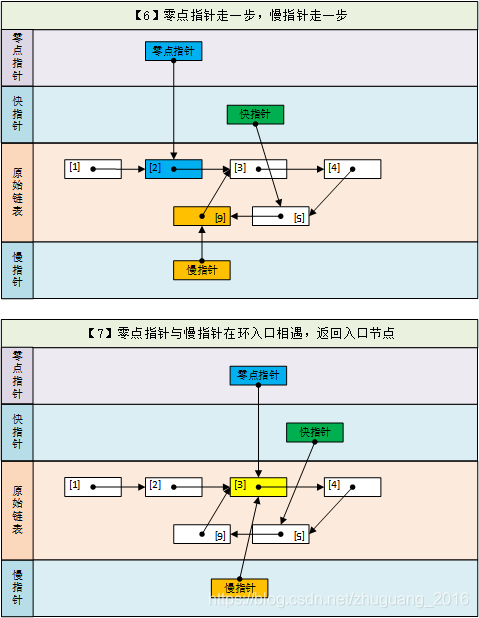
（6）零点指针与慢指针继续遍历，每次走相同步数（1步）