Roberson图与overlap

目录

一、Roberson图

二、Overlap

---

本文是介绍基4 SRT算法前的第二篇补充文章《Roberson图与overlap》。

一、Roberson图

J.E.Robertson是SRT算法中的“R”，Roberson图是其在最先发表的论文中描述以下公式的表示方法图：

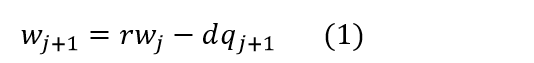
其中，

wj+1为下个部分和；

r为基；

wj为当前部分和；

d为除数；

qj+1为某次迭代产生的商数；

具体公式可参考之前文章：《除法器(3)——基2 SRT算法》

 

假设rw(j)=x，w(j+1)=y，重写上式：

y = x – d*q

当q=0, y = x

当q=1, y = x – d

当q=2, y = x – 2d

…

 

我们可以根据不同的q值描绘出很多个y和x关系的直线，比如下图：

Roberson图

商q从数字集{-a,-a+1,…,-1,0,1,…,a-1,a}中一一取值，画出所有曲线描述如上，即是Roberson图。

 

上期提到，对于基r，以下商集：

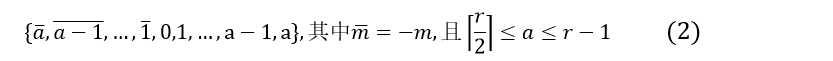
商集的冗余因子为：

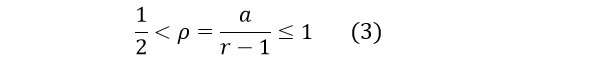
对于QDS函数，其目的在于选择出商值q，而其收敛的条件为：

则：

根据上图中可以看出：

其中q属于商集{-a,…,a}。

对于q的a和-a时：

又因为从上图中可以看出，

联立(8)、（9）、（10）、（11）式可得：

所以：

对于任意的wj，为保证其至少有一个商值可以选择,则必须满足：

所以:

我们在式（4）、（5）中限制了部分和的收敛条件，在式（14）、（15）中得出了商q的部分和乘基的选择范围。

二、Overlap

此处的overlap即是重合的区域。

我们来看对于q-1的选择。

对于q：

y = x – d*q

对于q-1

y = x – d*(q-1)

分别将以上两条曲线在Roberson图中画出，可以看出

从上图可以看出：

当x在橘色区域时，商的值可选为q-1；

当x在绿色区域时，商的值可选为q；

当x为加粗红色线段时，向y轴正方向，可选商值为q-1；也可向x轴负方向，可选商值为q，而这段区域即为重合区域。

式（17）说明了重合区域的大小取决于冗余因子和被除数的大小，重合区域对于P-D图至关重要，我们下期再介绍。

 

 

谢谢您的阅读！

更新不易，如果对您有帮助，记得点赞关注哦。欢迎批评指正，谢谢鼓励！

一起“纸上谈芯”，共同学习: