float的精度及其取值范围

float的存储方式

float在计算机中是用科学计数法的形式来存储的，科学计数法的表示方式是a.b*10^c，因为计算机中是用二进制来存储东西的，只有0和1这两个数，并且最大数为1，所以float的科学计数法为（+-）1.b*2^c，所以计算机只需要存储三部分就可以了（+-，b，c）

float的存储的空间是4字节（32位bite)，由符号位（1bite）、指数部分（7bite）、小数部分（32bite）。

1.Sign（1位）：用来表示浮点数是正数还是负数，0表示正数，1表示负数。

2.Exponent（8位）：指数部分，即上文提到数字c，取值范围为（-127）-128。

3.Mantissa（23位）：小数部分，也就是上文中提到的数字b。

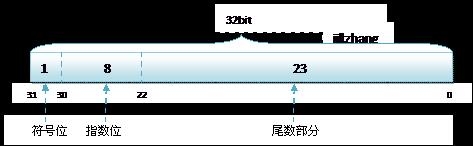
float存储示例

以数字6.5为例，看一下这个数字是怎么存储在float变量中的：

1.先来看整数部分，模2求余可以得到二进制表示为110。

2.再来看小数部分，乘2取整可以得到二进制表示为.1。

3.拼接在一起得到110.1然后写成类似于科学计数法的样子，得到1.101 x2^2。

4.从上面的公式中可以知道符号为正，尾数是101，指数是2。

5.符号为正，那么第一位填0，指数是2，加上偏移量127等于129，二进制表示为10000001，填到2-9位，剩下的尾数101填到尾数位上即可。

6.内存中二进制数01000000 11010000 00000000 00000000表示的就是浮点数6.5

这样说明一个问题，为什么指数部分要加上偏移量127，而不用byte存储类型来表示。

偏移量是什么?
叫移码.
使用偏移量的意义何在?
浮点数指数大小的比较结果变得显而易见. 
为什么呢?
因为负数的原码,反码,补码比正数的原码,反码,补码要大.
当直接比较两个浮点数指数大小时,会用一个1xxxxxx 来跟一个0xxxxxxx来比较，所以从表面看负数反而比正数大，这明显不是人类想要的结果，但如果引入偏移量127（0111 1111）,很容易比较出大小，我们下面来举几个例子。

十进制原码        原码                  移码                  float指数           十进制指数

0                  0000 0000             0111 1111          0111 1111               0

1                  0000 0001             0111 1111         1000 0000              1

2                  0000 0010             0111 1111         1000 0001               2

                                ----------------     

127              0111 1111              0111 1111         1111 1110               127

128             1000 0000              0111 1111         1111 1111               128

-1                1000 0001              0111 1111         0000 0000              -1
那为什么偏移量选127呢? 

移码就是真值加2^n构成的，8位移码表达0~255，所以表达的真值就是-128~127（真值+128变成对应的移码，1000 0000规定为-128（byte））
我们再来看一下float这个浮点数，23位尾数是原码表达，用来表达小数点后23位。那我们来考虑，浮点数怎么取到0，刚好0而不是近似0。注意，最小正值只能到2^(-126)，因为就算尾数全取0，前面还有一个隐藏位的1在啊，就算阶数取到最小，也是近似0而不是真正的0。所以IEEE那帮人就想了，那直接规定让阶数等于0的时候，隐藏位的1也变成0算了。
所以阶数全0，尾数全0，实际上是在表达0点。所以回到移码对应的真值数，我们发现-128表示不出来了，现在阶码的真值范围变成了-127~127。所以偏移量最大只能到达127，而不是128。
那么阶码127，真值为(127-127=0)的时候表示的是什么？当然就是1.m（尾数自己本身）。
很遗憾告诉你们一件事，刚刚的-127~127只是在移码的理想情况下证明为什么偏移量只能取127。实际上阶码的真值，也就是2的指数取值范围还要更小－－只有（-126~127），为什么呢？因为还有一个数（阶数全1）被用作浮点数表达正负无穷大和NaN了。阶数全1，尾数全0表达无穷大（正负性看数符），阶数全1，尾数不为0，是NaN。