软件编程中用到的数学是离散化的,而物理世界是连续的。把物理世界中连续性的方程表达式,转换成软件世界中离散形式是必须的。控制论中最重要的就是有关拉普拉斯变换的传递函数,只有把它变成离散形式(Z变换),这样才能用于编程(模拟实现)。下面打算一般形式的普拉斯变换的传递函数变成Z变换形式的数学原理做一下解释:(非本专业的人员可能看不懂,基本内容可以参考教材《自动控制原理(胡寿松版)》,好像教材中并没给出详细证明过程,决定补充一下这个证明过程)。
拉普拉斯变换与Z变换的关系(一)
题目1 证明如果连续函数f(t)的任意拉普拉斯变换为F(s),而且其的全部极点pi已知,则f(t)的Z变换F(z)为下式:
![]()
解:
存在下面公式
![]() (公式1)
(公式1)
对于信号采样,有下面公式
![]()
![]()
从而
![]()
或
![]()
![]() (公式2)
(公式2)
根据公式1,有:
![]()
代入公式2得到:
![]()
![]() (公式3)
(公式3)
<注:公式3中的z只与采样有关,而与积分时使用的s无关>
定义
![]()
则:
![]() (公式4)
(公式4)
对公式4两边同时乘上![]() 得到:
得到:
![]() (公式5)
(公式5)
公式4减去公式5得到
![]()
![]() (公式 6)
(公式 6)
将公式6代入公式3得到
![]()
![]()
![]()
![]()
证明上式用到闭曲线![]() ,
,
![]() 为直线段
为直线段![]() ,
,
![]() :
:
![]()
R充分大的时候,![]() 。
。
证明完毕。
另:对留数的计算(极点![]() 是m阶重极点)
是m阶重极点)
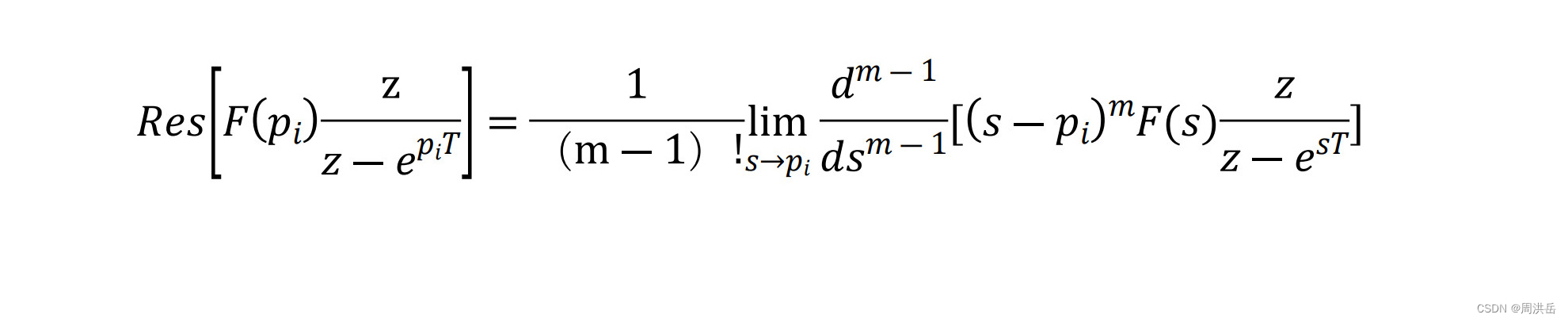






















 5358
5358

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










