电压源和电流源模型

目录
电压源和电流源模型
电流源的等效模型
一、理想电流源模型
二、实际电流源的等效模型（最常用）
三、其他等效模型（按应用场景细分）
四、核心结论
电压源的等效模型
一、理想电压源模型
二、实际电压源的等效模型（最常用）
三、其他等效模型（按应用场景细分）
四、核心结论

电压源和电流源模型

电流源的等效模型

电流源的等效模型是用于分析电路中电流源特性的简化电路表示，核心是通过 “理想电流源” 与 “内阻” 的组合，反映实际电流源的输出特性（如电流随负载的变化规律）。以下是电流源等效模型的详细解析：

一、理想电流源模型

理想电流源是理论上的理想器件，其核心特性为：
• 输出电流恒定：无论负载阻抗如何变化（在允许范围内），输出电流 IS 始终保持设定值，与负载两端的电压无关。
• 内阻无穷大：从电路模型角度，理想电流源的内阻 RCS=∞，因此负载阻抗的变化不会分流，确保输出电流全部流向负载。
符号与等效电路：
• 电路符号：通常用一个圆圈内标注电流方向和大小（如 IS）表示。
• 等效模型：仅包含理想电流源 IS，无其他元件。
适用场景：在简化电路分析（如忽略电流源内阻影响的理想情况下）时使用，例如分析基本放大电路的静态工作点时，可将偏置电流源视为理想电流源。

二、实际电流源的等效模型（最常用）

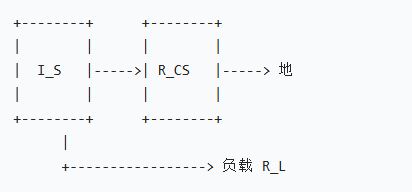
实际电流源的输出电流会随负载变化而略有波动，其等效模型需体现这一特性，由两部分组成：

1. 理想电流源 IS：代表电流源的标称输出电流（理想情况下的恒定值）。
2. 内阻 RCS：与理想电流源并联，模拟实际电流源因内部损耗导致的电流分流效应。
   模型特点：
   

• 当负载阻抗 RL 变化时，内阻 RCS 会分流部分电流，导致实际输出到负载的电流 IL 为：IL=IS×RCS+RLRCS
（推导：根据并联电路电流分配规律，总电流 IS 分为流过 RCS 的电流 ICS 和流过 RL 的电流 IL，即 IS=ICS+IL，且 ICS×RCS=IL×RL，联立可得上述公式。）
• 内阻 RCS 越大，分流效应越弱，实际输出电流 IL 越接近理想值 IS（恒流特性越好）。
符号与等效电路：
• 电路符号：与理想电流源相同，但需在分析中隐含并联内阻。
• 等效模型：理想电流源 IS 与内阻 RCS 并联（见下图示意）。

三、其他等效模型（按应用场景细分）

1. 考虑温度特性的模型
   实际电流源的输出电流会受温度影响（如半导体器件的温度系数），模型中可增加 “温度相关电流源” 或 “温度系数电阻”，表示为：IS(T)=IS0[1+α(T−T0)]
   
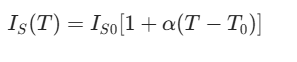
   其中 α 为温度系数，T0 为基准温度，用于分析温度变化对输出电流的影响（如高精度 DAC 中的电流源温漂补偿）。
2. 考虑噪声的模型
   电流源存在热噪声、散粒噪声等，等效模型中需在理想电流源两端并联 “噪声电流源”（功率谱密度为 2qIS，q 为电子电荷），或串联 “噪声电压源”（通过内阻转换为噪声电流），用于高精度电路的噪声分析。
3. 动态等效模型（高频场景）
   在高频应用中，电流源的寄生电容（如 MOS 管的结电容）不可忽略，模型中需增加并联电容 CCS，表示为：
   
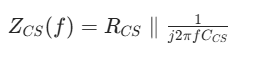
   ZCS(f)=RCS∥j2πfCCS1
   用于分析高频下电流源的输出阻抗变化及对电路带宽的影响。

四、核心结论

• 最基础且常用的电流源等效模型是 “理想电流源并联内阻”，它直观反映了实际电流源的恒流特性（内阻越大，恒流性能越好）。
• 复杂场景下（如温度敏感、高频、高精度），需增加温度系数、噪声源、寄生电容等元件，使模型更贴近实际器件特性。
• 等效模型的价值在于简化电路分析，通过它可快速计算负载变化对输出电流的影响、评估电流源的精度及稳定性。

电压源的等效模型

电压源的等效模型是用于分析电路中电压源特性的简化电路表示，核心是通过 “理想电压源” 与 “内阻” 的组合，反映实际电压源的输出特性（如输出电压随负载电流的变化规律）。以下是电压源等效模型的详细解析：

一、理想电压源模型

理想电压源是理论上的理想器件，其核心特性为：
• 输出电压恒定：无论负载电流如何变化（在允许范围内），输出电压 VS 始终保持设定值，与流过负载的电流无关。
• 内阻为零：从电路模型角度，理想电压源的内阻 RVS=0，因此负载电流的变化不会在内部产生压降，确保输出电压不受负载影响。
符号与等效电路：
• 电路符号：通常用一个圆圈内标注 “+”“-” 极性和电压值（如 VS）表示。
• 等效模型：仅包含理想电压源 VS，无其他元件。
适用场景：在简化电路分析（如忽略电压源内阻影响的理想情况下）时使用，例如分析基本串联电路的电流分配时，可将电池或稳压电源视为理想电压源。

二、实际电压源的等效模型（最常用）

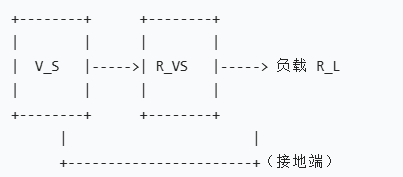
实际电压源的输出电压会随负载电流变化而略有波动（如电池放电时电压下降），其等效模型需体现这一特性，由两部分组成：

1. 理想电压源 VS：代表电压源的标称输出电压（理想情况下的恒定值）。
2. 内阻 RVS：与理想电压源串联，模拟实际电压源因内部损耗（如导线电阻、电源内部元件电阻）导致的电压降落。
   模型特点：
   

• 当负载电流为 IL 时，内阻 RVS 上的压降为 IL⋅RVS，因此实际输出到负载的电压 VL 为：
VL=VS−IL⋅RVS
• 内阻 RVS 越小，输出电压随负载电流的变化越平缓（带载能力越强），越接近理想电压源特性。
符号与等效电路：
• 电路符号：与理想电压源相同，但需在分析中隐含串联内阻。
• 等效模型：理想电压源 VS 与内阻 RVS 串联（见下图示意）。

三、其他等效模型（按应用场景细分）

1. 考虑温度特性的模型
   实际电压源的输出电压会受温度影响（如稳压管的温度系数），模型中可增加 “温度相关电压源”，表示为：
   
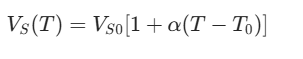
   VS(T)=VS0[1+α(T−T0)]
   其中 α 为温度系数，T0 为基准温度，用于分析温度变化对输出电压的影响（如高精度稳压电源的温漂补偿）。
2. 考虑噪声的模型
   电压源存在热噪声、低频噪声等，等效模型中需在理想电压源两端串联 “噪声电压源”（功率谱密度为 4kTR，k 为玻尔兹曼常数，T 为温度），用于高精度电路的噪声分析（如精密测量仪器的电源噪声评估）。
3. 动态等效模型（高频场景）
   在高频应用中，电压源的寄生电感（如电源引线电感）不可忽略，模型中需增加串联电感 LVS，表示为：
   
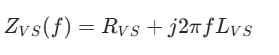
   ZVS(f)=RVS+j2πfLVS
   用于分析高频下电压源的输出阻抗变化及对电路稳定性的影响（如开关电源的高频纹波分析）。

四、核心结论

• 最基础且常用的电压源等效模型是 “理想电压源串联内阻”，它直观反映了实际电压源的带载特性（内阻越小，带载能力越强）。
• 复杂场景下（如温度敏感、高频、高精度），需增加温度系数、噪声源、寄生电感等元件，使模型更贴近实际器件特性。
• 等效模型的价值在于简化电路分析，通过它可快速计算负载电流变化对输出电压的影响、评估电压源的稳定性及带载能力。