概率分布与R语言

1、预备知识

概率：某事件发生的可能性的大小

随机变量：指变量的值无法预先确定仅以一定的可能性(概率)取值的量。它是由于随机而获得的非确定值，分为离散型随机变量（随机变量只能取有限个值）和连续型随机变量（随机变量可以取一个或多个区间中的任何值）。

离散型随机变量和连续型随机变量之间最根本的区别在于二者在概率计算上是不同的，对一个离散型随机变量，概率函数f(x)给出了随机变量x取某个特定值的概率，而对连续型随机变量，与概率函数相对应的是概率密度函数，也记做f(x)。不同的是，概率密度函数并没有直接给出概率，但是，通过给定区间上曲线f(x)下的面积给出连续型随机变量在该区间取值的概率，因此，当计算连续型随机变量的概率时，我们计算的是随机变量在某个区间内取值的概率。

随机变量的概率分布：描述随机变量取哪些值？取这些值的概率有多大？

分布律：也就是一个二维的表格，分别是随机变量和这个随机变量所对应的事件的概率，比如随机变量取值有0,1,2，每个随机变量对应的事件（可能一个随机变量对应多个事件）的概率分别0.1,0.5,0.4。则分布律的样子如下表：

X	0	1	2
P	0.1	0.5	0.4

由图可以知道，只有离散型的随机变量才会有分布律，连续型的随机变量取值太多了，根本没办法画出来。

分布函数：用于描述随机变量落在任一区间上的概率。如果将x看成数轴上的随机点的坐标，那么分布函数F(x)在x处的函数值就表示x落在区间(-∞，x)上的概率,分布函数也称为概率累计函数。

概率密度函数：指一个描述这个随机变量的输出值，在某个确定的取值点附近的可能性的函数。

关于分布函数和概率密度函数：

（1）概率密度函数只是针对连续性变量而言,而分布函数是对所有随机变量取值的概率的讨论,包括连续性和离散型；

（2）已知连续型随机变量的密度函数,可以通过讨论及定积分的计算求出其分布函数；当已知连续型随机变量的分布函数时,对其求导就可得到密度函数.
（3）对离散型随机变量而言,如果知道其概率分布（分布列）,也可求出其分布函数；当然知道其分布函数时也可求出概率分布。下图中，曲线是概率密度函数，阴影部分是分布函数。

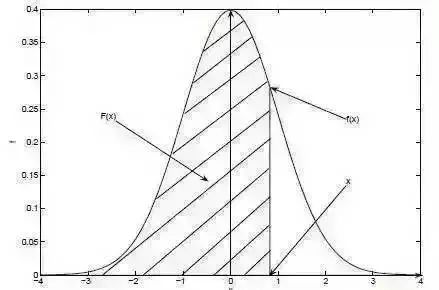
二、离散型随机变量常见的概率分布

离散型随机变量X只能取有限个可能的值x1,x2…，而且是以确定的概率取这些值的，即P（X=xi）=Pi(I=1,2…)，因此可以列出X的所有可能取值x1,x2^及每个值的概率p1,p2…，这就是离散型随机变量的概率分布，其基本性质是：

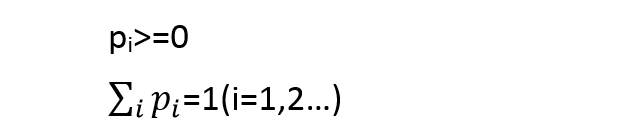
常见的分布有两点分布/（0-1)分布、等可能分布、二项分布、泊松分布、超几何分布等。

1、二项分布

二项分布是建立在伯努利试验的基础上，满足以下条件：

i.一次试验只有两个可能的结果，即成功和失败。

ii.一次试验成功的概率为p，失败的概率为1-p。

iii.试验是相互独立的，且可以重复进行n次。

在n次试验中，成功的次数对应一个离散型随机变量X，这样，在n次试验中，出现成功的次数的概率分布就是二项分布。

R中二项分布的概率函数为binom：

【产生随机样本】
rbinom(n, size, prob)