朴素贝叶斯

本文章参考：
周志华 《机器学习》
李航《统计学习方法》

---

很多人谈朴素贝叶斯都喜欢从它每个属性独立的特点来入手，我更想写写朴素贝叶斯的来源，也就是说，为什么我们需要它假设每个属性独立。

贝叶斯决策论

贝叶斯决策论其实就是基于概率的一种决策方法，说白了核心原理就是我们概率论中学的贝叶斯公式。

贝叶斯决策论的目的是最小化总体风险。我们面对一个分类问题，假设可能的类别有n种，针对一个新的样本x，它被分到哪一个类都有概率，我们需要的是让他被分到错误的n-1个类的总概率最小。

$$R(c_{i}|x)=\sum_{j=1}^{n}\lambda_{ij}P(c_{j}|x)$$
其中
$$\lambda_{ij}=\begin{cases} & \text 0 \ \ \ \ when \ i=j \\ & \text 1 \ \ \ \ when \ i\neq j \end{cases}$$
$\lambda$可以把样本分到正确类的概率筛出去，留下的是分到错误累的概，我们使它最小即可。
最小化其实非常简单，我们只需要在样本上选择那个能使得条件风险$R(c|x)$最小的类别标记，公式表达为：
$$h^{*}(x)=arg min R(c|x)$$
此时$h^{*}$称为贝叶斯最优分类器，这个分类器其实只是蕴含着一个分类规则而已。与之对应的整体风险就叫做贝叶斯风险，$1-R(h^{*})$反映了分类器所能达到的最好性能。此时我们的条件风险可以表达为：
$$R(c|x)=1-P(c|x)$$
我们和最优分类器的公式结合一下：
$$h^{*}(x)=argmaxP(c|x)$$
现在就非常直观了，我们最优分类器要找的就是它后验概率最大的类别标记。（说白了就是它最有可能属于哪类嘛）

现在的问题就是我们要知道$P(c|x)$怎么去求。两种方法，第一种是判别式模型，就是直接对$P(c|x)$条件概率进行建模。第二种是生成式模型，生成式模型先对联合概率分布建模，然后根据贝叶斯公式获得$P(c|x)$。

举个通俗点的例子，我们要判断一棵树是苹果树还是梨树还是樱桃树，判别式模型就是根据特征建一个苹果树模型，丢进去一个样本然后出来它是苹果树的概率是多少。生成式模型就是分别建立，计算他是每一颗树的概率，然后将结果判别为概率最大的那一类。

贝叶斯分类器用的是后者。

既然贝叶斯判定用的是后者那我们就要考虑联合概率分布了，贝叶斯公式如下：

$$P(c|x)=\frac{P(c)P(x|c)}{P(x)}$$
对于给定样本，证据因子P(x)肯定是都一样的，所以我们需要考虑的就是先验概率$P(c)$和类条件概率$P(x|c)$。

先验概率直接从训练样本中数数求出来就行，难的是类条件概率的求法。

类条件概率不能直接根据训练样中的频率信息来数，因为有些样本可能并没有在训练样本中出现。样本的特征有多种取值的话，排列组合出的情况有可能超出样本数，这样就会有未出现在训练样本中的情况，因此直接计算出的概率也不准确。西瓜书上的话就非常直观，“未被观测到“和“出现的概率为零“是不同的。

此时我们应该初见端倪，求类条件概率的难点在于样本的属性是相互有联系的，这样想求条件概率就只能在样本量及其大的情况下遍历所有组合。但如果属性之间相互独立，也就是说每个属性对所属分类标签的影响都是独立的，类条件概率就可以编程离散相乘的形式。

此时贝叶斯公式变成如下：

$$P(c|x)=\frac{P(c)P(x|c)}{P(x)}=\frac{P(c)}{P(x)}\prod_{i=1}^{d}P(x_{i}|c)$$
证据因子和先验概率都可以直接求出，变数就出现最后的累乘形式上。所以我们分类器的表达式就变为：
$$h(x)=argmaxP(c)\prod_{i=1}^{d}P(x_{i}|c)$$
此时分类器叫朴素贝叶斯分类器表达式。

其实非常容易理解了，朴素贝叶斯的目的在于算出每一个属性（特征）对类别的影响大小（概率），当面对新样本时，将新样本的属性取值对照着之前算出的概率累乘，取累乘结果最大的类别作为判别类别。

$$P(c)=\frac{|D_{c}|}{|D|}$$
其中$|D_{c}|$表示D中第c类样本组成的集合。
$$P(x_{i}|c)=\frac{|D_{c,x_{i}}|}{|D_{c}|}$$
$D_{c,x_{i}}$表示$D_{c}$中第i个特征上取值为$x_{i}$的样本组成的集合。

当特征取值不是离散的而是连续的时候就条件概率就不能这样直接算，需要假设他的取值符合高斯分布，我们只需计算出第i个属性在c类别上的均值$\mu _{c,i}$和方差$\sigma^{2}_{c,i}$，就会有：

$$P(x_{i}|c)=\frac{1}{\sqrt{2\pi}\sigma^{2}_{c,i}}exp(-\frac{(x_{i}-\mu _{c,i})^{2}}{2\sigma^{2}_{c,i}})$$

以上便是朴素贝叶斯算法的基本求解方法。但这样还有一个问题，条件概率是可能出现0的，这样累乘就变成了0，这相当于因为一个特征就抹去了其他所有特征的贡献，遇到这样的情况需要进行“平滑处理“，常用“拉普拉斯修正“，以下为修正方法。

$$P(c)=\frac{|D_{c}+1|}{|D|+N}$$ $$P(x_{i}|c)=\frac{|D_{c,x_{i}}|+1}{|D_{c}|+N_{i}}$$
其中N为类别的数量，$N_{i}$表示第i个特征的取值数。
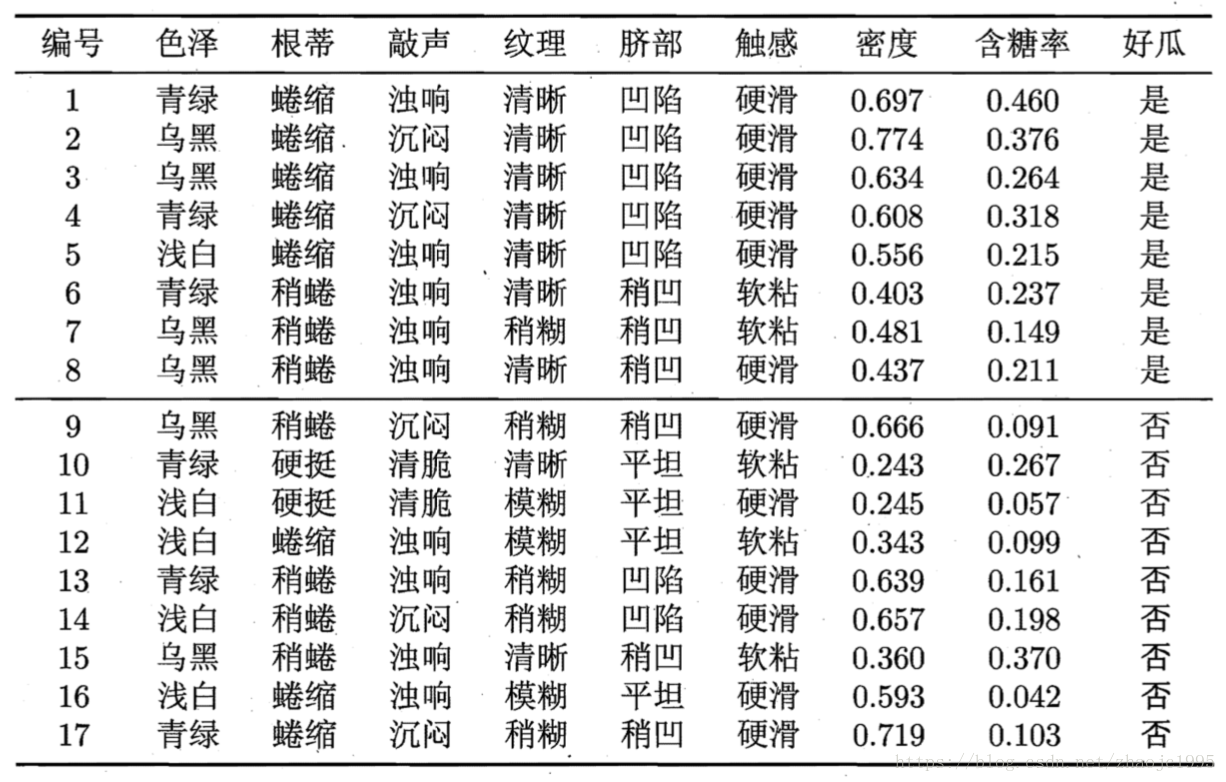
下面来搬运一段西瓜书上的例子来加理解：

sklearn中的朴素贝叶斯