7/8 每日刷题 递推求解（线性dp）

递推求解作为dp的一种特殊情况，递推求解可能不存在最优子结构，他的子结构只有一种情况。

递推求解更像思维题，也比较考验问题的分类方式。

hdu 2044 一只小蜜蜂... http://acm.hdu.edu.cn/showproblem.php?pid=2044

 

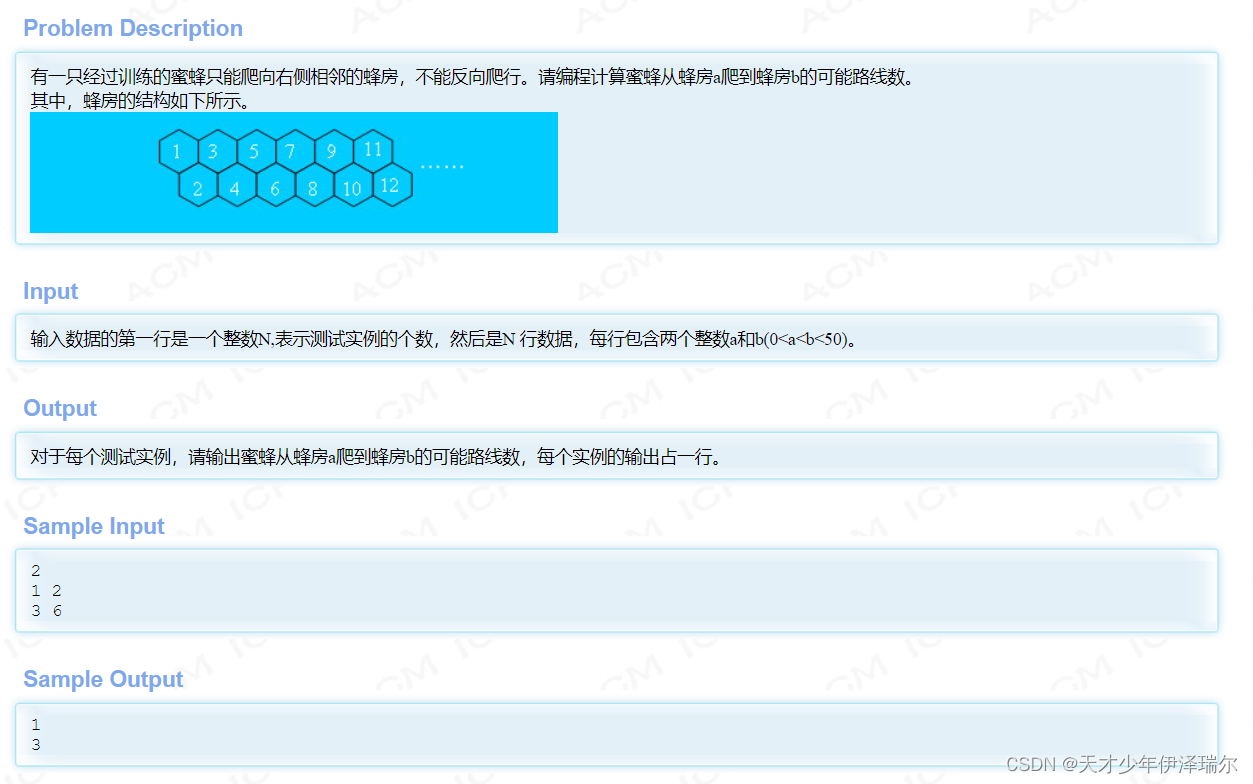
如果以F[]数组记录路线数的话，状态转移方程显而易见是F[i]=F[i-1]+F[i-2];这个不就是斐波那契数列嘛，预处理F数组，输出F[b-a]即可。

 

// Problem: 一只小蜜蜂...
// Contest: HDOJ
// URL: https://acm.hdu.edu.cn/showproblem.php?pid=2044
// Memory Limit: 65 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)

#include <bits/stdc++.h>

using namespace std;

long long f[55];

int main()
{
    f[1] = 1;
    f[2] = 2;
    for (int i = 3; i <= 50; i++)
    {
        f[i] = f[i - 1] + f[i - 2];
    }
    int t;
    cin >> t;
    while (t--)
    {
        int a, b;
        cin >> a >> b;
        printf("%lld\n", f[b - a]);
    }
}

hdu 2018 母牛的故事 http://acm.hdu.edu.cn/showproblem.php?pid=2018 

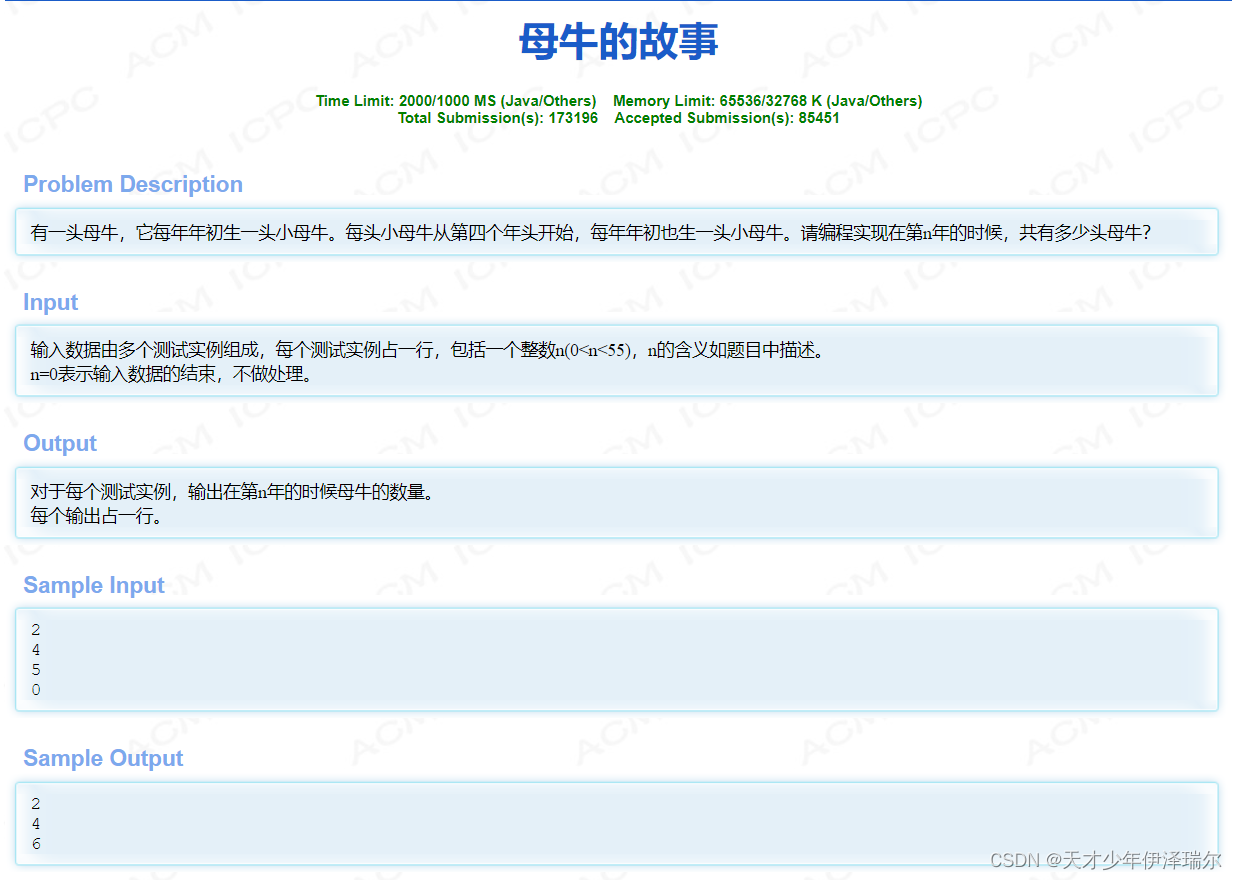
还是以一维数组f记录第几年时奶牛的总数，那么下一年的奶牛总数=今年的奶牛总数+新增的奶牛总数，新增的奶牛总数是今年已经成年的奶牛总数，小母牛在出生后的第四年那年成年，所以今年已经成年的奶牛总数是三年前的奶牛总数。

于是就有状态转移方程f[i]=f[i-1]+f[i-3],预处理输出对应f[n]即可~

#include<bits/stdc++.h>
using namespace std;

int f[55];
int main()
{
	f[1]=1;
	f[2]=2;
	f[3]=3;
	f[4]=4;
	for(int i=5;i<55;i++)
	{
		f[i]=f[i-1]+f[i-3];
	}
	int n;
	while(cin>>n,n)
	{
		printf("%d\n",f[n]);
	}
}

hdu 2045 不容易系列之(3)—— LELE的RPG难题 http://acm.hdu.edu.cn/showproblem.php?pid=2045

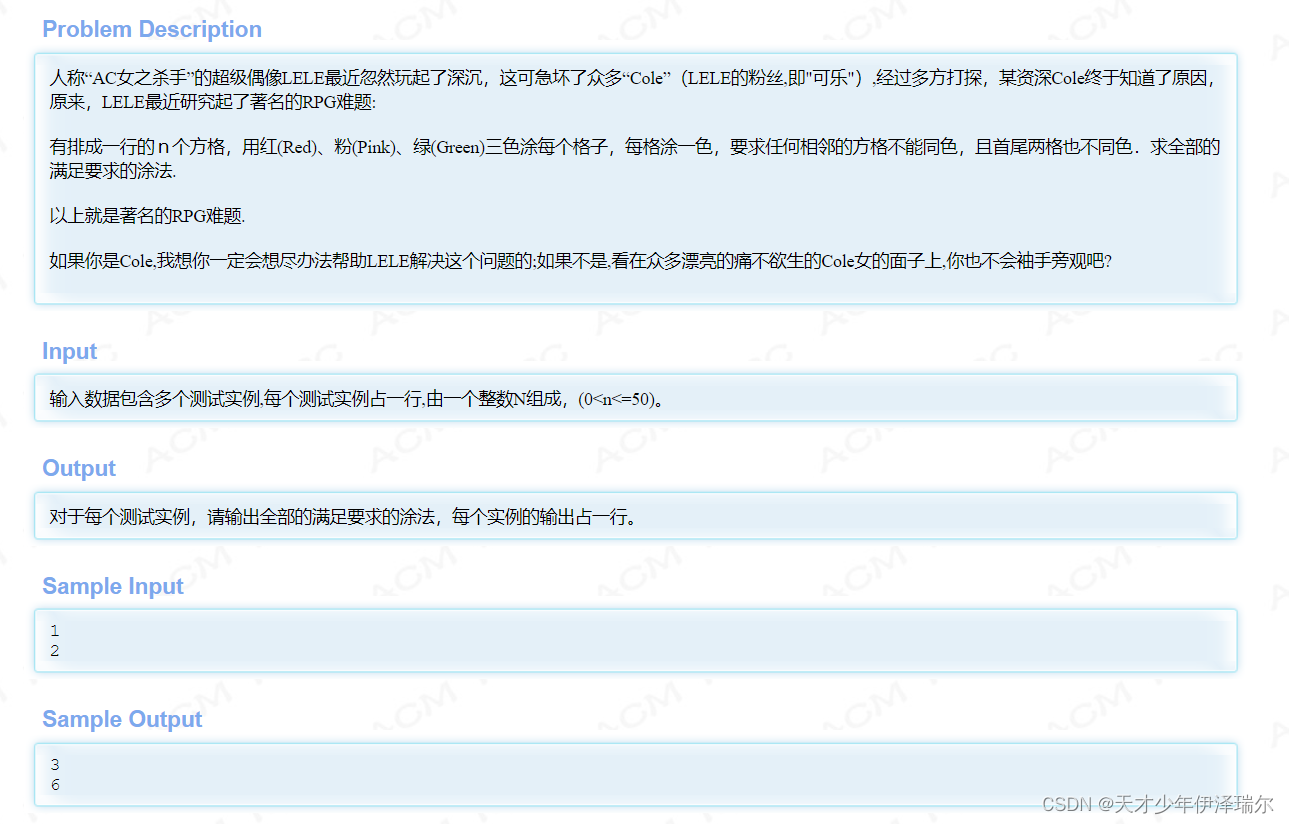
定义一维数组F[]，以F[n]表示前n个格子合法的情况，考虑第一个和倒数第二个格子是否同色，如果不同色，那么最后一个格子的颜色一定固定了此时有F[n-1]中涂法，如果第一个格子和倒数第二个格子同色，那么最后一个格子可以选两种颜色，又由于第一个格子和倒数第二个格子颜色相同，所以倒数第三个格子的涂法与倒数第二个格子不存在时是一样的，那么此时就有2*f[n-2]种涂法，要注意的是，这两种情况只在格子数大于等于4时成立（从分析过程可以看出）

于是就有状态转移方程f[n]=f[n-1]+2*f[n-2] (n>=4)

// Contest: HDOJ
// URL: https://acm.hdu.edu.cn/showproblem.php?pid=2045
// Memory Limit: 65 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)

#include <bits/stdc++.h>

using namespace std;

long long f[55];

int main()
{
    f[1] = 3;
    f[2] = 6;
    f[3] = 6;
    for (int i = 4; i <= 50; i++)
    {
        f[i] = f[i - 1] + 2 * f[i - 2];
    }
    int t;
    while (cin >> t)
    {
        printf("%lld\n", f[t]);
    }
}

hdu 2046 骨牌铺方格 http://acm.hdu.edu.cn/showproblem.php?pid=2046

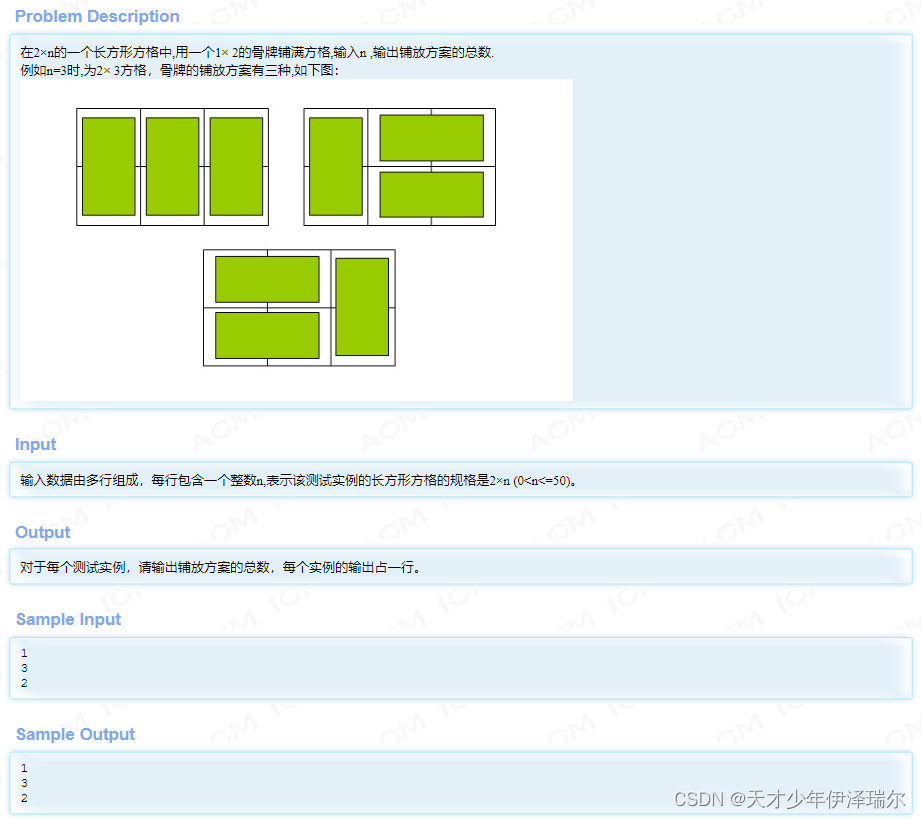
 方格的特点是，宽度固定为2，长度不定，定义一维数组f[],f[n]表示长度为n的方格铺满的方案数，我们考虑以方格右上角的正方形为分类依据，可以用一个竖着摆的骨牌覆盖这个正方形，其他方格的覆盖方式就是f[n-1]，也可以用一个横着摆的骨牌覆盖这个正方形，那么它的下面一行没得选只能是横着摆一个骨牌，其他方格的覆盖方式就是f[n-2]。

所以状态转移方程就是f[n]=f[n-1]+f[n-2];

// Contest: HDOJ
// URL: https://acm.hdu.edu.cn/showproblem.php?pid=2045
// Memory Limit: 65 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)

#include <bits/stdc++.h>

using namespace std;

long long f[55];

int main()
{
    f[1] = 3;
    f[2] = 6;
    f[3] = 6;
    for (int i = 4; i <= 50; i++)
    {
        f[i] = f[i - 1] + 2 * f[i - 2];
    }
    int t;
    while (cin >> t)
    {
        printf("%lld\n", f[t]);
    }
}