本文详细介绍了红黑树的基本概念、旋转操作、插入与删除过程及其修复方法。红黑树是一种自平衡二叉查找树，通过特定的旋转和重新着色操作保持平衡。
一：基本概念
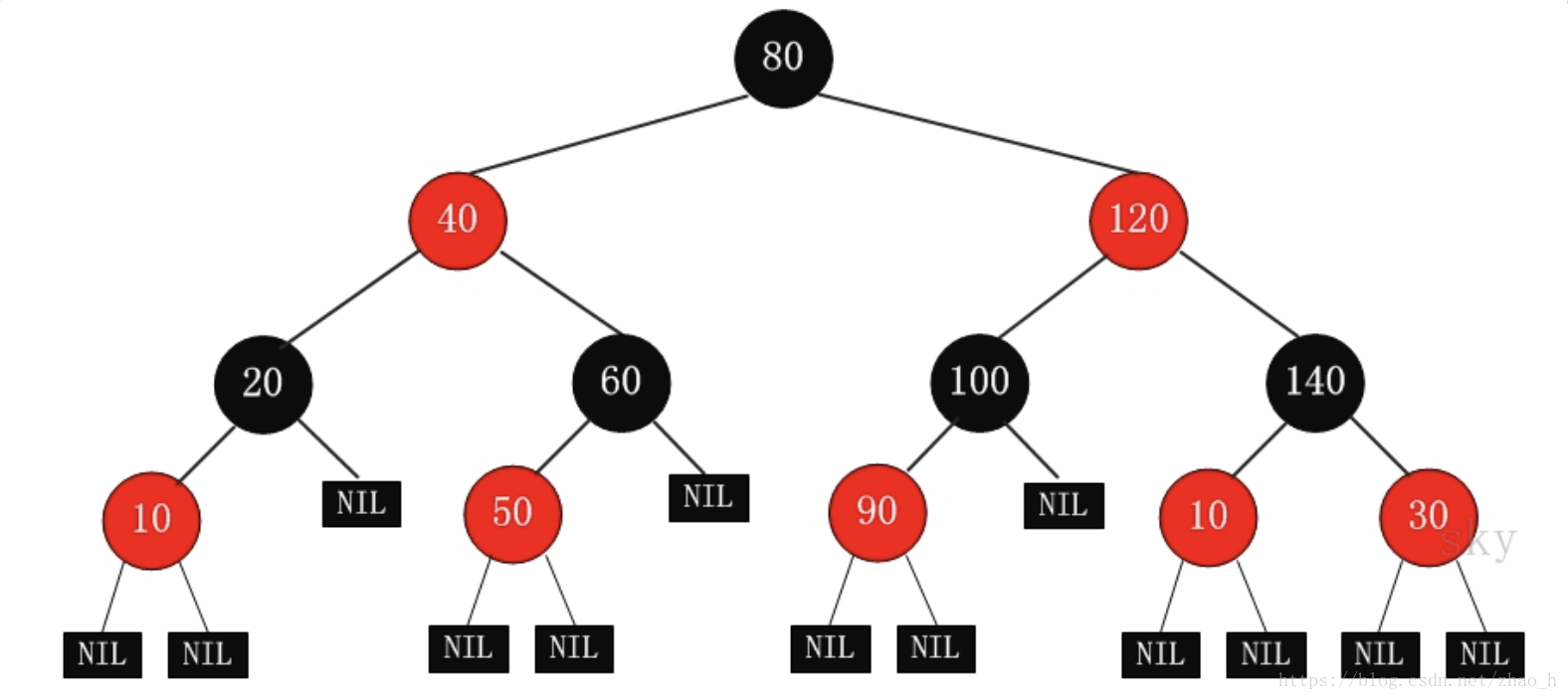
红黑树（Red Black Tree）：是一棵二叉搜索树，树中的每一个节点是红色或者黑色。
扩充二叉树：在二叉树中出现空子树的位置增加空树叶的二叉树，增加的空树叶叫外部节点。
红黑树的其他性质可以用扩充二叉树来说明：
1.根结点和所有外部节点都是黑色的；
2.在根结点至外部节点的路径上，没有连续的两个红色节点；
3.从一个节点到它所能到达的外部节点的路径上的黑色节点数都相同。
二：红黑树的旋转
在插入节点或删除节点操作之后，红黑树的性质都有可能发生改变，旋转操作可以恢复红黑树的性质。旋转分为左旋和右旋。
1.左旋
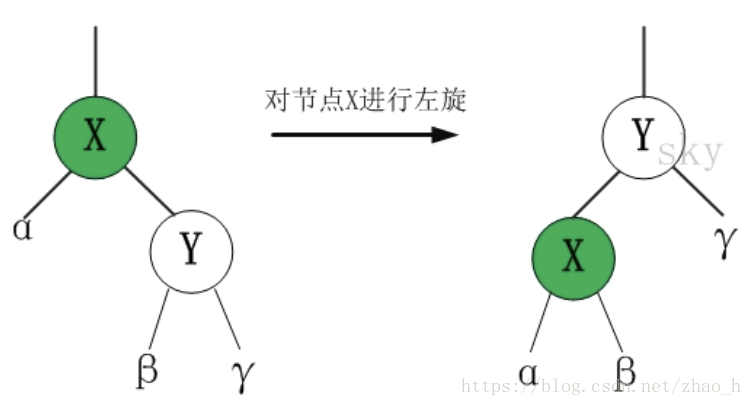
《算法导论》中左旋的伪代码如下：
左旋的伪代码
LEFT-ROTATE(T, x)
y ← right[x] // 前提：这里假设x的右孩子为y。下面开始正式操作
right[x] ← left[y] // 将 “y的左孩子” 设为 “x的右孩子”，即 将β设为x的右孩子
p[left[y]] ← x // 将 “x” 设为 “y的左孩子的父亲”，即 将β的父亲设为x
p[y] ← p[x] // 将 “x的父亲” 设为 “y的父亲”
if p[x] = nil[T]
then root[T] ← y // 情况1：如果 “x的父亲” 是空节点，则将y设为根节点
else if x = left[p[x]]
then left[p[x]] ← y // 情况2：如果 x是它父节点的左孩子，则将y设为“x的父节点的左孩子”
else right[p[x]] ← y // 情况3：(x是它父节点的右孩子) 将y设为“x的父节点的右孩子”
left[y] ← x // 将 “x” 设为 “y的左孩子”
p[x] ← y // 将 “x的父节点” 设为 “y”2.右旋
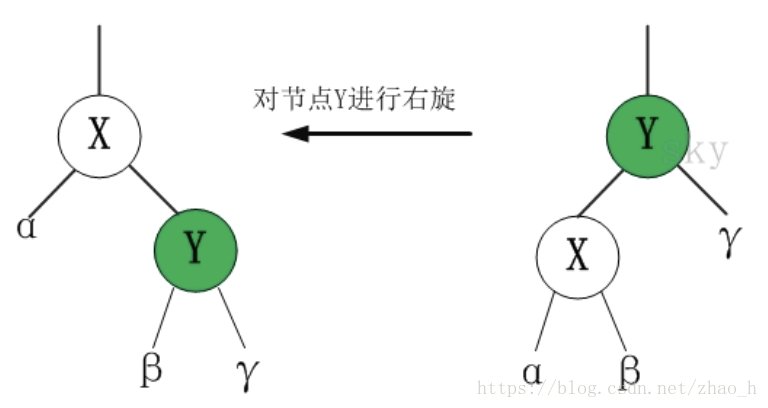
《算法导论》中右旋的伪代码如下：
右旋的伪代码：
RIGHT-ROTATE(T, y)
x ← left[y] // 前提：这里假设y的左孩子为x。下面开始正式操作
left[y] ← right[x] // 将 “x的右孩子” 设为 “y的左孩子”，即 将β设为y的左孩子
p[right[x]] ← y // 将 “y” 设为 “x的右孩子的父亲”，即 将β的父亲设为y
p[x] ← p[y] // 将 “y的父亲” 设为 “x的父亲”
if p[y] = nil[T]
then root[T] ← x // 情况1：如果 “y的父亲” 是空节点，也就是说原来的y是根结点，则将x设为根节点
else if y = right[p[y]]
then right[p[y]] ← x // 情况2：如果 y是它父节点的右孩子，则将x设为“y的父节点的左孩子”
else left[p[y]] ← x // 情况3：(y是它父节点的左孩子) 将x设为“y的父节点的左孩子”
right[x] ← y // 将 “y” 设为 “x的右孩子”
p[y] ← x // 将 “y的父节点” 设为 “x”3.左旋和右旋
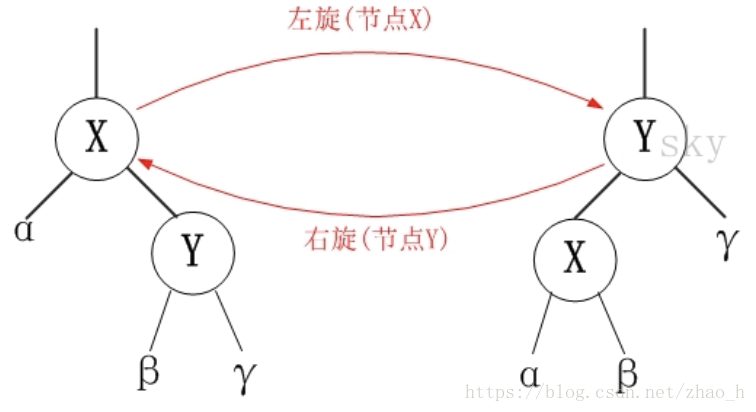
左旋意味着被旋转的节点成为左节点，右旋意味着被旋转的节点成为右节点。
三：红黑树的插入
步骤：
1.插入节点（二叉搜索树的插入操作）
2.着红色（把插入的节点设为红色，如果导致路径上有连续两个红色节点存在，就需要执行3）
3.修正（多次旋转与重新着色之后使插入后的树重新成为红黑树）
《算法导论》中插入操作的伪代码如下：
插入操作的伪代码：
RB-INSERT(T, z)
y ← nil[T] // 新建节点“y”，将y设为空节点。
x ← root[T] // 设“红黑树T”的根节点为“x”
while x ≠ nil[T] // 找出要插入的节点“z”在二叉树T中的位置“y”
do y ← x
if key[z] < key[x]
then x ← left[x]
else x ← right[x]
p[z] ← y // 设置 “z的父亲” 为 “y”
if y = nil[T]
then root[T] ← z // 情况1：若y是空节点，则将z设为根
else if key[z] < key[y]
then left[y] ← z // 情况2：若“z所包含的值” < “y所包含的值”，则将z设为“y的左孩子”
else right[y] ← z // 情况3：(“z所包含的值” >= “y所包含的值”)将z设为“y的右孩子”
left[z] ← nil[T] // z的左孩子设为空
right[z] ← nil[T] // z的右孩子设为空。至此，已经完成将“节点z插入到二叉树”中了。
color[z] ← RED // 将z着色为“红色”
RB-INSERT-FIXUP(T, z) // 通过RB-INSERT-FIXUP对红黑树的节点进行颜色修改以及旋转，让树T仍然是一颗红黑树
《算法导论》中插入后修正操作的伪代码如下：
修正操作的伪代码：
RB-INSERT-FIXUP(T, z)
while color[p[z]] = RED // 若“当前节点(z)的父节点是红色”，这时就产生两个连着的红色节点了，则进行以下处理。
do if p[z] = left[p[p[z]]] // 若“z的父节点”是“z的祖父节点的左孩子”，则进行以下处理。
then y ← right[p[p[z]]] // 将y设置为“z的叔叔节点(z的祖父节点的右孩子)”
if color[y] = RED // Case 1条件：叔叔是红色
then color[p[z]] ← BLACK ▹ Case 1 // (01) 将“父节点”设为黑色。
color[y] ← BLACK ▹ Case 1 // (02) 将“叔叔节点”设为黑色。
color[p[p[z]]] ← RED ▹ Case 1 // (03) 将“祖父节点”设为“红色”。
z ← p[p[z]] ▹ Case 1 // (04) 将“祖父节点”设为“当前节点”(红色节点)
else if z = right[p[z]] // Case 2条件：叔叔是黑色，且当前节点是右孩子
then z ← p[z] ▹ Case 2 // (01) 将“父节点”作为“新的当前节点”。
LEFT-ROTATE(T, z) ▹ Case 2 // (02) 以“新的当前节点”为支点进行左旋。
// Case 3条件：叔叔是黑色，且当前节点是左孩子。
color[p[z]] ← BLACK ▹ Case 3 // (01) 将“父节点”设为“黑色”。
color[p[p[z]]] ← RED ▹ Case 3 // (02) 将“祖父节点”设为“红色”。
RIGHT-ROTATE(T, p[p[z]]) ▹ Case 3 // (03) 以“祖父节点”为支点进行右旋。
else (same as then clause with "right" and "left" exchanged) // 若“z的父节点”是“z的祖父节点的右孩子”，将上面的操作中“right”和“left”交换位置，然后依次执行。
color[root[T]] ← BLACK插入修正的三种情况：
1.父节点是红色，叔节点是红色
方法：将父节点和叔叔节点涂黑，祖父结点涂红，把当前节点指向祖父节点
2.父节点是红色，叔节点是黑色，插入节点是右孩子
方法：以父节点为支点左旋
3.父节点是红色，叔节点是黑色，插入节点是左孩子
方法：父节点变为黑色，祖父节点变为红色，以祖父节点为支点右旋
四：红黑树的删除
步骤：
1.删除节点（二叉搜索树的删除操作，如果删除的是黑色节点，则可能导致红黑树性质改变，就需要执行2）
2.修正（多次旋转与重新着色之后使插入后的树重新成为红黑树）
《算法导论》中删除操作的伪代码如下：
删除操作的伪代码
RB-DELETE(T, z)
if left[z] = nil[T] or right[z] = nil[T]
then y ← z // 若“z的左孩子” 或 “z的右孩子”为空，则将“z”赋值给 “y”；
else y ← TREE-SUCCESSOR(z) // 否则，将“z的后继节点”赋值给 “y”。
if left[y] ≠ nil[T]
then x ← left[y] // 若“y的左孩子” 不为空，则将“y的左孩子” 赋值给 “x”；
else x ← right[y] // 否则，“y的右孩子” 赋值给 “x”。
p[x] ← p[y] // 将“y的父节点” 设置为 “x的父节点”
if p[y] = nil[T]
then root[T] ← x // 情况1：若“y的父节点” 为空，则设置“x” 为 “根节点”。
else if y = left[p[y]]
then left[p[y]] ← x // 情况2：若“y是它父节点的左孩子”，则设置“x” 为 “y的父节点的左孩子”
else right[p[y]] ← x // 情况3：若“y是它父节点的右孩子”，则设置“x” 为 “y的父节点的右孩子”
if y ≠ z
then key[z] ← key[y] // 若“y的值” 赋值给 “z”。注意：这里只拷贝z的值给y，而没有拷贝z的颜色！！！
copy y's satellite data into z
if color[y] = BLACK
then RB-DELETE-FIXUP(T, x) // 若“y为黑节点”，则调用
return y 《算法导论》中删除后修正操作的伪代码如下：
删除后修正操作伪代码：
RB-DELETE-FIXUP(T, x)
while x ≠ root[T] and color[x] = BLACK
do if x = left[p[x]]
then w ← right[p[x]] // 若 “x”是“它父节点的左孩子”，则设置 “w”为“x的兄弟”(即w为x父节点的右孩子)
if color[w] = RED // Case 1: x是“黑+黑”节点，x的兄弟节点是红色。(此时x的父节点和x的兄弟节点的子节点都是黑节点)。
then color[w] ← BLACK ▹ Case 1 // (01) 将x的兄弟节点设为“黑色”。
color[p[x]] ← RED ▹ Case 1 // (02) 将x的父节点设为“红色”。
LEFT-ROTATE(T, p[x]) ▹ Case 1 // (03) 对x的父节点进行左旋。
w ← right[p[x]] ▹ Case 1 // (04) 左旋后，重新设置x的兄弟节点。
if color[left[w]] = BLACK and color[right[w]] = BLACK // Case 2: x是“黑+黑”节点，x的兄弟节点是黑色，x的兄弟节点的两个孩子都是黑色。
then color[w] ← RED ▹ Case 2 // (01) 将x的兄弟节点设为“红色”。
x ← p[x] ▹ Case 2 // (02) 设置“x的父节点”为“新的x节点”。
else if color[right[w]] = BLACK // Case 3: x是“黑+黑”节点，x的兄弟节点是黑色；x的兄弟节点的左孩子是红色，右孩子是黑色的。
then color[left[w]] ← BLACK ▹ Case 3 // (01) 将x兄弟节点的左孩子设为“黑色”。
color[w] ← RED ▹ Case 3 // (02) 将x兄弟节点设为“红色”。
RIGHT-ROTATE(T, w) ▹ Case 3 // (03) 对x的兄弟节点进行右旋。
w ← right[p[x]] ▹ Case 3 // (04) 右旋后，重新设置x的兄弟节点。
color[w] ← color[p[x]] ▹ Case 4 // Case 4: x是“黑+黑”节点，x的兄弟节点是黑色；x的兄弟节点的右孩子是红色的。(01) 将x父节点颜色 赋值给 x的兄弟节点。
color[p[x]] ← BLACK ▹ Case 4 // (02) 将x父节点设为“黑色”。
color[right[w]] ← BLACK ▹ Case 4 // (03) 将x兄弟节点的右子节设为“黑色”。
LEFT-ROTATE(T, p[x]) ▹ Case 4 // (04) 对x的父节点进行左旋。
x ← root[T] ▹ Case 4 // (05) 设置“x”为“根节点”。
else (same as then clause with "right" and "left" exchanged) // 若 “x”是“它父节点的右孩子”，将上面的操作中“right”和“left”交换位置，然后依次执行。
color[x] ← BLACK 删除的节点是黑色的时候才可能导致原红黑树的性质出问题。
根据二叉搜索树的删除操作，节点被删除后总有一个节点来顶替它，将顶替的节点设为当前节点。当前节点会继承被删除节点的黑色，也就是说，当前节点的颜色是：黑+黑或者红+黑。
如果当前节点是红+黑，那么直接将当前节点染黑，红黑树的性质就恢复。
如果当前节点是黑+黑，并且当前节点是根节点，那么什么都不做，红黑树的性质就恢复。
剩下的四种情况（当前节点是：黑+黑，并且不是根节点）：
1.兄弟是红（父节点为黑，兄弟节点的子节点全是黑）
方法：父变红，兄弟节点染黑，以父节点左旋，注意这时候的兄弟节点应是原来兄弟节点的子节点
2.兄弟是黑，兄弟的两个子节点全是黑
方法：把当前节点和兄弟节点中抽取一重黑色追加到父节点上，把父节点当成新的当前节点，重新进入算法。
3.兄弟是黑，左子是红，右子是黑
方法：把兄弟结点染红，兄弟左子节点染黑，之后再在兄弟节点为支点右旋，之后重新进入算法。此是把当前的情况转化为情况4
4.兄弟是黑，右子是红，左子任意
方法：兄弟变红，父变黑，兄弟右子变黑，以父节点为支点左旋，此时算法结束，红黑树所有性质调整正确，
扫一扫
5495
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
