当我们用单个模型(比如决策树、逻辑回归)做预测时,很容易出现 “过拟合”(比如决策树长得太复杂,只适应训练数据)或 “欠拟合”(比如模型太简单,抓不住数据规律)。而集成算法的思路很简单 ——“三个臭皮匠顶个诸葛亮”:通过组合多个 “弱模型”(预测效果一般的模型),形成一个 “强模型”(预测更准确、更稳定的模型)。今天我们就从最经典的集成算法(Bagging、Boosting、Stacking)入手,用代码实现并可视化结果,帮你彻底搞懂它的工作逻辑。
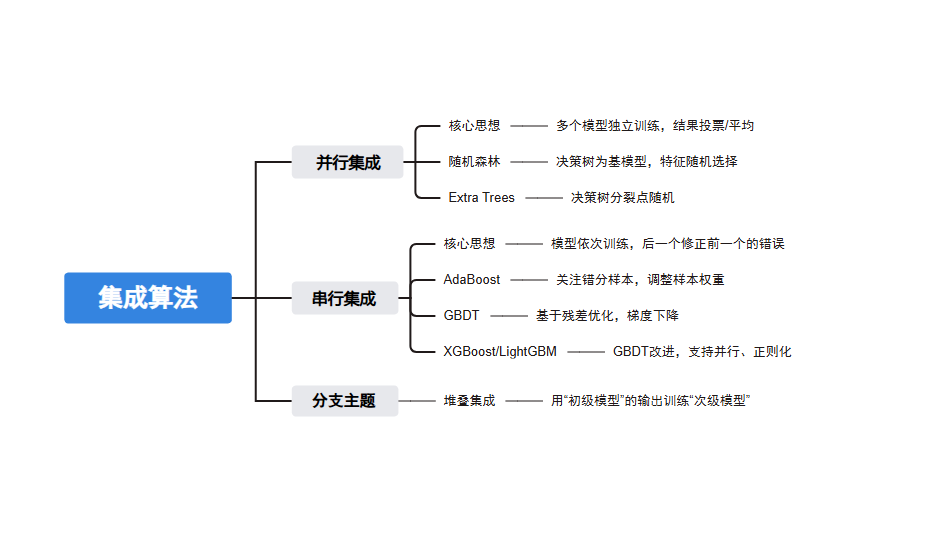
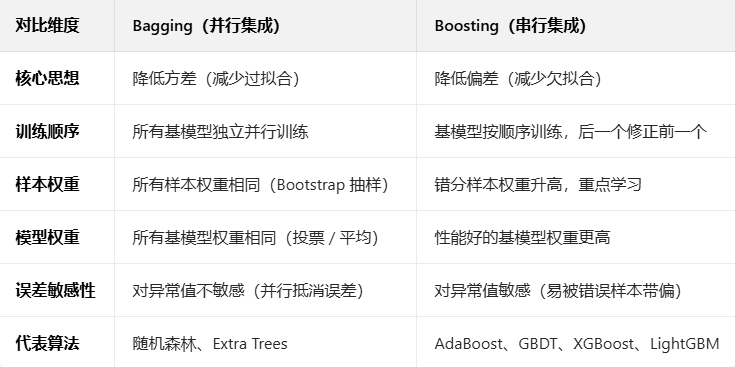
通俗解释来说:
- Bagging 像 “一群独立的裁判同时打分,最后取平均”,重点是 “避免单个裁判的极端偏见”(降低方差);
- Boosting 像 “一个裁判先打分,后面的裁判专门修正前一个的错误”,重点是 “逐步减少错误”(降低偏差),但如果前一个裁判错得离谱(异常值),后面的也容易跟着错。
- 堆叠集成在实际中并不常用。
下面以随机森林(Random Forest)为例,为大家详细展开其核心原理和应用场景:
一. 随机森林 = 多棵 “随机” 的决策树一起投票
-
怎么 “随机”?
- 样本随机:从训练集中随机选一部分数据(有放回,即 Bootstrap 抽样),给每棵树用;
- 特征随机:每棵树分裂时,只从所有特征中随机选一部分(比如总特征数的√n),避免单一强特征主导。
-
怎么 “投票”?
- 分类问题:多棵树预测的类别中,出现次数最多的就是最终结果(硬投票);
- 回归问题:多棵树预测结果的平均值就是最终结果。
-
为什么有效?
- 单棵决策树容易 “过拟合”(比如只看 “年龄” 就判断是否违约),但多棵随机树的 “错误” 会相互抵消,结果更稳定。
二. 算法原理
随机森林是一种集成学习方法,通过构建多个决策树(Decision Tree)并综合它们的预测结果 来提高模型准确性和鲁棒性。其核心特点包括:
- Bootstrap采样(有放回抽样):每棵树的训练数据从原始数据集中随机抽取,允许重复样本。
- 特征随机性:每棵树在分裂节点时,仅从随机子集中选择最优特征(而非全部特征),增强多样性。
示例:
假设数据集有1000个样本和20个特征,随机森林可能:
- 为每棵树抽取800个样本(可重复),并随机选择5个特征用于节点分裂。
三. 关键步骤
- 构建多棵决策树:
- 通过Bootstrap采样生成N个差异化的训练子集。
- 每棵树独立训练,过程中限制特征选择范围(如
max_features=sqrt(n_features))。
- 投票或平均:
- 分类任务:最终结果由多数投票决定。
- 回归任务:输出所有树预测值的平均值。
四. 代码实现(以 “随机森林分类(鸢尾花数据集)” 为例)
1. 代码结构
pip install scikit-learn
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris # 自带数据集
from sklearn.ensemble import RandomForestClassifier # 随机森林
from sklearn.model_selection import train_test_split # 划分训练/测试集
from sklearn.metrics import accuracy_score, confusion_matrix # 评估指标
from sklearn.tree import plot_tree # 可视化单棵决策树
# 2. 加载并预处理数据
iris = load_iris() # 加载鸢尾花数据集(分类任务:3种花卉,4个特征)
X = iris.data # 特征:花萼长度、花萼宽度、花瓣长度、花瓣宽度
y = iris.target # 标签:0/1/2(对应3种花卉)
feature_names = iris.feature_names # 特征名(用于后续可视化)
target_names = iris.target_names # 标签名
# 划分训练集(80%)和测试集(20%)
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=42 # random_state固定随机种子,确保结果可复现
)
# 3. 训练随机森林模型
rf_model = RandomForestClassifier(
n_estimators=100, # 决策树数量:100棵
max_depth=3, # 每棵树最大深度:避免过拟合
random_state=42
)
rf_model.fit(X_train, y_train) # 用训练集训练模型
# 4. 模型预测与评估
y_pred = rf_model.predict(X_test) # 用测试集预测
accuracy = accuracy_score(y_test, y_pred) # 计算准确率
conf_matrix = confusion_matrix(y_test, y_pred) # 计算混淆矩阵
# 打印结果
print(f"随机森林测试集准确率:{accuracy:.2f}") # 输出:准确率约0.97(很高)
print("混淆矩阵:")
print(conf_matrix)
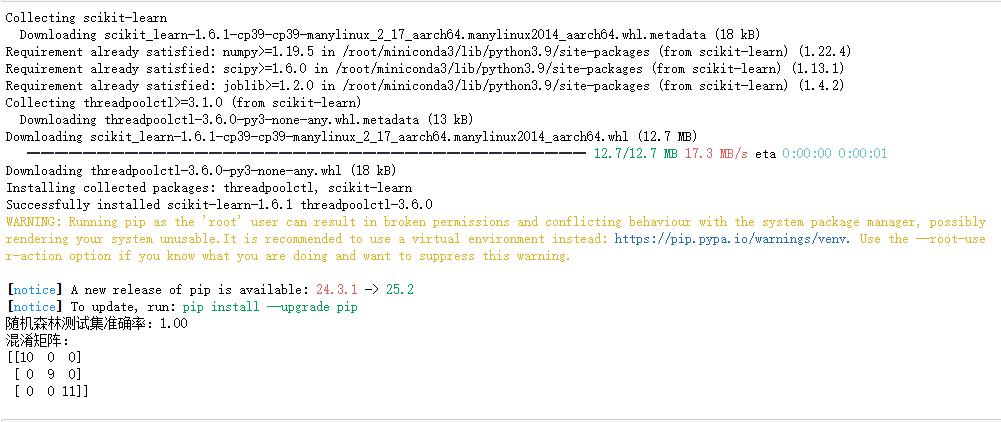
2.图片可视化
# 可视化随机森林中的第一棵决策树
plt.figure(figsize=(12, 8)) # 设置图的大小
plot_tree(
rf_model.estimators_[0], # 取第1棵树
feature_names=feature_names, # 特征名
class_names=target_names, # 类别名
filled=True, # 用颜色填充节点
rounded=True # 节点圆角
)
plt.title("随机森林中的单棵决策树", fontsize=15)
plt.savefig("random_forest_tree.png", dpi=300, bbox_inches="tight") # 保存图片
plt.show()
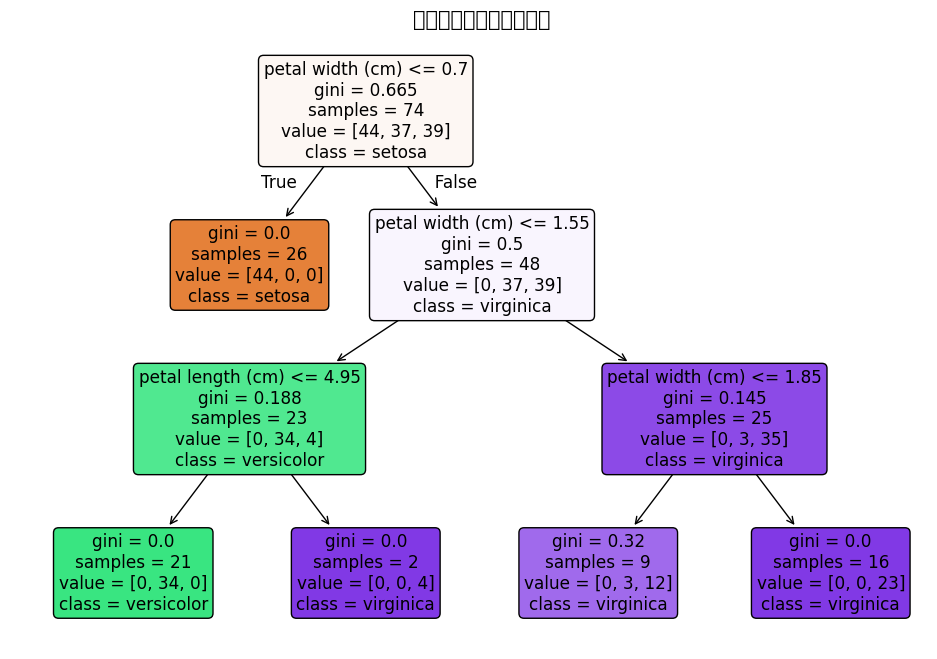
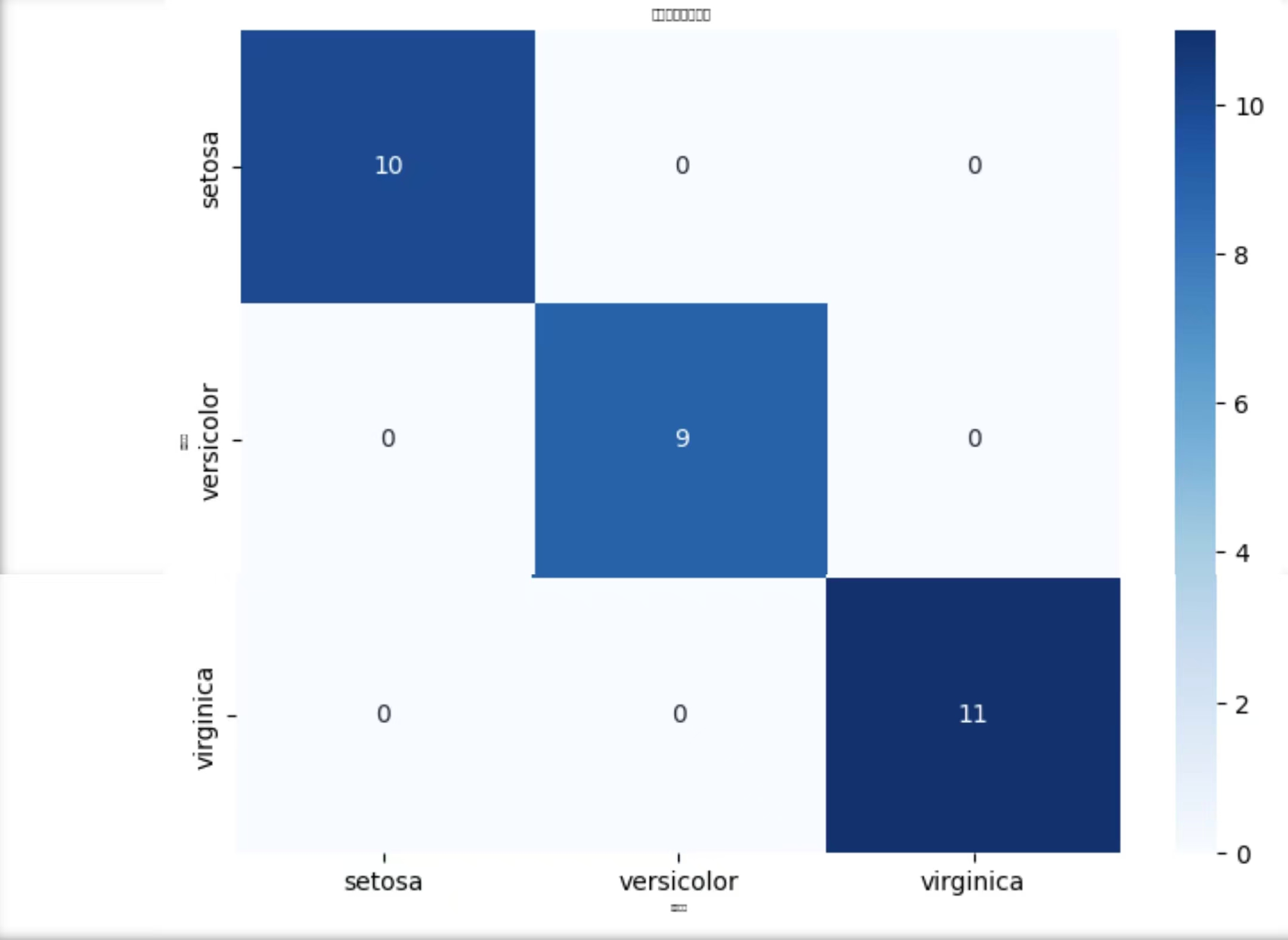
3. 混淆矩阵热力图(展示预测效果)
pip install seaborn
import seaborn as sns
# 绘制混淆矩阵热力图
plt.figure(figsize=(8, 6))
sns.heatmap(
conf_matrix, # 混淆矩阵数据
annot=True, # 显示数值
fmt="d", # 数值格式(整数)
cmap="Blues", # 颜色映射
xticklabels=target_names, # x轴:预测类别
yticklabels=target_names # y轴:真实类别
)
plt.xlabel("预测类别", fontsize=3)
plt.ylabel("真实类别", fontsize=3)
plt.title("随机森林混淆矩阵", fontsize=5)
plt.savefig("confusion_matrix.png", dpi=50, bbox_inches="tight")
plt.show()
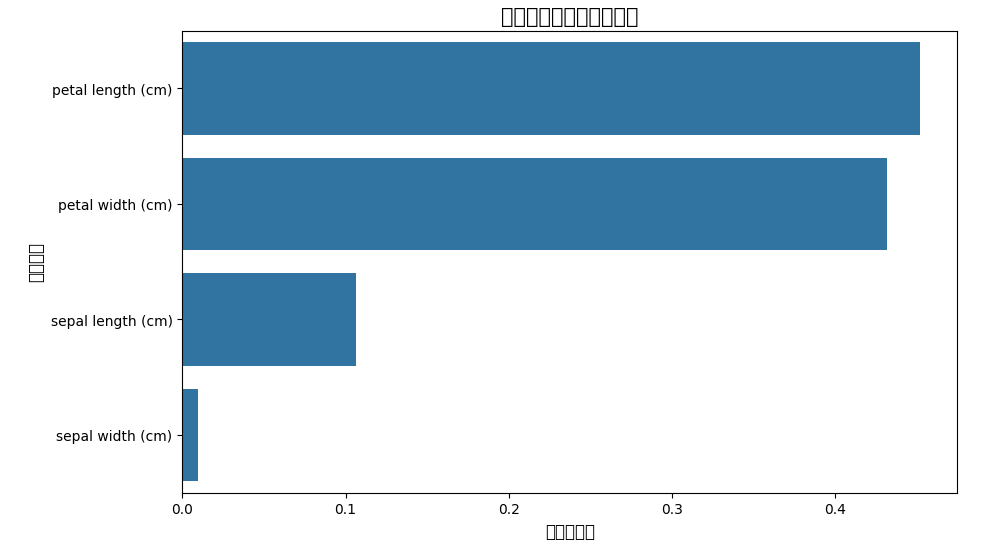
4. 特征重要性图
# 计算特征重要性
feature_importance = rf_model.feature_importances_
# 对特征名和重要性排序(从大到小)
sorted_idx = np.argsort(feature_importance)[::-1]
sorted_feature_names = [feature_names[i] for i in sorted_idx]
sorted_importance = feature_importance[sorted_idx]
# 绘制特征重要性柱状图
plt.figure(figsize=(10, 6))
sns.barplot(x=sorted_importance, y=sorted_feature_names)
plt.xlabel("特征重要性", fontsize=12)
plt.ylabel("特征名称", fontsize=12)
plt.title("随机森林特征重要性排序", fontsize=15)
plt.savefig("feature_importance.png", dpi=300, bbox_inches="tight")
plt.show()
总结
1. 核心知识点回顾
- 随机森林是Bagging 思想的代表,通过 “样本随机 + 特征随机” 生成多棵决策树,最终用 “投票 / 平均” 输出结果;
- 优势:抗过拟合能力强、对异常值不敏感、能输出特征重要性;
- 劣势:训练速度比单棵决策树慢(需训练多棵树)、对小样本数据集效果可能不如简单模型(如逻辑回归)。
2. 典型应用:
- 金融风控(信用评分)
- 医疗诊断(疾病预测)
- 图像分类(特征重要性分析)
3. 参数调优建议
n_estimators:树的数量(通常100-500)。max_depth:默认 None,建议设为 3-10(太深易过拟合,太浅易欠拟合)。max_features(每棵树用的特征数):分类任务默认√n,回归任务默认 n/3(可按特征数量调整)。





















 21
21










