目录
1 前言
鲁棒优化是电力系统研究的热点,而两阶段鲁棒和分布鲁棒研究就成为各类期刊(sci/ei/核心)的宠儿,最简单的思路是通过改变模型(考虑设备备用等)和组合创新(需求响应等),得到该类问题另外一个方向的深入研究结论。这里仅仅为发文章提供一点点参考建议和思路!
本次和大家分享的是33节点系统的两阶段鲁棒优化调度程序,该程序主要是复现《两阶段鲁棒优化的主动配电网动态无功优化》-熊壮壮,具体文章内容可自行下载了解,在这里主要对模型部分和配网两阶段鲁棒计算步骤进行分析。
2基本内容
2.1 配网两阶段鲁棒模型
以网损为目标,包括功率平衡、网络潮流、电压电流、蓄电池出力以及无功设备出力等约束,具体模型如下:
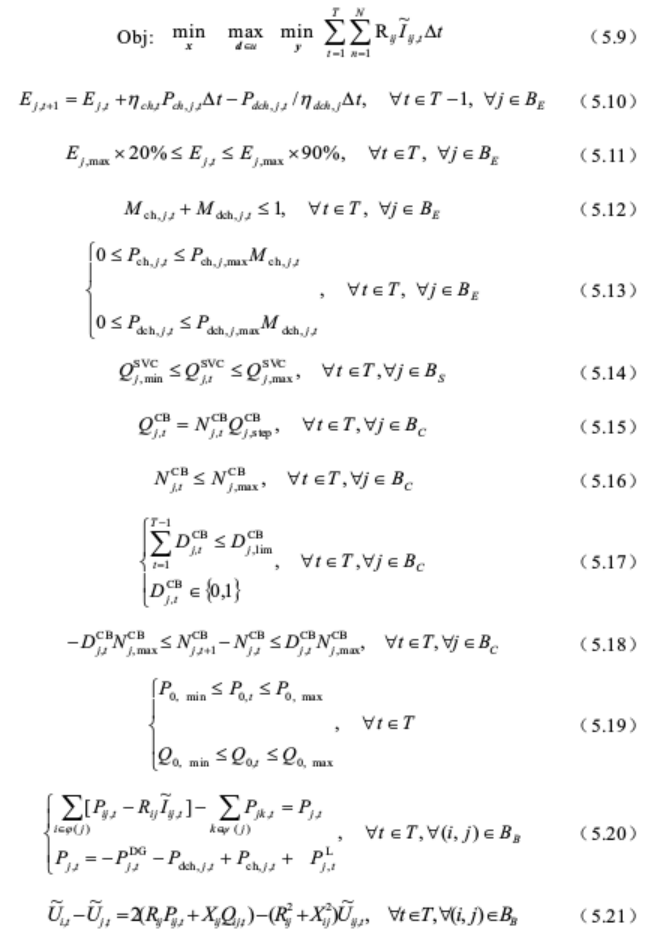
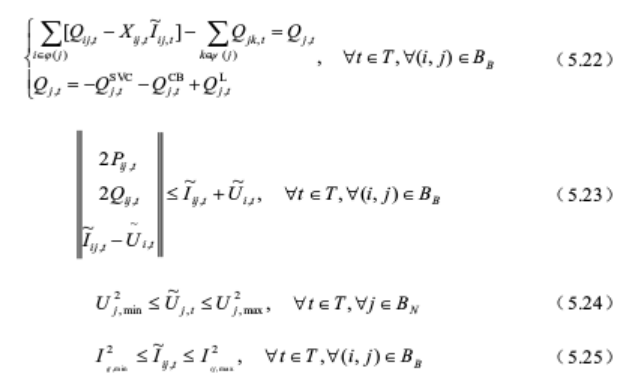
模型中一个难题是潮流模型凸化处理,原二阶锥约束如下:
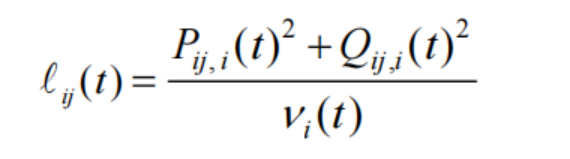
对锥松弛凸化,得到:
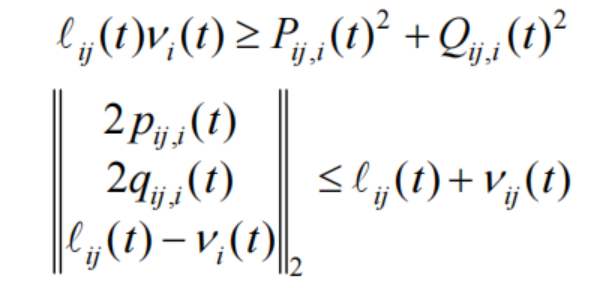
经过紧凑形式转化和推导,得到主问题和子问题形式如下:
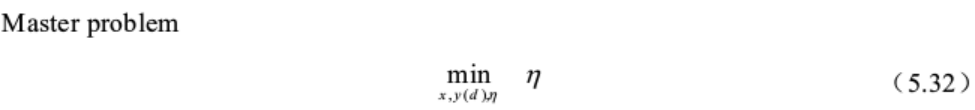

2.2 求解步骤

3部分程序
本程序编程过程中最大的难题是采用三维变量形式,变量维度包括数量、时间和迭代次数三个维度,采用yalmip三维变量形式求解速度要略慢一些,之前程序6节点电网两阶段鲁棒优化调度matlab采用将三维变量转化为二维变量形式,运行效率就比较高。
主程序部分代码
for km=1:kn
yalmip('clear');
SP;%通过上面的初始值数据运行子问题
u_sp(1,:,km)=wind_sp1;%更新不确定性变量
u_sp(2,:,km)=wind_sp2;
u_sp(3,:,km)=wind_sp3;
u_sp(4,:,km)=pv_sp1;
u_sp(5,:,km)=pv_sp1;%更新不确定性变量
UB1=min(UB,UB1);%更新CCG算法中的UB
UBc(km)=UB1;
test;%运行主问题
LB1=max(LB,LB1);%更新CCG算法中的LB
LBc(km)=LB1;
p(km)=UB1-LB1;%判断收敛性
end
主问题部分程序
%% 通用约束
for j=1:km
C = [C, Vmin <= V(:,:,j),V(:,:,j) <= Vmax];%电压约束
C = [C, Pgmin <= Pg(:,:,j),Pg(:,:,j) <= Pgmax,Qgmin <= Qg(:,:,j),Qg(:,:,j) <= Qgmax];
end
C = [C, 0 <= I,I <= 6];
for j=1:km
C = [C, alfa>=sum(sum(I(:,:,j).*(r*ones(1,T))))];
end
%% 4.设目标函数
f = alfa;%网损最小
4程序结果
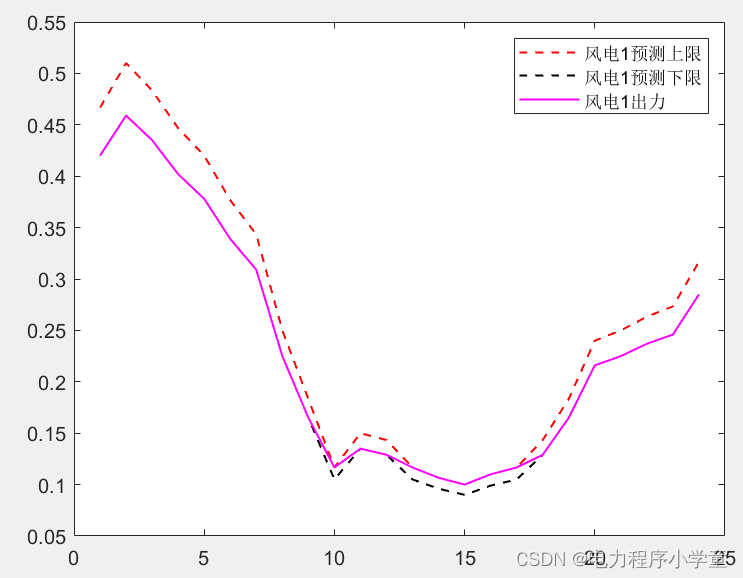
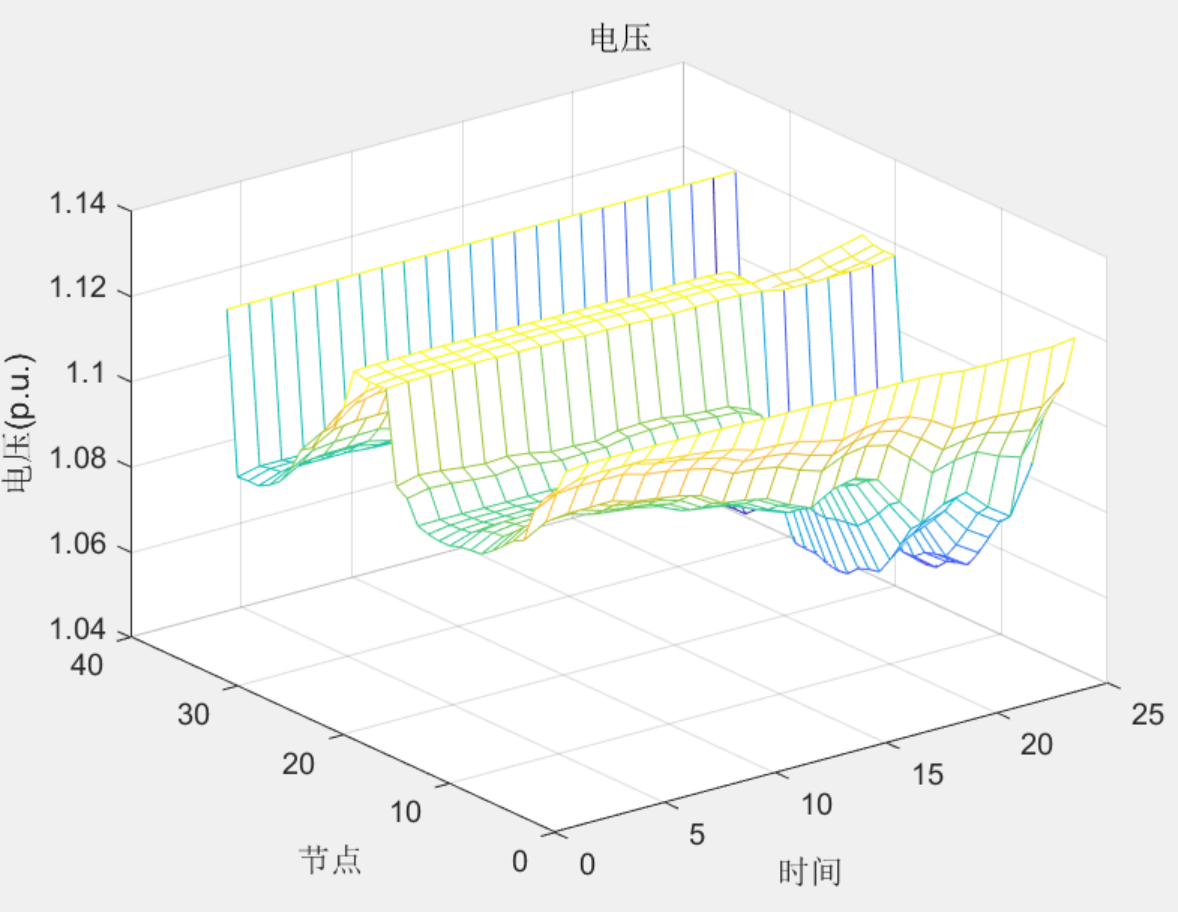
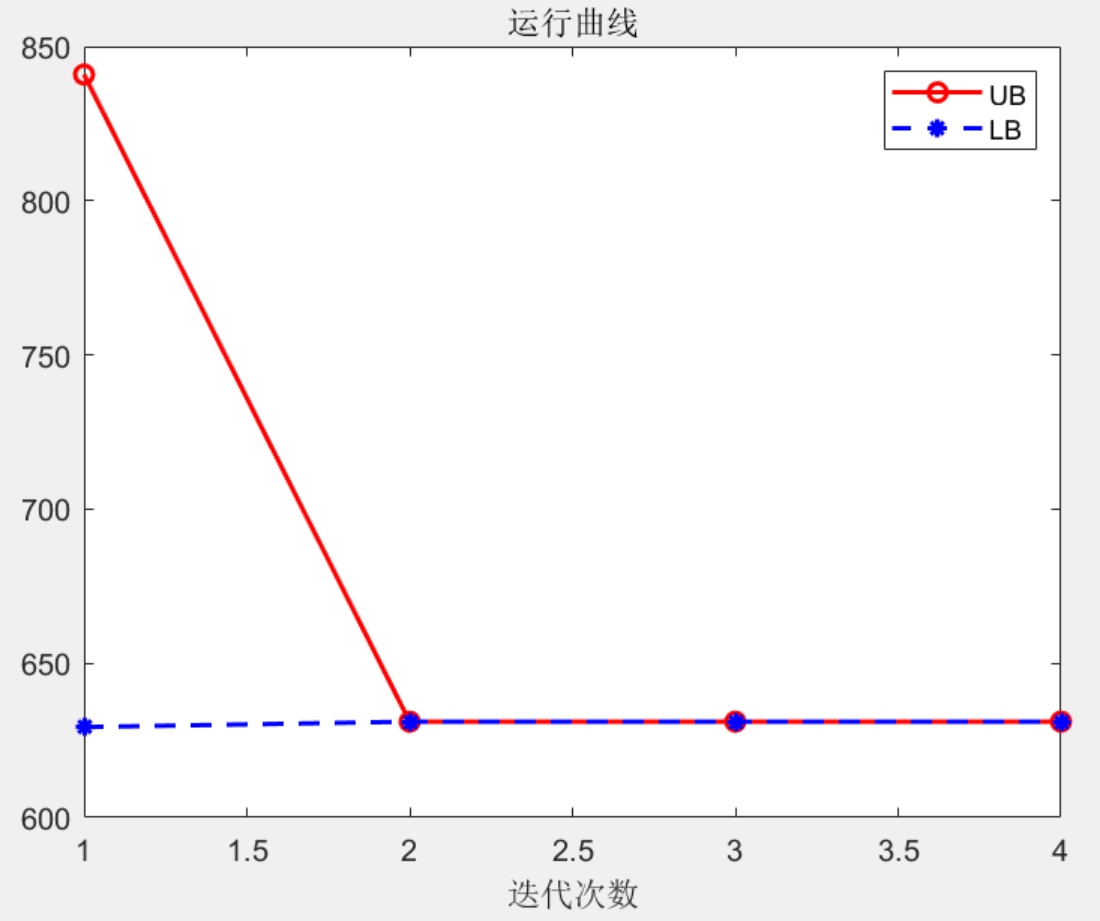
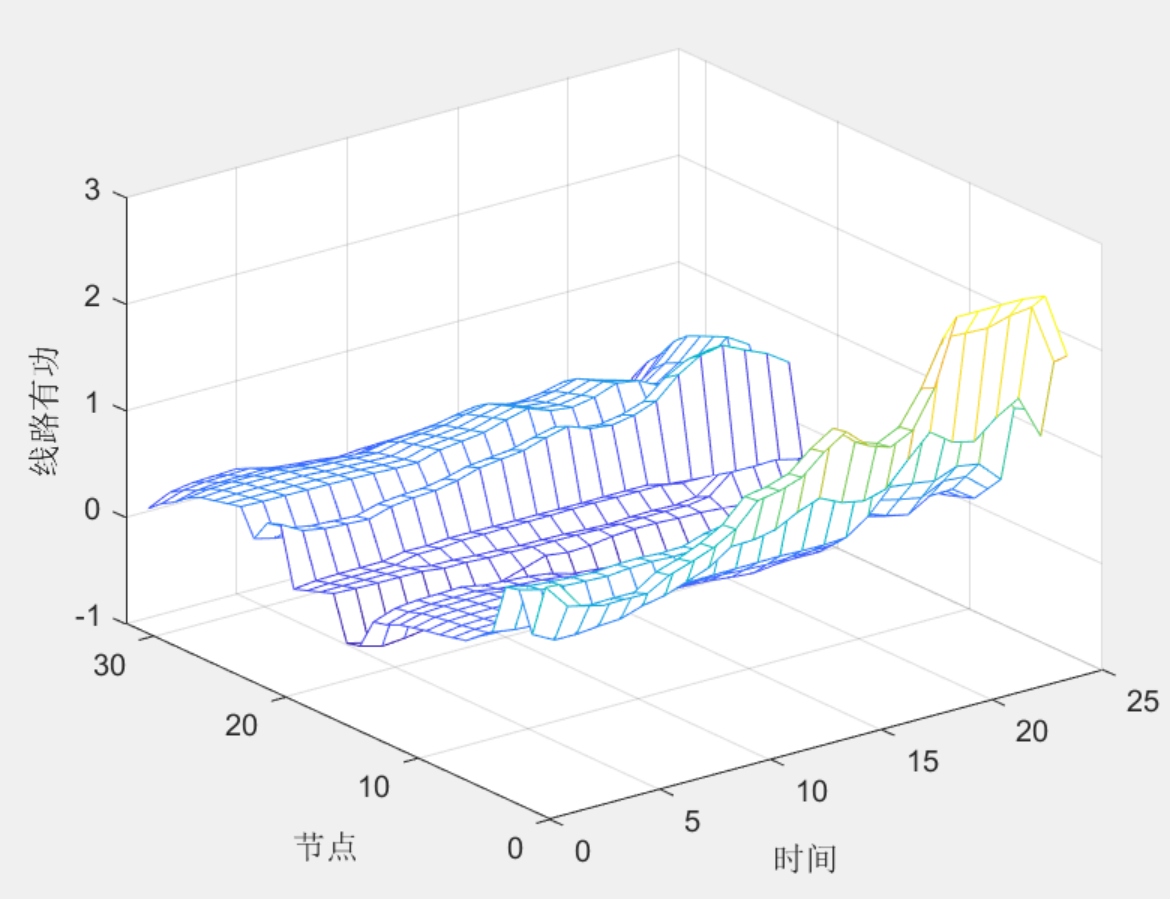
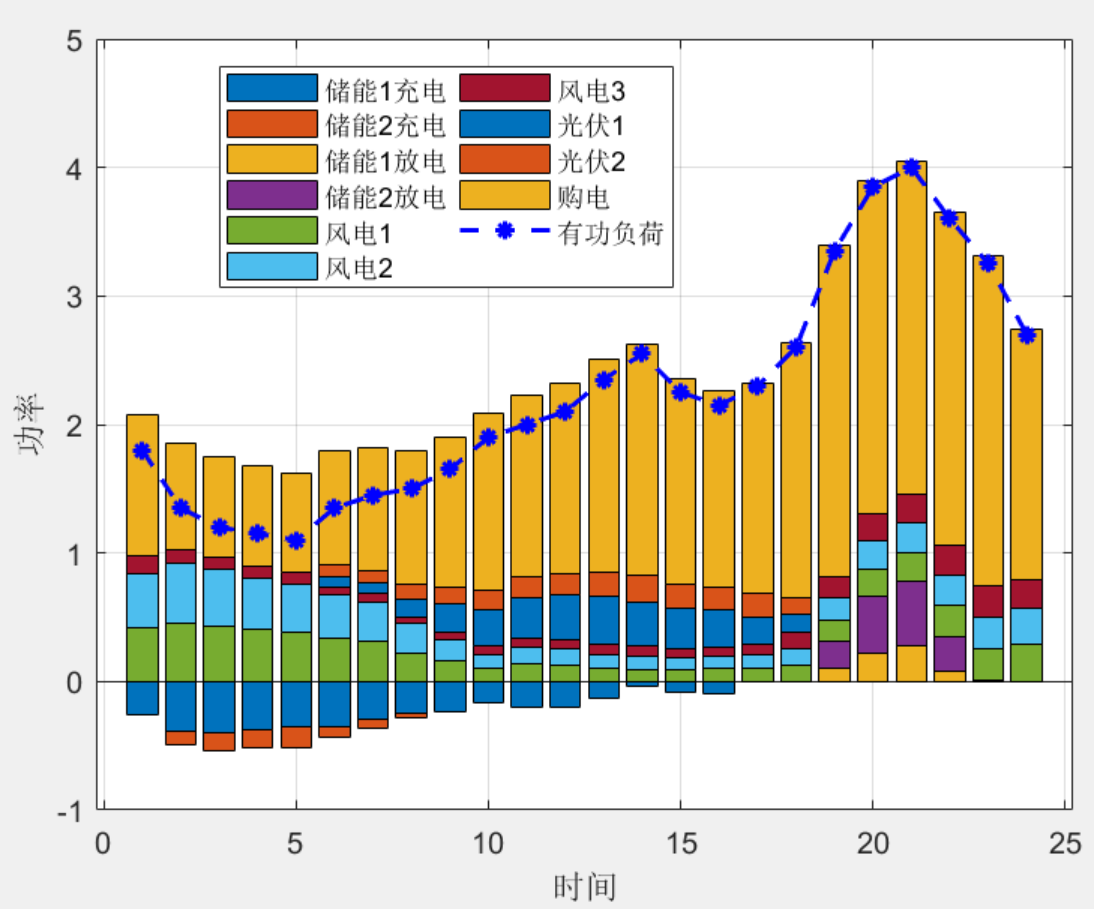







 本文介绍了一个用于33节点系统的两阶段鲁棒优化调度程序,基于《两阶段鲁棒优化的主动配电网动态无功优化》的研究,重点讨论了配网两阶段鲁棒模型的构建,包括网损最小化目标和潮流模型的凸化处理。文章还阐述了求解步骤及程序实现中的难点,如三维变量处理和优化效率问题。
本文介绍了一个用于33节点系统的两阶段鲁棒优化调度程序,基于《两阶段鲁棒优化的主动配电网动态无功优化》的研究,重点讨论了配网两阶段鲁棒模型的构建,包括网损最小化目标和潮流模型的凸化处理。文章还阐述了求解步骤及程序实现中的难点,如三维变量处理和优化效率问题。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










