本文介绍了平衡二叉树（AVL树）的概念及其性质，并通过具体实例解释了如何确定在一个包含特定数量节点的平衡二叉树中进行查找的最大比较次数。
平衡二叉树又称AVL树，它或者是一棵空树，或者是具有下列性质的二叉树：它的左子树和右子树都是平衡二叉树，
且左子树和右子树的深度之差的绝对值不超过1，若将二叉树上节点的平衡因子BF定义为该节点的左子树的深度减去它的右子树的深度，
则平衡二叉树上所有节点的平衡因子只可能是-1、0和1。
只要二叉树上有一个节点的平衡因子的绝对值大于1，则该二叉树不平衡。AVL树上任何节点的左右子树的深度之差都不超过1
则可以证明它的深度和log2n是同数量级的(n为节点个数)。
因此，它的平均查找长度也和log2n同数量级。
但是这个问题是针对于平均查找长度，而不是最多的查找次数：
问题具体的例子：
比如含有12个结点的平衡二叉树中查找某一个结点最多的比较次数？
这个因为问到的是具体的12个结点的平衡二叉树，此时是一个确切的问题了
可以画出这个结点数为12的平衡二叉树的图
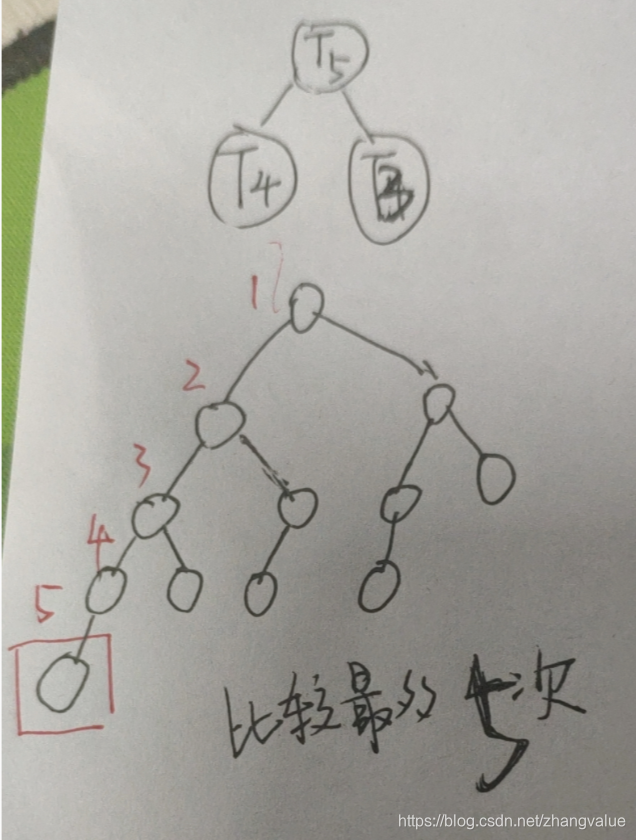
如上图所示，比较的最多肯定是要到深度最大的结点上了，最终比较次数就是5次了，而不是 log2N<4了
扫一扫
999
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
