在证明关于梯度算法等一系列算法的时候,我们总会得到类似如下情形的结果
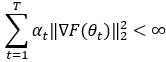
对于α_t,我们通常设置为1/t或1/√t,有时也会这设置α_t使其满足
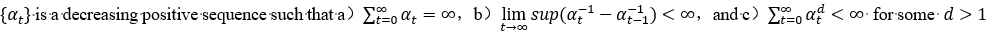
但我们并不能直接通过α_t发散来得到梯度范数收敛
下面我们给出反例:
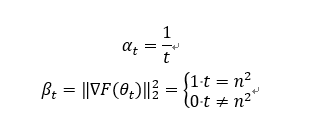
故我们无法直接得到梯度收敛的结论
关于证明算法收敛时使用min||g_t||的原因
最新推荐文章于 2025-04-08 16:23:43 发布
在证明关于梯度算法等一系列算法的时候,我们总会得到类似如下情形的结果
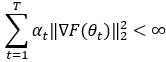
对于α_t,我们通常设置为1/t或1/√t,有时也会这设置α_t使其满足
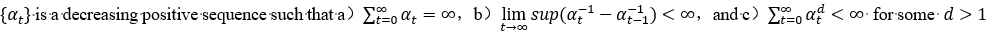
但我们并不能直接通过α_t发散来得到梯度范数收敛
下面我们给出反例:
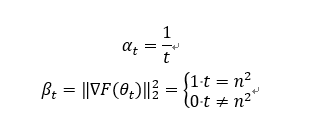
故我们无法直接得到梯度收敛的结论
 6122
6122
 1534
1534
 3220
3220
 4830
4830

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


