数据结构之图的最小生成树

最新推荐文章于 2022-04-27 01:15:39 发布

Joeyos

最新推荐文章于 2022-04-27 01:15:39 发布

阅读量331

点赞数 1

分类专栏：数据结构

本文链接：https://blog.youkuaiyun.com/zhangquan2015/article/details/82843575

版权

本文介绍了图的最小生成树的概念，重点讲解了两种经典算法：普里姆算法和克鲁斯卡尔算法。通过详细步骤解析了普里姆算法如何从顶点出发构建最小生成树，以及克鲁斯卡尔算法如何直接寻找最小权值的边来构建生成树，同时避免形成环路。最后展示了两种算法的运行结果。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

我们把构造连通网的最小代价生成树称为最小生成树，找连通网的最小生成树，经典的有两种算法：普里姆算法（Prim）和克鲁斯卡尔算法（Kruskal）。

普里姆算法

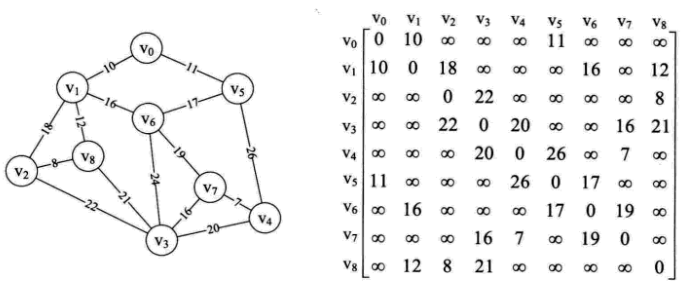
有如下邻接矩阵，9个顶点，左侧数字为行号，INFINITY为极大值65535，MAXVEX为顶点个数最大值，此处大于等于9即可。
在这里插入图片描述

void MiniSpanTree_Prim(MGraph G)/* Prim算法生成最小生成树  */
{
   
	int min, i, j, k;
	int adjvex[MAXVEX];		/* 保存相关顶点下标 */
	int lowcost[MAXVEX];	/* 保存相关顶点间边的权值 */
	lowcost[0] = 0;/* 初始化第一个权值为0，即v0加入生成树。lowcost的值为0，在这里就是此下标的顶点已经加入生成树 */
	adjvex[0] = 0;			/* 初始化第一个顶点下标为0 */
	for(i = 1; i < G.numVertexes; i++)	/* 循环除下标为0外的全部顶点 */
	{
   
		lowcost[i] = G.arc[0][i];	/* 将v0顶点与之有边的权值存入数组 */
		adjvex[i] = 0;					/* 初始化都为v0的下标 */
	}
	for(i = 1; i < G.numVertexes; i++)
	{
   
		min = INFINITY;	/* 初始化最小权值为∞，通常设置为不可能的大数字如32767、65535等 */
		j = 1;k = 0;
		while(j < G.numVertexes)	/* 循环全部顶点 */
		{
   
			if(lowcost[j]!=0 && lowcost[j] < min)/* 如果权值不为0且权值小于min */
			{
   	
				min = lowcost[j];	/* 则让当前权值成为最小值 */
				k = j;			/* 将当前最小值的下标存入k */
			}
			j++;
		}
		printf("(%d, %d)\n", adjvex[k], k);/* 打印当前顶点边中权值最小的边 */
		lowcost[k] = 0;/* 将当前顶点的权值设置为0,表示此顶点已经完成任务 */
		for(j = 1; j < G.numVertexes; j++)	/* 循环所有顶点 */
		{
   
			if(lowcost[j]!=0 && G.arc[k][j] < lowcost[j]) 
			{
   /* 如果下标为k顶点各边权值小于此前这些顶点未被加入生成树权值 */
				lowcost[j] = G.arc[k][j];/* 将较小的权值存入lowcost相应位置 */
				adjvex[j] = k;				/* 将下标为k的顶点存入adjvex */
			}
		}
	}
}

创建两个一维数组lowcost和adjvex，长度都为顶点个数9。
第6-7行我们分别给这两个数组的第一个下标位赋值为0，arjvex[0]=0 。意思是从顶点v0开始，lowcost[0]=0就表示v0已经被纳入到最小生成树中，之后凡是lowcost数组中的值被设置为0就是表示此下标的顶点被纳入最小生成树。
第8-12行表示我们读取邻接矩阵的第一行数据。将数值赋值给lowcost数组，所以此时lowcost数组值为{0，10，65535，65535，65535，11，65535，65535，65535}，而arjvex则全部为0。此时，我们已经完成了整个初始化的工作，准备开始生成。
第13-36行，整个循环过程就是构造最小生成树的过程。
第15-16行，将min设置为一个极大值65535，它的目的是为了之后找到一定范围内的最小权值。j是用来做顶点下标循环的变量，k是用来存储最小权值的顶点下标。
第17-25行，循环中不断修改min为当前lowcost数组中最小值，并用k保留此最小值的顶点下标。经过循环后，min=10，k=1。lowcost[j]!=0表示已经是生成树的顶点不参与最小权值的查找。
第26行，因k=1，adjvex[1]=0，所以打印结果为（0,1），表示v0至v1边为最小生成树的第一条边。
第27行，此时因k=1，我们将lowcost[k]=0，就是说顶点v1纳入到最小生成树中，此时lowcost数组值为{0,0,65535,65535,65535,11,65535,65535,65535}。
第28-35行，j循环由1至8，因k=1，查找邻接矩阵的第v1行的各个权值，与lowcost的对应值比较，若更小则修改lowcost值，并将k值存入adjvex数组中。因第v1行有18,16,12均比65535小，所以最终lowcost为{0,0,18,65535,65535,11,16,65535,12}。adjvex数组的值为：{0,0,1,0,0,0,1,0,1}。第30行if判断的lowcost[j]!=0说明v0和v1已经是生成树的顶点，不参与最小权值的比对。
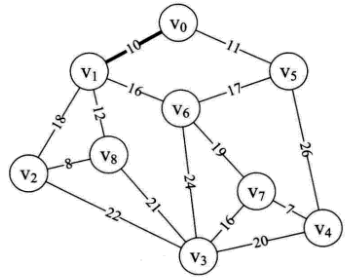
再次循环，第15行到第26行，此时min=11,k=5,adjvex[5]=0。因此打印结构为（0，5）。表示v0至v5边为最小生成树的第二条边：
接下来执行到第36行，lowcost数组的值为{0,0,18,65535,26,0,16,65535,12} ，adjvex数组的值为：{0,0,1,0,5,0,1,0,1}。
如此循环，最终得到生成树。

#include "stdio.h"    
#include "stdlib.h"   
#include "io.h"  
#include "math.h"  
#include "time.h"

#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0

#define MAXEDGE 20
#define MAXVEX 20
#define INFINITY 65535

typedef int Status;	/* Status是函数的类型,其值是函数结果状态代码，如OK等 */

typedef struct
{
   
	int arc[MAXVEX][MAXVEX];
	int numVertexes, numEdges;
}MGraph

最低0.47元/天解锁文章