基于FPGA的CIC滤波器设计（2）——以数字上下变频为例讲解

项目简述

我们上一篇博客对CIC滤波器的理论与实现进行了详细的介绍，相信同学们从前一篇博客可以进行相应的学习。但是CIC滤波器本质上就是 低通滤波器。为什么如此常用，只是因为CIC滤波器构成简单不需要乘法器，运行速度快，在通信中的上下变频中非常常用。当然CIC滤波器可是使用低通滤波器来实现，但是资源利用率不高。

本次项目我们将使用多级CIC滤波器进行抽取与插值操作，这样做的目的主要是为了提高阻带衰减，是有用信号的占比更大。但是提高阻带衰减的同时会降低通带衰减，这些特点也就决定了CIC滤波器在数字上下变频中的应用，因为该应用中信号的抽样频率远大于有用信号的频率。学习这一篇博客的时候一定要先学习上一篇博客，否则会导致概念不明白。

多级CIC滤波器

根据上一篇文章我们关于CIC滤波器严格的计算，可以发现单级CIC滤波器的第一旁瓣电平衰减固定为 13.46dB，且与滤波器的阶数无关。然而，这个 阻带衰减通常不满足实际中的要求，所以会把多个简单的CIC滤波器进行级联，所以称为 多级CIC滤波器。
不过增加CIC滤波器的级数也有不利的影响：通带衰减也随着增加。换句话说，对于给定的通带衰减要求，多 级CIC滤波器的通带范围会随着级数的增加而不断变窄，通带衰减也会随之增加。滤波器的设计不仅要考虑阻带误差容限，还要考虑通带误差容限，设计多级CIC滤波器时要注意考虑这个问题。这里再次强调CIC滤波器就是低通滤波器，至于为什么不使用其他的低通滤波器，而使用CIC滤波器，主要是因为结构简单。

其实，CIC滤波器大多应用于 抗混叠抽取/内插滤波器，也是因为上述的原因。因为在抗混叠应用中，有效信号频带往往远小于采样率，因此总可以设计出同时满足通带和阻带要求的CIC滤波器。

多级CIC滤波器的抽取操作

常见信号的抽取操作如下图：

从上面我们可以看出一般先进行抗混叠滤波再进行抽取。这事抗混叠滤波就可以使用如下CIC多级滤波器进行级联。

上面的图是一级CIC，如果感觉阻带衰减不满足要求，那么可以进行多级CIC滤波器的级联。

理论上多级CIC滤波器可以直接由多个单级CIC滤波器级联得到，但根据 Noble恒等式（“先进行抽取或者插值，再进行线性滤波”与“先进行线性滤波，再进行抽取或者插值”这两者是可以等价的） 。这个公式特别重要也是CIC滤波器在抗混叠滤波器应用如此广泛的另一个原因。所以根据这个原理，当抽取时，我们把抽取操作放到CIC滤波器积分与梳状之间。假设抽取个数与CIC滤波器的阶数相同，那么级联的梳状滤波器正好变成一阶，如下图：
在这里插入图片描述

多级CIC抽取的整个级联图倍简化成上面图形，所以CIC滤波器在抽取中才会那么常用。

多级CIC滤波器的内插操作

上面我们我们已经介绍了CIC滤波器在抽取中的优点以及特殊结构。接下来我们将介绍CIC滤波器在内插中的优点及特殊结构。
常见的内插操作如下：

从上面我们可以看出一般先进行内插再进行抗混叠滤波。这时抗混叠滤波就可以使用如下CIC多级滤波器进行级联。

上面的图是一级CIC，如果感觉阻带衰减不满足要求，那么可以进行多级CIC滤波器的级联。

同样，利用 Noble恒等式，我们可以将内插操作放到梳状滤波器与积分滤波器的中间。假设内插的个数与梳状滤波器的阶数相同，那么将内插操作插入到梳状滤波器之后，便可以将梳状滤波器化简为1阶滤波器。从而减少硬件资源量，变化之后的图形如下图：

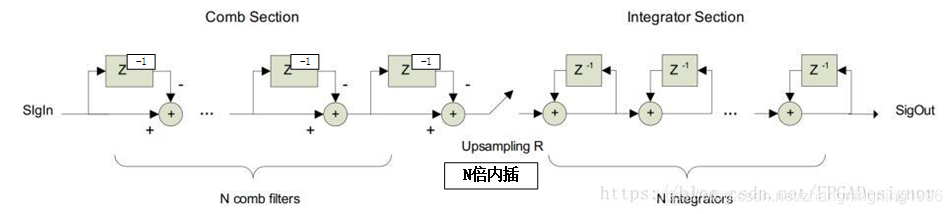
多级CIC滤波器的抽取的MATLAB实现

我们实现的功能是，采样率1MHz，信号2.5KHz的正弦波进行采样，然后将采样之后的信号进行4倍抽取。在这个程序中，我们使用的是3级4阶CIC滤波器级联进行滤波操作。最后对比两个结果。我们严格按照变形之后的图形，即经过Noble恒等式变形之后的图形进行编写MATLAB代码：

close all
clear all
clc
 
%set system parameter
fs = 2500;    %The frequency of the local oscillator signal
Fs = 1000000;   %sampling frequency
N =  24;         %Quantitative bits
L = 50000000;
 
%Generating an input signal
t =0:1/Fs:(1/Fs)*(L-1);          %Generating the time series of sampling frequencies
sc =sin(2*pi*fs*t);        %a sinusoidal input signal that produces a random starting phase
 
b =[1,-1];%integerator
a =[1,-1];%comb 
 
%comb
c1=filter(1,b,sc);
c2=filter(1,b,c1);
c3=filter(1,b,c2);
 
y = downsample(c3,4);
 
%integerater
i1 =filter(a,1,y);
i2 =filter(a,1,i1);
i3 =filter(a,1,i2);
sf = i3;
 
 
 
figure(1),
subplot(211),stem(t(1:1600),sc(1:1600));
xlabel('时间(t)','fontsize',8);
ylabel('幅度(dB)','fontsize',8);
title('sc','fontsize',8);
subplot(212),stem(t(1:400),sf(1:400));
xlabel('时间/4(t)','fontsize',8);
ylabel('幅度(dB)','fontsize',8);
title('sf','fontsize',8);

相信大家经过MATLAB代码与博客理论之间的学习，可以很容易学会CIC滤波器在信号抽取上面的实现。

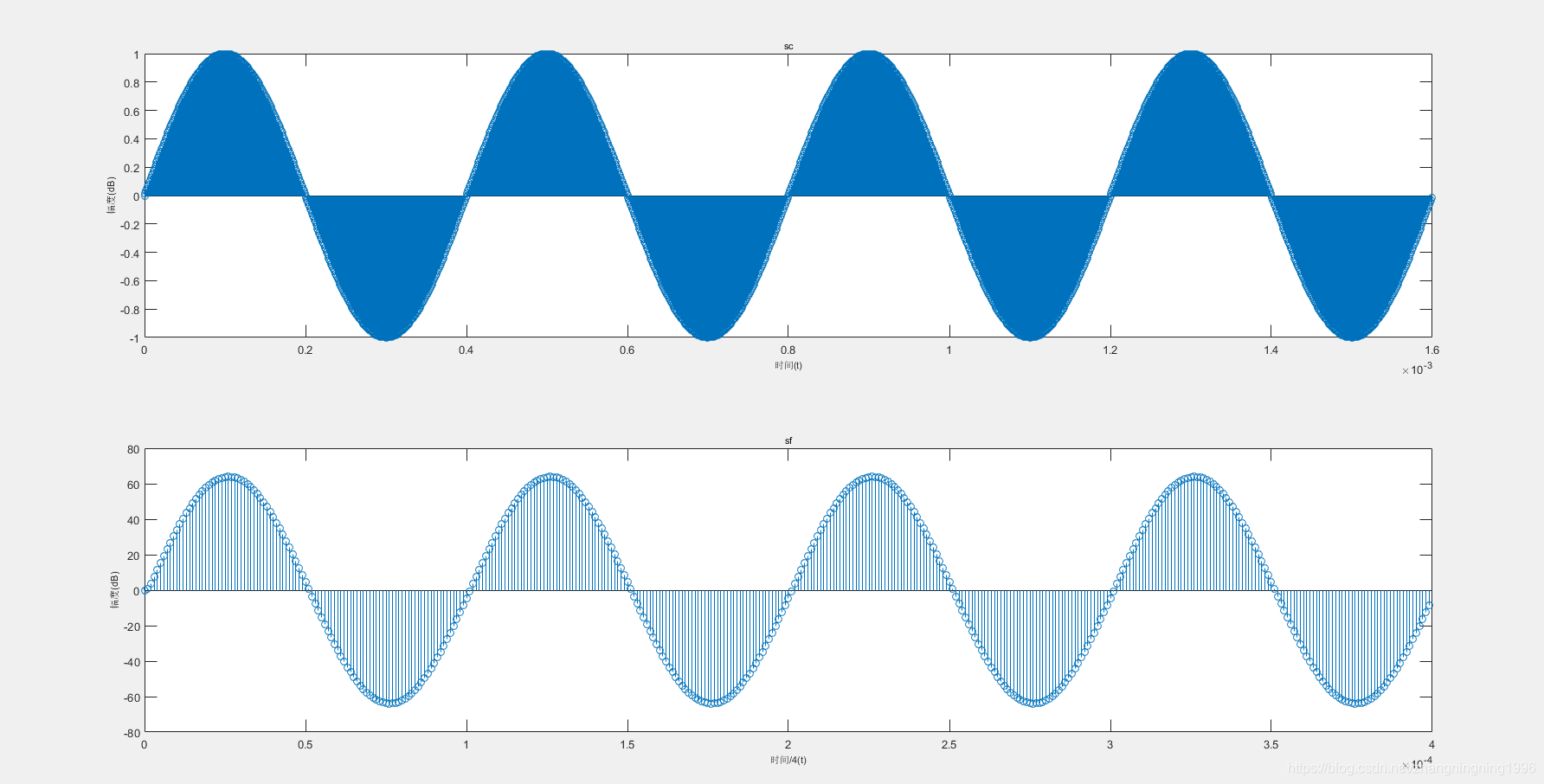
多级CIC滤波器的抽取的MATLAB结果

我们将上面的MATLAB文件进行运行，结果如下：
在这里插入图片描述
从上面的结果可以看出我们成功实现了CIC抽取操作。

多级CIC滤波器的内插的MATLAB实现

我们实现的功能是，采样率0.25MHz，信号2.5KHz的正弦波进行采样，然后将采样之后的信号进行4倍内插。在这个程序中，我们使用的是3级4阶CIC滤波器级联进行滤波操作。我们的内插操作也是按照前面Noble恒等式变形之后的图形进行的程序**。这里需要注意一下，上一篇博客关于单级CIC滤波器的内插操作，我们没有按照变形之后的图像操作，只是把CIC当成了一个简单的低通滤波器来进行信号处理。但是抽取部分吗是严格按照变形之后的图形进行的。**，代码如下：

close all
clear all
clc
 
%set system parameter
fs = 2500;    %The frequency of the local oscillator signal
Fs = 250000;   %sampling frequency
L = 81920;
 
%Generating an input signal
t =0:1/Fs:(1/Fs)*(L-1);          %Generating the time series of sampling frequencies
sc =sin(2*pi*fs*t);        %a sinusoidal input signal that produces a random starting phase
 
b =[1,-1];%comb
a =[1,-1];%integerator
 
%comb
c1=filter(b,1,sc);
c2=filter(b,1,c1);
c3=filter(b,1,c2);
 
y = upsample(c3,4);
 
%integerater
i1 =filter(1,a,y);
i2 =filter(1,a,i1);
i3 =filter