A Plug for UNIX 最大流dinic

题目：

You are in charge of setting up the press room for the inaugural meeting of the United Nations Internet eXecutive (UNIX), which has an international mandate to make the free flow of information and ideas on the Internet as cumbersome and bureaucratic as possible. 
Since the room was designed to accommodate reporters and journalists from around the world, it is equipped with electrical receptacles to suit the different shapes of plugs and voltages used by appliances in all of the countries that existed when the room was built. Unfortunately, the room was built many years ago when reporters used very few electric and electronic devices and is equipped with only one receptacle of each type. These days, like everyone else, reporters require many such devices to do their jobs: laptops, cell phones, tape recorders, pagers, coffee pots, microwave ovens, blow dryers, curling 
irons, tooth brushes, etc. Naturally, many of these devices can operate on batteries, but since the meeting is likely to be long and tedious, you want to be able to plug in as many as you can. 
Before the meeting begins, you gather up all the devices that the reporters would like to use, and attempt to set them up. You notice that some of the devices use plugs for which there is no receptacle. You wonder if these devices are from countries that didn't exist when the room was built. For some receptacles, there are several devices that use the corresponding plug. For other receptacles, there are no devices that use the corresponding plug. 
In order to try to solve the problem you visit a nearby parts supply store. The store sells adapters that allow one type of plug to be used in a different type of outlet. Moreover, adapters are allowed to be plugged into other adapters. The store does not have adapters for all possible combinations of plugs and receptacles, but there is essentially an unlimited supply of the ones they do have.

输入：

The input will consist of one case. The first line contains a single positive integer n (1 <= n <= 100) indicating the number of receptacles in the room. The next n lines list the receptacle types found in the room. Each receptacle type consists of a string of at most 24 alphanumeric characters. The next line contains a single positive integer m (1 <= m <= 100) indicating the number of devices you would like to plug in. Each of the next m lines lists the name of a device followed by the type of plug it uses (which is identical to the type of receptacle it requires). A device name is a string of at most 24 alphanumeric 
characters. No two devices will have exactly the same name. The plug type is separated from the device name by a space. The next line contains a single positive integer k (1 <= k <= 100) indicating the number of different varieties of adapters that are available. Each of the next k lines describes a variety of adapter, giving the type of receptacle provided by the adapter, followed by a space, followed by the type of plug.

输出：

A line containing a single non-negative integer indicating the smallest number of devices that cannot be plugged in.

样例输入：

4 
A 
B 
C 
D 
5 
laptop B 
phone C 
pager B 
clock B 
comb X 
3 
B X 
X A 
X D 

样例输出：

1

题意：

在一个房间里有n种类型的插座，有m种要插入的设备，有k种适配器。求不能插入设备的最小数量。

首先输入n行房间里已经存在的插座类型，再输入m个要插入的设备名称，后面跟着它们使用的插头类型（与他需要的插座类型相同），最后输入k种适配器，给出适配器提供的插座类型以及他的插头类型（比如说 A B 就是把B变成A）

下面给出一张图帮助理解（案例）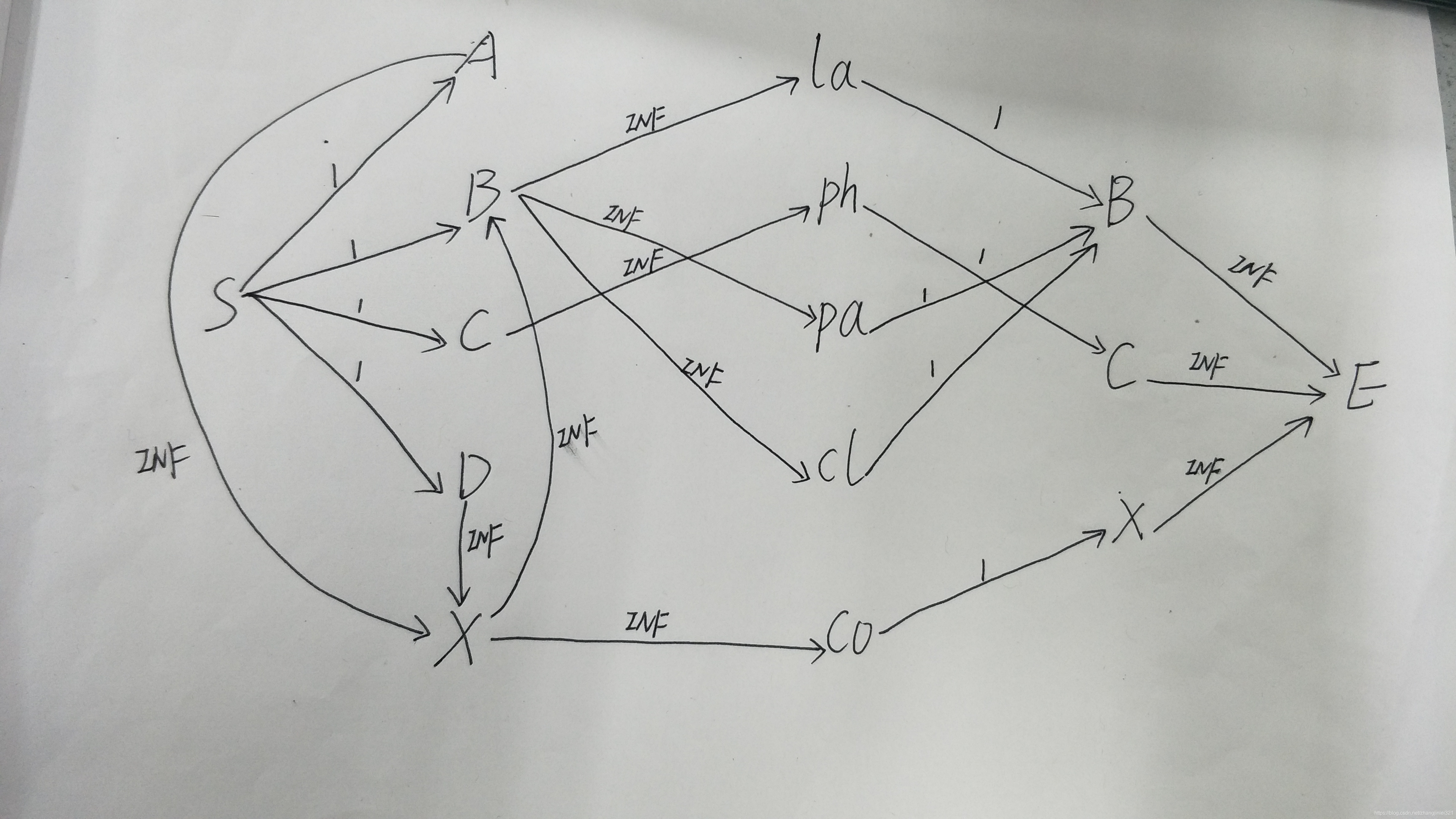

S是超级源点，E是超级汇点，开始用map把房间里已经存在的插座类型储存起来（便于把这些已经存在的类型与设备一一连接）， 由于本来存在的这些插座类型只能使用一次，所以建图的时候源点与他们之间的权值为1，因为每个设备只有一个，所以设备和他匹配的类型之间的权值也为1,。（注：反向弧都为0）

提醒自己，这样的建图方式决定了add要成双成对，别忘了反向弧的存在；入队别忘了出队；

AC代码;

#include <iostream>
#include <cstdio>
#include <cstring>
#include <map>
#include <cmath>
#include <string>
#include <queue>
#include <algorithm>
using namespace std;
const int maxn=100100;
int head[maxn],dis[maxn],cur[maxn];
int cnt;
const int INF=0x7fffffff;
int S,E,n,m,k;
map<string,int>hap;
struct edge
{
    int u,v,c,next;
}node[4*maxn];
void add(int u,int v,int c)
{
    node[cnt].u=u;
    node[cnt].v=v;
    node[cnt].c=c;
    node[cnt].next=head[u];
    head[u]=cnt++;
}
bool bfs()
{
    memset(dis,0,sizeof(dis));
    queue<int>q;
    q.push(S);
    dis[S]=1;
    while(!q.empty())
    {
        int u=q.front();
        q.pop();
        for(int i=head[u];i!=-1;i=node[i].next)
        {
            edge e=node[i];
            if(!dis[e.v]&&e.c>0)
            {
                dis[e.v]=dis[e.u]+1;
                q.push(e.v);
                if(e.v==E) return 1;
            }
        }
    }
    return dis[E]!=0;
}
int dfs(int u,int mx)
{
    int ret=0;
    if(u==E||mx==0) return mx;
    for(int &i=cur[u];i!=-1;i=node[i].next)
    {
        edge e=node[i];
        if(dis[e.v]==dis[e.u]+1&&e.c>0)
        {
            int w=dfs(e.v,min(mx,e.c));
            node[i].c-=w;
            node[i^1].c+=w;
            ret+=w;
            mx-=w;
            if(mx==0)break;
        }
    }
    return ret;
}
int dinic()
{
    int maxflow=0;
    while(bfs())
    {
        memcpy(cur,head,sizeof(head));
        maxflow+=dfs(S,INF);
    }
    return maxflow;
}
int main()
{
        scanf("%d",&n);
        cnt=0;
        memset(head,-1,sizeof(head));
        S=0,E=n+3*m+2*k+1;//超级汇点可以不用非得是这样，只要定义的点以前没出现过就好了

        for(int i=1;i<=n;i++)
        {
            string str1;
            cin>>str1;
            hap[str1]=i;//把已经存在的插座类型用map储存
            add(S,i,1);//超级源点与已经存在的插座类型连接
            add(i,S,0);
        }
        scanf("%d",&m);
        for(int i=1;i<=m;i++)
        {
            string str2,str3;
            cin>>str2>>str3;
            add(n+i,n+m+i,1);//设备与各自的匹配类型连接
            add(n+m+i,n+i,0);
            add(n+m+i,E,INF);//设备所匹配的类型与超级汇点连接
            add(E,n+m+i,0);
            if(!hap[str3])//如果设备匹配的这些类型中开始不存在的话，就给他定义一个点
            {
                hap[str3]=n+2*m+i;
            }
            add(hap[str3],n+i,INF);//将已经存在的插座类型与他匹配的设备连接
            add(n+i,hap[str3],0);
        }
        scanf("%d",&k);
        for(int i=1;i<=k;i++)
        {
            string str4,str5;
            cin>>str4>>str5;
            if(!hap[str4])hap[str4]=n+3*m+i;//这两句与上面的if意思一样
            if(!hap[str5])hap[str5]=n+3*m+k+i;
            add(hap[str5],hap[str4],INF);//将这些适配器连接起来
            add(hap[str4],hap[str5],0);
        }
        printf("%d\n",m-dinic());//因为要输出不能插入的设备的最小数量，而我们求的是能插入的设备的数量，所以要用设备总数量m减去能插入的，剩下的就是不能插入的

    return 0;
}