【高等数学+求极限+最大公约数GCD】HDU-6668 Polynomial

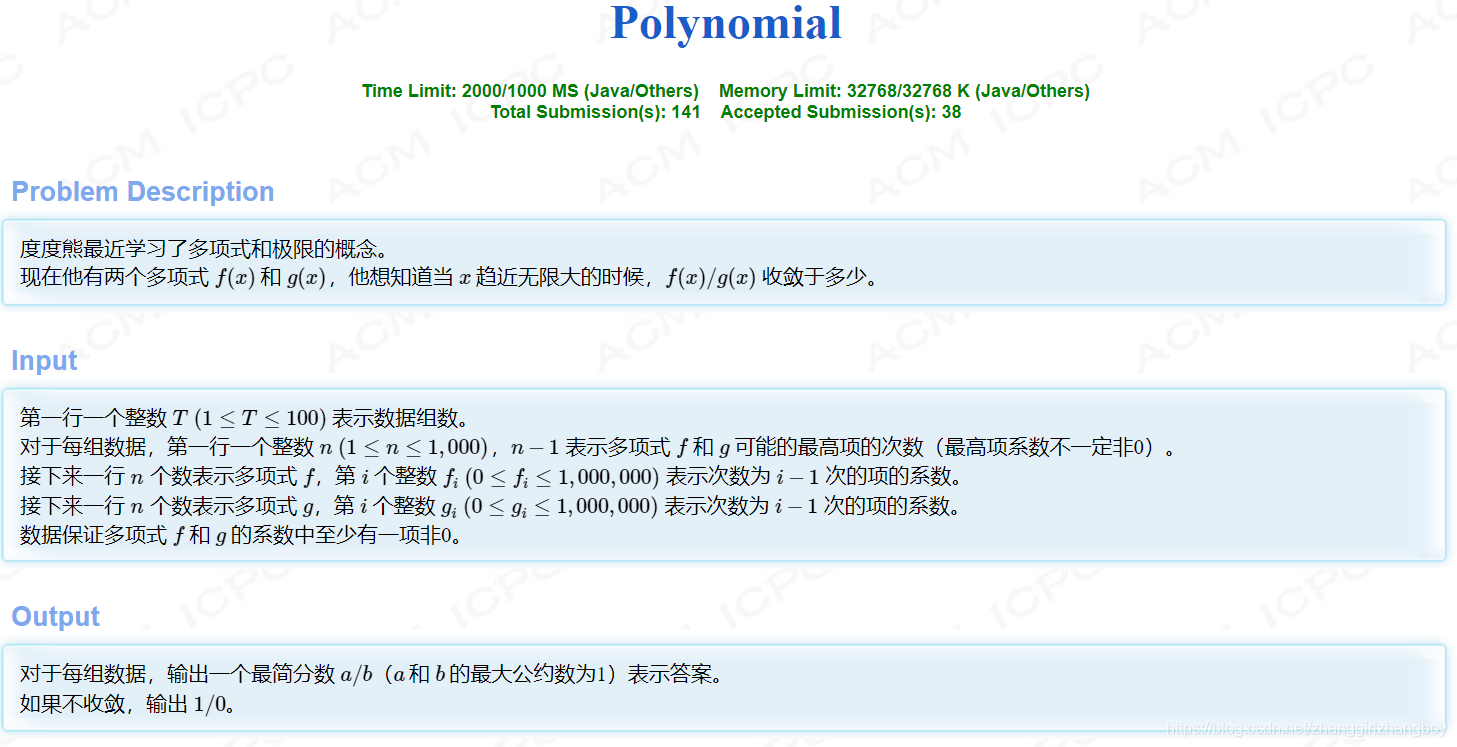
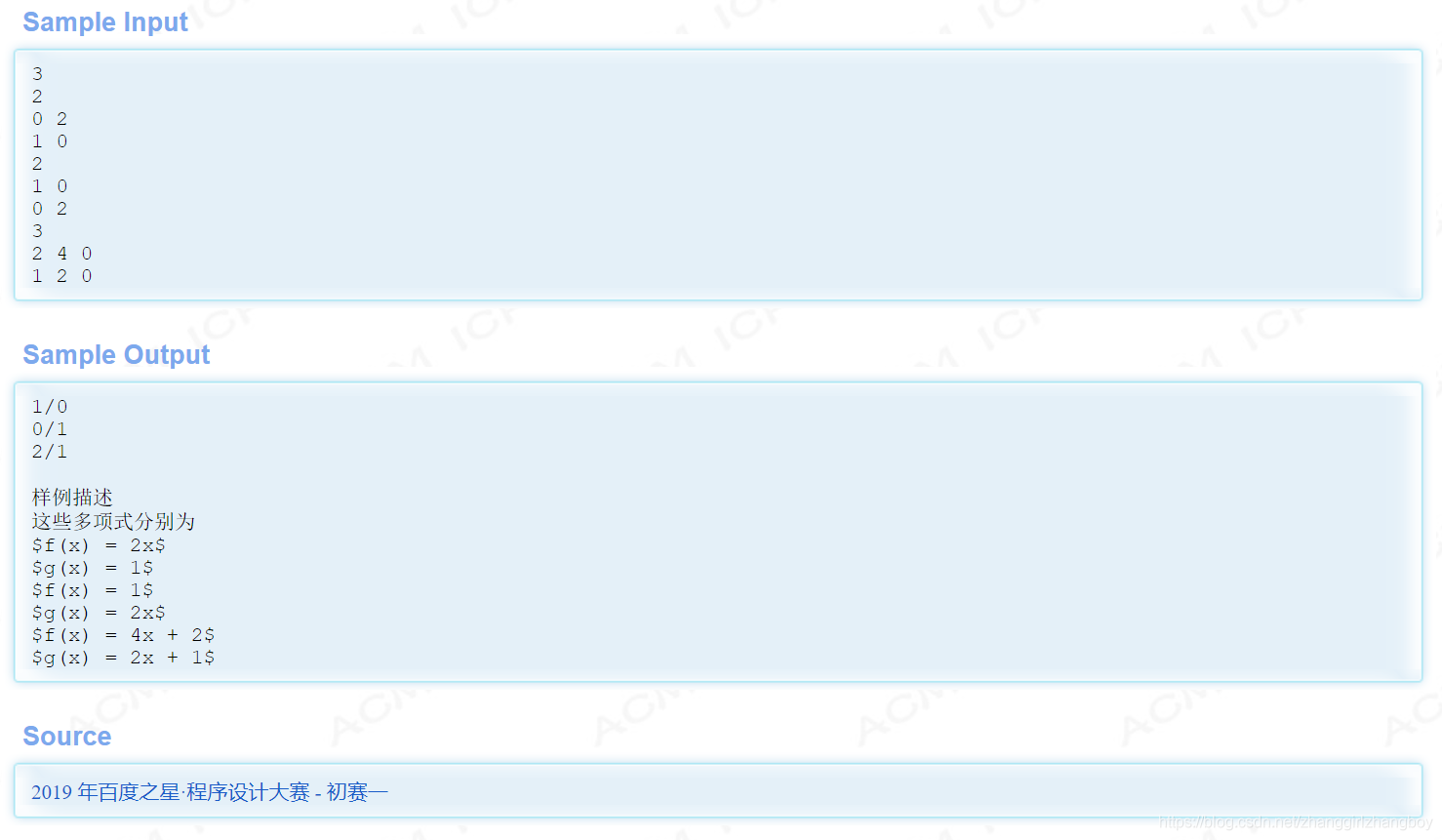
注解

1、高等数学求极限。分式求极限，只需要找到最高次项，分母次数高，则极限为0，分子次数高，则极限为无穷。分母分子次数相同，极限就是二者系数之比。
2、欧几里得算法求最大公约数GCD，用于化简分数。
3、注意数据范围。最好用long long int避免中间结果溢出。

代码

#include <iostream>

using namespace std;

typedef long long int LL;

LL gcd(LL a, LL b){
	return a%b==0?b:gcd(b, a%b);
}

int main(){
	int T;
	cin>>T;
	for(int i=0; i<T; i++){
		LL n;
		cin>>n;
		LL f, g = 0;
		LL fpos, gpos = -1;
		LL tmp;
		for(int j=0; j<n; j++){
			cin>>tmp;
			if(tmp){
				f = tmp;
				fpos = j;
			}
		}
		for(int j=0; j<n; j++){
			cin>>tmp;
			if(tmp){
				g = tmp;
				gpos = j;
			}
		}
		if(fpos>gpos){
			cout<<"1/0"<<endl;
		}
		else if(fpos<gpos){
			cout<<"0/1"<<endl;
		}
		else{
			tmp = gcd(f, g);
			cout<<f/tmp<<"/"<<g/tmp<<endl;
		}
	}
	return 0;
}

结果