【动态规划dp+最长公共子序列+字符串处理】HDU-1080 Human Gene Functions-优快云博客

本文介绍了一种使用动态规划算法解决最长公共子序列问题的方法，通过矩阵dp进行状态转移，考虑了三种情况：不含空格、第一个字符含空格、第二个字符含空格。代码中使用了C++实现，包括初始化矩阵、状态转移方程和最终结果输出。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

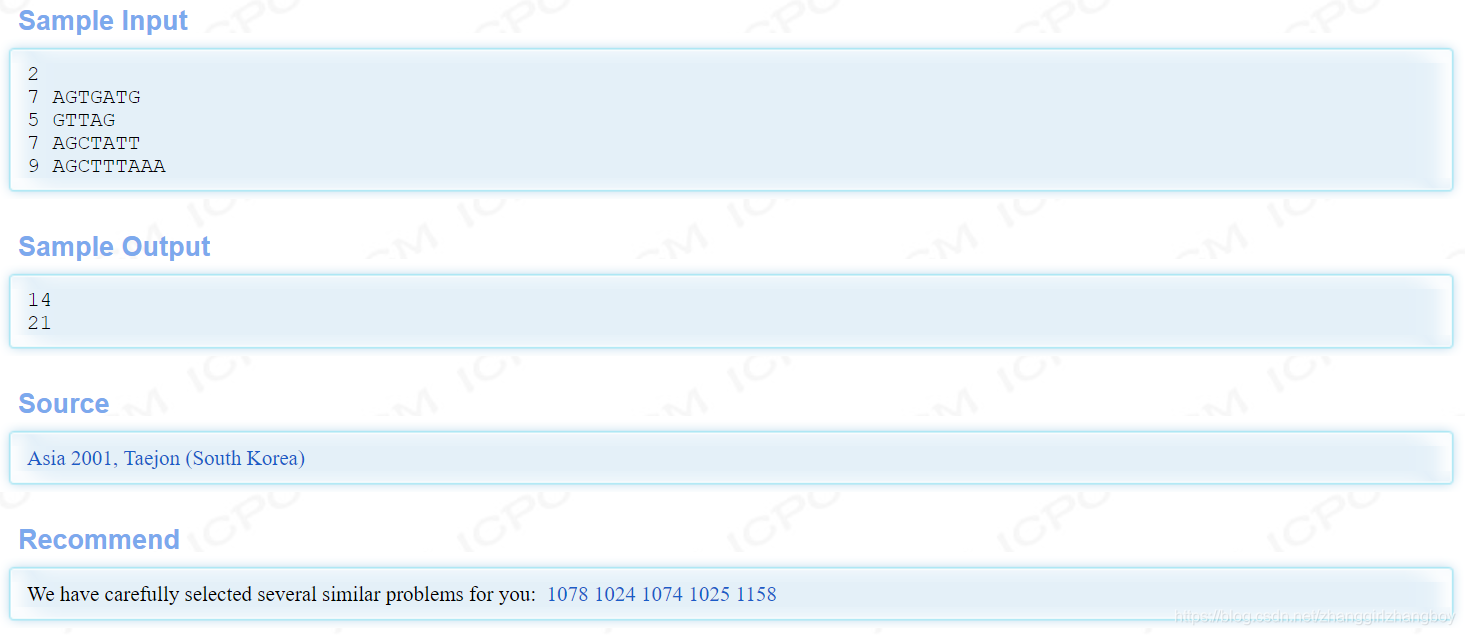
在这里插入图片描述

注解

1、动态规划，最长公共子序列，三种情况：（不含空格，第一个字符含空格，第二个字符含空格）

dp[j][k] = max(dp[j][k], dp[j-1][k-1]+A[index][index2]);
dp[j][k] = max(dp[j][k], dp[j-1][k]+A[index][4]);
dp[j][k] = max(dp[j][k], dp[j][k-1]+A[4][index2]);

2、类似于最长公共子序列的做法。
3、字符串处理：find方法等。

代码

#include <iostream>
#include <cstring>

using namespace std;

int A[5][5] = {{5, -1, -2, -1, -3},
    {-1, 5, -3, -2, -4},
    {-2, -3, 5, -2, -2},
    {-1, -2, -2, 5, -1},
    {-3, -4, -2, -1, -100}
};
string str = "ACGT";

int main() {
    int T;
    cin>>T;
    for(int i=0; i<T; i++) {
        int len1, len2;
        string s1, s2;
        cin>>len1>>s1;
        cin>>len2>>s2;
        int dp[len1+1][len2+1];
        memset(dp, 0, sizeof(dp));
        for(int j=0; j<len1; j++) {
            int index = str.find(s1.at(j));
            dp[j+1][0] = dp[j][0] + A[index][4];
        }
        for(int j=0; j<len2; j++) {
            int index = str.find(s2.at(j));
            dp[0][j+1] = dp[0][j] + A[4][index];
        }
        for(int j=1; j<len1+1; j++) {
            for(int k=1; k<len2+1; k++) {
                int index = str.find(s1.at(j-1));
                int index2 = str.find(s2.at(k-1));
                dp[j][k] = -100000;
                dp[j][k] = max(dp[j][k], dp[j-1][k-1]+A[index][index2]);
                dp[j][k] = max(dp[j][k], dp[j-1][k]+A[index][4]);
                dp[j][k] = max(dp[j][k], dp[j][k-1]+A[4][index2]);
            }
        }
        cout<<dp[len1][len2]<<endl;
    }
    return 0;
}

结果

在这里插入图片描述