【小Y学算法】⚡️每日LeetCode打卡⚡️——29.将有序数组转换为二叉搜索树-优快云博客

本文介绍了如何将有序数组转换为高度平衡的二叉搜索树，提供了C#和两种Java解法，包括中序遍历选择中间元素作为根节点。方法详细解释了思路并分析了时间复杂度和空间复杂度。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

请添加图片描述

📢前言

🚀 算法题 🚀

🌲 每天打卡一道算法题，既是一个学习过程，又是一个分享的过程😜
🌲 提示：本专栏解题编程语言一律使用 C# 和 Java 两种进行解题
🌲 要保持一个每天都在学习的状态，让我们一起努力成为算法大神吧🧐！
🌲 今天是力扣算法题持续打卡第29天🎈！

🚀 算法题 🚀

🌲原题样例：将有序数组转换为二叉搜索树

给你一个整数数组 nums ，其中元素已经按升序排列，请你将其转换为一棵高度平衡二叉搜索树。

高度平衡二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。

示例 1：
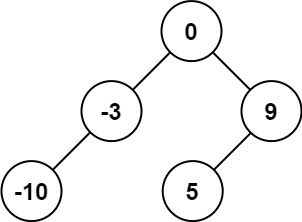
在这里插入图片描述
输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：

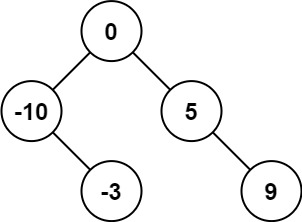
示例 2：

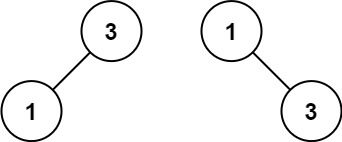
输入：nums = [1,3]
输出：[3,1]
解释：[1,3] 和 [3,1] 都是高度平衡二叉搜索树。

提示：

1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 按严格递增顺序排列

🌻C#方法：中序遍历

关于二叉搜索树的含义，这里那力扣的解释来给大家参考看一下
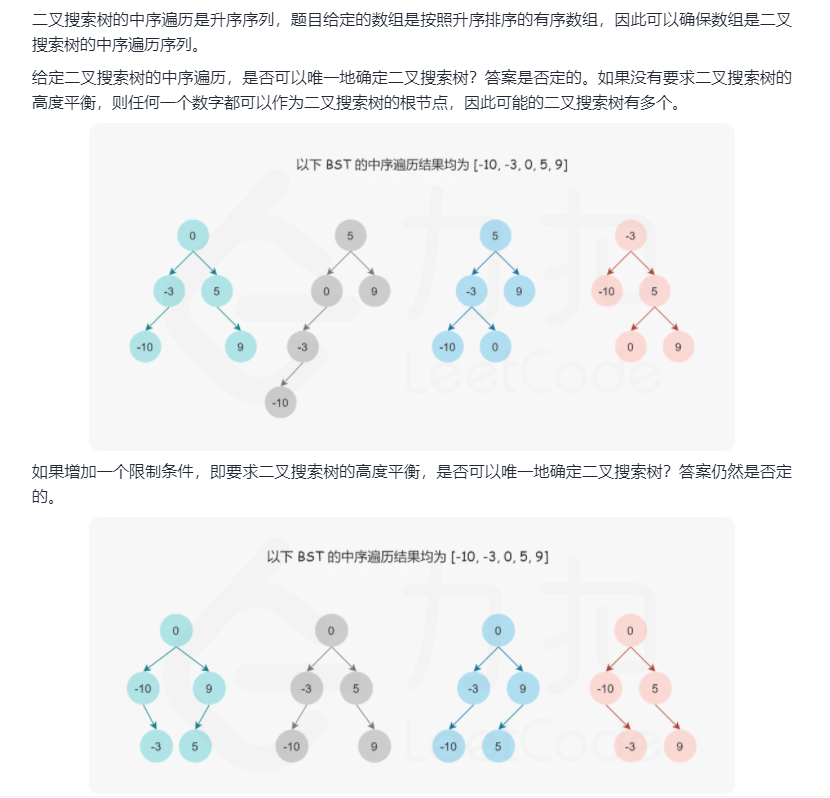
在这里插入图片描述

思路解析
中序遍历，总是选择中间位置左边的数字作为根节点

选择中间位置左边的数字作为根节点，则根节点的下标为 mid=(left+right)/2，此处的除法为整数除法。

代码：

public class Solution {
    static bool func(TreeNode x, TreeNode y) {
        if (x == null) {
            return y == null;
        }

        if (y == null || x.val != y.val) {
            return false;
        }

        return func(x.left, y.right) && func(x.right, y.left);
    }


    public bool IsSymmetric(TreeNode root) {
        return root == null ? true : func(root.left, root.right);
    }
}

执行结果

通过
执行用时：92 ms，在所有 C# 提交中击败了59.72%的用户
内存消耗：25.1 MB，在所有 C# 提交中击败了22.92%的用户

复杂度分析

时间复杂度：O( n ),其中 n 是数组的长度。每个数字只访问一次。
空间复杂度：O(log n )，其中 n 是数组的长度。空间复杂度不考虑返回值，因此空间复杂度主要取决于递归栈的深度，递归栈的深度是O(logn)。

🌻Java 方法一：中序遍历

思路解析

总是选择中间位置左边的数字作为根节点

选择中间位置左边的数字作为根节点，则根节点的下标为 mid=(left+right)/2，此处的除法为整数除法。

代码：

class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        return helper(nums, 0, nums.length - 1);
    }

    public TreeNode helper(int[] nums, int left, int right) {
        if (left > right) {
            return null;
        }

        // 总是选择中间位置左边的数字作为根节点
        int mid = (left + right) / 2;

        TreeNode root = new TreeNode(nums[mid]);
        root.left = helper(nums, left, mid - 1);
        root.right = helper(nums, mid + 1, right);
        return root;
    }
}

执行结果

通过
执行用时：0 ms，在所有 Java  提交中击败了100.00%的用户
内存消耗：38.2 MB，在所有 Java 提交中击败了36.59%的用户

复杂度分析

时间复杂度：O( n ),其中 n 是数组的长度。每个数字只访问一次。
空间复杂度：O(log n )，其中 n 是数组的长度。空间复杂度不考虑返回值，因此空间复杂度主要取决于递归栈的深度，递归栈的深度是O(logn)。

🌻Java 方法二：中序遍历，选择任意一个中间位置数字作为根节点

思路解析

选择任意一个中间位置数字作为根节点，则根节点的下标为mid=(left+right)/2 和 mid=(left+right+1)/2

两者中随机选择一个，此处的除法为整数除法。

代码：

class Solution {
    public void merge(int[] nums1, int m, int[] nums2, int n) {
        int p1 = 0, p2 = 0;
        int[] sorted = new int[m + n];
        int cur;
        while (p1 < m || p2 < n) {
            if (p1 == m) {
                cur = nums2[p2++];
            } else if (p2 == n) {
                cur = nums1[p1++];
            } else if (nums1[p1] < nums2[p2]) {
                cur = nums1[p1++];
            } else {
                cur = nums2[p2++];
            }
            sorted[p1 + p2 - 1] = cur;
        }
        for (int i = 0; i != m + n; ++i) {
            nums1[i] = sorted[i];
        }
    }
}

执行结果

通过
执行用时：0 ms，在所有 Java  提交中击败了100.00%的用户
内存消耗：38.3 MB，在所有 Java 提交中击败了18.28%的用户

复杂度分析

时间复杂度：O(n)
空间复杂度：O(log n)

💬总结

今天是力扣算法题打卡的第二十九天！
文章采用 C#和 Java 两种编程语言进行解题
一些方法也是参考力扣大神写的，也是边学习边分享，再次感谢算法大佬们
那今天的算法题分享到此结束啦，明天再见！

【小Y学算法】⚡️每日LeetCode打卡⚡️——29.将有序数组转换为二叉搜索树

📢前言

🌲原题样例：将有序数组转换为二叉搜索树

🌻C#方法：中序遍历

🌻Java 方法一：中序遍历

🌻Java 方法二：中序遍历，选择任意一个中间位置数字作为根节点

💬总结

🚀往期优质文章分享