遗传算法1：原理与应用

---

前言

遗传算法（Genetic Algorithm，GA）是一种模拟自然进化过程的随机搜索算法，主要用于优化问题求解。

---

一、基本原理

1.类比生物进化

遗传算法的灵感来源于达尔文的生物进化论。在自然界中，生物通过遗传、变异和自然选择不断进化。在算法中，将问题的解看作是生物个体，解的质量（适应度）类似于生物个体对环境的适应能力。例如，在一个寻找函数最大值的问题中，函数值越高的解就相当于在自然环境中更适应生存的生物个体。

2.主要操作步骤

① *初始化种群：*首先，随机生成一组初始解（个体），这些个体构成了初始种群。种群规模（个体数量）是算法的一个参数，比如可以设置为 100。每个个体通常用一串二进制码（基因编码）或者其他数据结构来表示。

② *评估适应度：*计算每个个体的适应度，适应度函数是根据问题的目标来定义的。例如，在一个旅行商问题（TSP）中，适应度函数可以是旅行路线的总长度，总长度越短，适应度越高。

③*选择操作：*根据个体的适应度，选择一些个体作为父代来产生下一代。常用的选择方法有轮盘赌选择。就像在一个抽奖轮盘中，适应度高的个体在轮盘中所占的面积比例大，被选中的概率也就高。例如，有个体 A、B、C，其适应度分别为 0.2、0.5、0.3，那么个体 B 被选中作为父代的概率相对较高。

④*交叉操作：*选择出来的父代个体通过交叉操作来产生新的个体。比如在二进制编码中，简单的单点交叉是在两个父代个体的基因序列中随机选择一个交叉点，然后交换交叉点之后的部分基因。假设父代个体 1 的基因编码是 1010，父代个体 2 的基因编码是 0101，交叉点选择在第二个位置，那么交叉后产生的两个新个体的基因编码分别是 1101 和 0010。

⑤*变异操作：*新个体有一定概率发生变异，改变其基因。在二进制编码中，变异就是将基因中的某一位（0 变为 1 或者 1 变为 0）进行改变。变异操作可以增加种群的多样性，避免算法过早收敛到局部最优解。例如，一个个体的基因编码是 1010，在某一变异概率下，第三位的 1 可能变异为 0，变成 1000。

⑥*重复操作：*经过选择、交叉和变异操作后，得到新一代种群，然后对新一代种群重复评估适应度、选择、交叉和变异等操作，直到满足终止条件。终止条件可以是达到一定的迭代次数，或者种群的适应度达到了某个设定的阈值。

常规流程图如下：

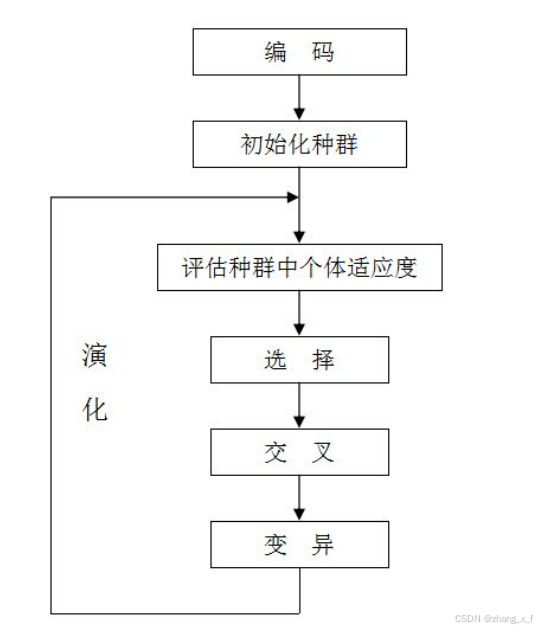
二、应用领域

1.工程优化

在机械设计中，可以用遗传算法来优化机械结构的参数。例如，寻找汽车发动机的最佳设计参数，如气缸直径、活塞行程等，以提高发动机的功率和燃油效率。通过定义适应度函数为发动机性能指标，经过多次迭代，遗传算法可以找到一组较优的参数组合。

2.人工智能和机器学习

在神经网络的结构和参数优化方面发挥作用。比如优化神经网络的权重和神经元连接方式。以图像识别神经网络为例，利用遗传算法调整神经网络的参数，使网络对图像的识别准确率更高。

3.组合优化问题

例如：旅行商问题是典型的组合优化问题，即给定一组城市和它们之间的距离，寻找一条最短的遍历所有城市的路线。遗传算法可以有效地处理这类问题，通过不断进化种群，找到接近最优的旅行路线。

示例代码（Python实现）以下是一个简单的遗传算法实现，用于求解函数f(x)=x **2 的最小值：

import random

# 目标函数
def fitness(x):
    return x**2

# 初始化种群
def initialize_population(pop_size, chrom_length):
    return [random.uniform(-10, 10) for _ in range(pop_size)]

# 选择
def selection(population, fitness_values):
    total_fitness = sum(fitness_values)
    probabilities = [f/total_fitness for f in fitness_values]
    selected = random.choices(population, weights=probabilities, k=len(population))
    return selected

# 交叉
def crossover(parent1, parent2):
    alpha = random.random()
    child1 = alpha * parent1 + (1 - alpha) * parent2
    child2 = alpha * parent2 + (1 - alpha) * parent1
    return child1, child2

# 变异
def mutate(individual, mutation_rate):
    if random.random() < mutation_rate:
        return individual + random.uniform(-1, 1)
    return individual

# 遗传算法主函数
def genetic_algorithm(pop_size, chrom_length, generations, mutation_rate):
    population = initialize_population(pop_size, chrom_length)
    for _ in range(generations):
        fitness_values = [fitness(x) for x in population]
        population = selection(population, fitness_values)
        new_population = []
        for i in range(0, pop_size, 2):
            parent1, parent2 = population[i], population[i+1]
            child1, child2 = crossover(parent1, parent2)
            new_population.append(mutate(child1, mutation_rate))
            new_population.append(mutate(child2, mutation_rate))
        population = new_population
    return min(population, key=fitness)

# 运行算法
result = genetic_algorithm(pop_size=50, chrom_length=1, generations=100, mutation_rate=0.1)
print("最优解：", result)

三、优点和局限性

1.优点

具有较强的全局搜索能力，能够在复杂的搜索空间中找到较优的解。它不依赖于问题的梯度信息，适用于非连续、不可微的函数优化问题。而且它可以并行处理，同时对多个解进行操作，提高搜索效率。

2.局限性

计算复杂度较高，尤其是在处理大规模问题或者复杂的适应度函数时。另外，算法的性能依赖于参数的设置，如种群规模、交叉概率和变异概率等，如果参数设置不当，可能会导致算法收敛过慢或者陷入局部最优解。

• 遗传算法是一种强大的全局优化工具，适用于多种复杂问题。通过合理设计编码方式、适应度函数和操作策略，可以显著提高算法的性能。