粒子群算法（PSO）-燃烧反应动力学

原创于 2024-10-21 16:02:40 发布 · 1k 阅读

25 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #python

文章目录

提示1：此篇只概述理论，后续再叙述粒子群算法在燃烧反应机理简化中的思想
提示2：文章内容仅供参考

概要

**粒子群优化算法(PSO)：**是1995 年由Eberhart 博士和kennedy 博士提出，源于对鸟群捕食的行为研究。该算法最初是受到飞鸟集群活动的规律性启发，进而利用群体智能建立的一个简化模型。粒子群算法在对动物集群活动行为观察基础上，利用群体中的个体对信息的共享使整个群体的运动在问题求解空间中产生从无序到有序的演化过程，从而获得最优解。
**粒子群算法的优势：**在于简单容易实现并且没有许多参数的调节。目前已被广泛应用于函数优化、神经网络训练、模糊系统控制以及其他遗传算法的应用领域。

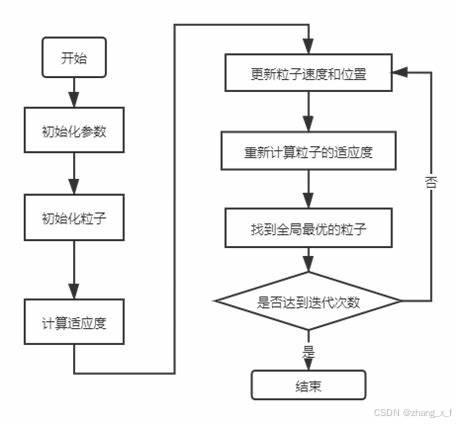
整体流程

初始化：
- 随机初始化一群粒子（候选解），每个粒子代表问题的一个潜在解。
- 为每个粒子分配一个随机位置和速度。
- 计算每个粒子的适应度（目标函数值）。
设置个体和全局最优：
- 对于每个粒子，记录其找到的最优位置（个体最优，记为pbest）。
- 确定整个粒子群中所有粒子的最优位置（全局最优，记为gbest）。
迭代过程：
- 对于每次迭代：
  a. 更新速度：根据当前位置、个体最优位置和全局最优位置，更新每个粒子的速度。速度更新公式通常如下：
  
  b. 更新位置：根据新的速度更新每个粒子的位置。
  
  c. 边界处理：如果粒子的位置超出了搜索空间的边界，将其调整到边界上。
  d. 评估适应度：计算每个粒子的新位置的适应度。
  e. 更新个体和全局最优：如果粒子的新位置比其个体最优位置更好，则更新个体最优位置。如果粒子的新位置比全局最优位置更好，则更新全局最优位置。
终止条件：
- 检查是否满足终止条件，如达到最大迭代次数、适应度达到预设阈值或运行时间限制。
- 如果满足终止条件，则算法结束；否则，返回步骤3继续迭代。
输出结果：
- 输出全局最优位置gbest作为问题的最优解。
PSO算法以其简单、易于实现和较强的全局搜索能力而被广泛应用于各种优化问题。然而，它也可能遇到早熟收敛的问题，即粒子过早地聚集在非最优解附近，导致搜索能力下降。为了解决这个问题，研究者们提出了多种改进策略，如调整惯性权重、引入混合策略等。

技术名词解释

粒子群优化（Particle Swarm Optimization, PSO）算法中涉及的一些关键名词解释如下：

粒子（Particle）：
- 粒子是算法中的一个基本单位，代表问题的潜在解。每个粒子在搜索空间中有自己的位置和速度。
位置（Position）：
- 粒子在搜索空间中的具体坐标，代表了粒子当前的解。
速度（Velocity）：
- 粒子在搜索空间中移动的速度和方向，决定了粒子位置的更新。
适应度（Fitness）：
- 根据目标函数计算的粒子性能的度量，用于评价粒子解的质量。
个体最优（Personal Best, pBest）：
- 每个粒子在搜索过程中所找到的最优解，即该粒子历史上的最佳位置。
全局最优（Global Best, gBest）：
- 整个粒子群中所有粒子所找到的最优解，即整个群体历史上的最佳位置。
惯性权重（Inertia Weight, w）：
- 控制粒子速度的前一次迭代值对当前速度的影响程度。较大的惯性权重可以使粒子保持原有的搜索方向，较小的惯性权重则使粒子更容易受到个体最优和全局最优的影响。
学习因子（Learning Factors）：
- 通常用( c1 )和( c2)表示，它们是两个加速常数，分别影响粒子向个体最优和全局最优移动的趋势。
随机数（Random Numbers）：
- 在更新粒子速度和位置时引入的随机性，以增加搜索的多样性，通常用( r1 )和( r2 )表示。
搜索空间（Search Space）：
- 问题解的所有可能值构成的空间，粒子在其中搜索最优解。
迭代（Iteration）：
- 算法执行的重复过程，每次迭代中，所有粒子都会更新自己的位置和速度。
终止条件（Termination Condition）：
- 算法停止执行的条件，可以是达到最大迭代次数、解的质量达到某个阈值，或者超过预定的计算时间等。
早熟收敛（Premature Convergence）：
- 粒子群算法在搜索过程中可能遇到的问题，即粒子过早地集中在一个非全局最优的区域，导致搜索范围缩小，无法找到真正的全局最优解。
速度限制（Velocity Limits）：
- 为了控制粒子的搜索范围和避免早熟收敛，可以对粒子的速度设置上限和下限。
拓扑结构（Topology）：
- 粒子群算法中粒子之间的相互关系，可以是全连接、环形、星形等不同的结构，影响粒子信息的共享方式。

粒子群算法在燃烧反应动力学的应用

燃烧模型参数优化：PSO可以用来优化燃烧模型的参数，如活化能和指前因子。通过机器学习方法，如径向基函数插值算法，结合PSO对燃烧机理参数进行优化，可以显著提高燃烧模型在宽工况范围内的预测准确性。例如，对CH4燃烧机理的优化，可以显著降低点火延迟时间和层流火焰速度的预测误差。
燃烧器温度控制：PSO算法被用于优化燃烧器的温度控制系统。通过PSO优化模糊PID控制器的权重因子，可以快速整定模糊PID参数，提高燃烧器温度控制的响应速度和稳定性。
实验设计与模型优化：PSO算法可以用于实验设计的优化，通过聚类分析和实验设计，提高燃烧反应动力学模型的预测能力。例如，通过OptEx平台，实现了大规模实验数据聚类和模型优化，为发展可预测性燃烧反应动力学模型提供了新的思路。
燃烧反应动力学模型分析：PSO算法可以与神经网络结合，用于加速燃烧反应动力学模型的全局灵敏性分析。通过ANN-HDMR方法，可以显著减少动力学模拟的次数，提高分析效率。
燃烧过程的优化控制：PSO算法可以用于火力发电厂锅炉燃烧过程的优化控制，通过优化锅炉燃烧的运行参数，降低发电煤耗和氮氧化合物的排放。
燃烧实验数据的分析：PSO算法可以用于分析燃烧实验数据，如通过粒子群优化的RBF神经网络模型，对锅炉燃烧过程中的输入变量和输出变量进行优化，提高燃烧效率。

小结（PSO优缺点）

粒子群算法（PSO）在燃烧反应动力学中的应用具有以下优缺点：

优点：

简单易实现：PSO算法的基本思想简单，易于理解和编程实现。
全局搜索能力强：PSO算法具有较好的全局搜索能力，能够在复杂的搜索空间中找到较好的解。
适用于多维、非线性、非凸优化问题：PSO算法适用于连续优化问题和离散优化问题，可以应用于多种领域。
提高燃烧效率：通过优化燃烧器的温度控制参数，PSO算法可以提高燃烧效率，减少能源浪费。
减少调整时间：PSO算法可以快速整定模糊PID参数，减少达到稳态的时间。
提高响应速度和稳定性：PSO算法优化的模糊PID控制器可以提高系统的响应速度，减小超调量，增强系统的稳定性。

缺点：

对参数敏感：PSO算法中的参数设置对算法性能影响较大，需要经验调参。
可能陷入局部最优：PSO算法容易陷入局部最优解，对于复杂问题可能无法找到全局最优解。
需要大量迭代次数：PSO算法通常需要较多的迭代次数才能达到较好的结果，计算时间较长。
早熟收敛问题：PSO算法在求解优化问题时易于陷入局部最优，存在早熟收敛的问题。
对问题的解空间分布敏感：如果解空间分布不均匀，可能会导致搜索效率低下。
在燃烧反应动力学中，PSO算法已经被用于燃烧模型参数优化、燃烧器温度控制、实验设计与模型优化等方面，但同时也需要注意其在应用中可能遇到的问题，如参数调整和早熟收敛等。