目录
(1)怎么输出均值 μ 和方差(或 logσ²)这两个参数?
1.CVAE 完整流程拆解(以 “生成指定品种的猫图片” 为例)
(1) Observed data(观测数据)+ Condition(条件变量):双输入组合
(2) Encoder(编码器):基于 “x+c” 输出隐分布参数
(3) Reparameter(重参数化):逻辑不变,z 的分布受 c 约束
(4) Latent vector(隐向量):条件化的概率隐向量
(5) Decoder(解码器):基于 “z+c” 重构 / 生成数据
一.自编码器(AE-autoencoder)核心思想
自编码器部分摘自该文章(40 封私信 / 11 条消息) 【全】一文带你了解自编码器(AutoEncoder) - 知乎
1.构成介绍
暂且不谈神经网络、深度学习等,仅仅是自编码器的话,其原理其实很简单。自编码器可以理解为一个试图去还原其原始输入的系统。自编码器模型如下图所示。
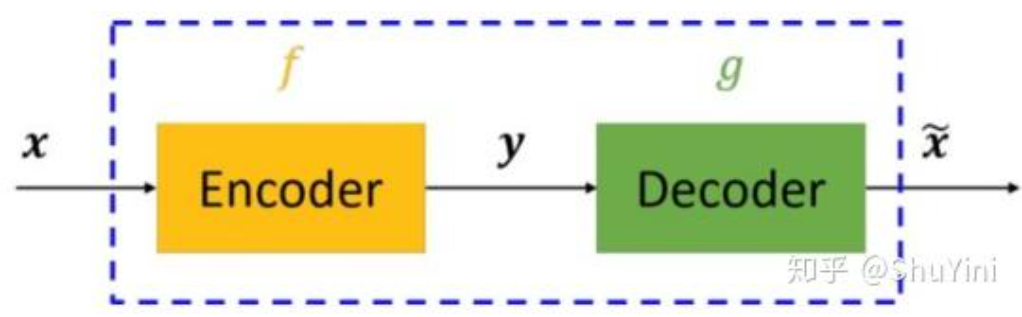
从上图可以看出,自编码器模型主要由编码器(Encoder)和解码器(Decoder)组成,其主要目的是将输入x转换成中间变量y,然后再将y转换成,然后对比输入x和输出
使得他们两个无限接近。
2.神经网络自编码模型
在深度学习中,自动编码器是一种无监督的神经网络模型,它可以学习到输入数据的隐含特征,这称为编码(coding),同时用学习到的新特征可以重构出原始输入数据,称之为解码(decoding)。从直观上来看,自动编码器可以用于特征降维,类似主成分分析PCA,但是其相比PCA其性能更强,这是由于神经网络模型可以提取更有效的新特征。除了进行特征降维,自动编码器学习到的新特征可以送入有监督学习模型中,所以自动编码器可以起到特征提取器的作用。举个例子,我有一张清晰图片,首先我通过编码器压缩这张图片的大小(如果展现出来可能比较模型),然后在需要解码的时候将其还原成清晰的图片。具体过程如下图所示。
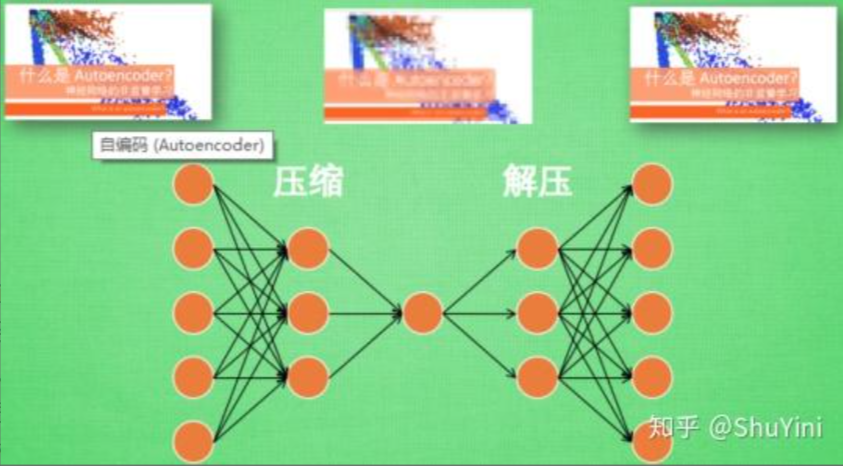
那么此时可能会有人问了,好端端的图片为什么要压缩呢?其主要原因是:有时神经网络要接受大量的输入信息, 比如输入信息是高清图片时, 输入信息量可能达到上千万, 让神经网络直接从上千万个信息源中学习是一件很吃力的工作. 所以, 何不压缩一下, 提取出原图片中的最具代表性的信息, 缩减输入信息量, 再把缩减过后的信息放进神经网络学习. 这样学习起来就简单轻松了. 所以, 自编码就能在这时发挥作用. 通过将原数据白色的X 压缩, 解压 成黑色的X, 然后通过对比黑白 X ,求出预测误差, 进行反向传递, 逐步提升自编码的准确性. 训练好的自编码中间这一部分就是能总结原数据的精髓. 可以看出, 从头到尾, 我们只用到了输入数据 X, 并没有用到 X 对应的数据标签, 所以也可以说自编码是一种非监督学习. 到了真正使用自编码的时候. 通常只会用到自编码前半部分。
3.神经网络自编码器三大特点
- 1、自动编码器是数据相关的(data-specific 或 data-dependent),这意味着自动编码器只能压缩那些与训练数据类似的数据。比如,使用人脸训练出来的自动编码器在压缩别的图片,比如树木时性能很差,因为它学习到的特征是与人脸相关的。
- 2、自动编码器是有损的,意思是解压缩的输出与原来的输入相比是退化的,MP3,JPEG等压缩算法也是如此。这与无损压缩算法不同。
- 3、自动编码器是从数据样本中自动学习的,这意味着很容易对指定类的输入训练出一种特定的编码器,而不需要完成任何新工作。
4.自编码器(Autoencoder)搭建
搭建一个自动编码器需要完成下面三样工作:搭建编码器,搭建解码器,设定一个损失函数,用以衡量由于压缩而损失掉的信息。编码器和解码器一般都是参数化的方程,并关于损失函数可导,典型情况是使用神经网络。编码器和解码器的参数可以通过最小化损失函数而优化,例如SGD。举个例子:根据上面介绍,自动编码器看作由两个级联网络组成。
第一个网络是一个编码器,负责接收输入 x,并将输入通过函数 h 变换为信号 y:
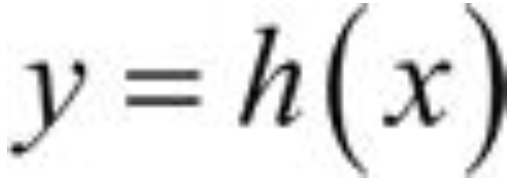
第二个网络将编码的信号 y 作为其输入,通过函数f得到重构的信号 r:
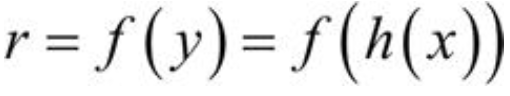
定义误差 e 为原始输入 x 与重构信号 r 之差,e=x–r,网络训练的目标是减少均方误差(MSE),同 MLP 一样,误差被反向传播回隐藏层。
5.总结
自编码器(autoencoder)是神经网络的一种,经过训练后能尝试将输入复制到输出。自编码器(autoencoder)内部有一个隐藏层 y,可以产生编码(code)表示输入。该网络可以看作由两部分组成:一个由函数 y =h(x) 表示的编码器和一个生成重构的解码器 r = f(y)。如果一个自编码器只是简单地学会将处处设置为 f(h(x)) = r,那么这个自编码器就没什么特别的用处。相反,我们不应该将自编码器设计成输入到输出完全相等。这通常需要向自编码器强加一些约束,使它只能近似地复制,并只能复制与训练数据相似的输入。这些约束强制模型考虑输入数据的哪些部分需要被优先复制,因此它往往能学习到数据的有用特性。
二.VAE变分自编码器
1.AE和VAE
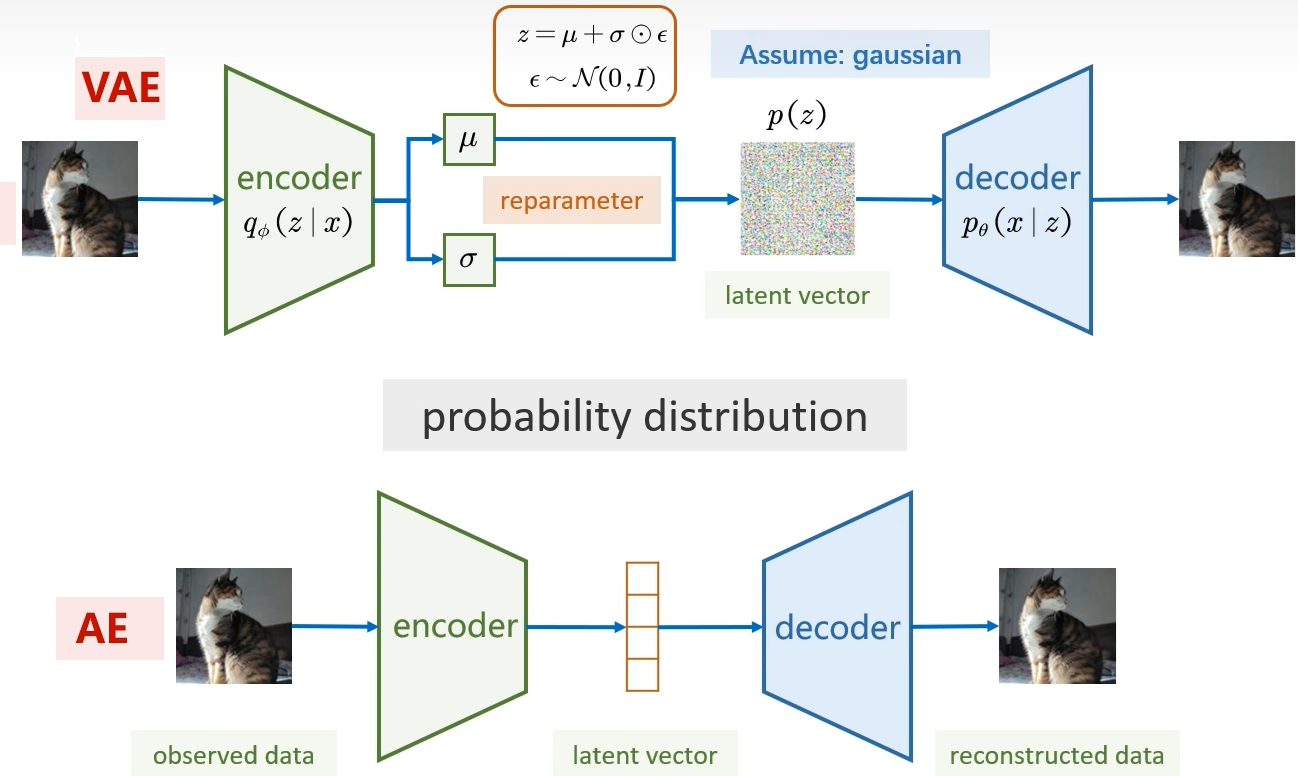
(1)下方:AE(自编码器)
这是 VAE 的 “前身”,流程是 **“输 入→编码→解码→重构” 的确定性流程 **:
- Observed data(观测数据):输入原始数据(比如图中的猫图片)。
- Encoder(编码器):将输入数据直接压缩成一个固定的隐向量(latent vector)(图中橙色方块)。
- 这里的隐向量是 “确定性” 的:同一输入会得到完全相同的隐向量。
- Decoder(解码器):将固定的隐向量还原成与输入维度相同的输出(Reconstructed data,重构数据)。
- 核心特点:
- 只能做 “重构”(让输出尽量和输入一样),但隐向量没有规律(不同输入的隐向量分布混乱),无法生成新样本(随机选一个隐向量,解码后可能是无意义的内容)。
(2)上方:VAE(变分自编码器)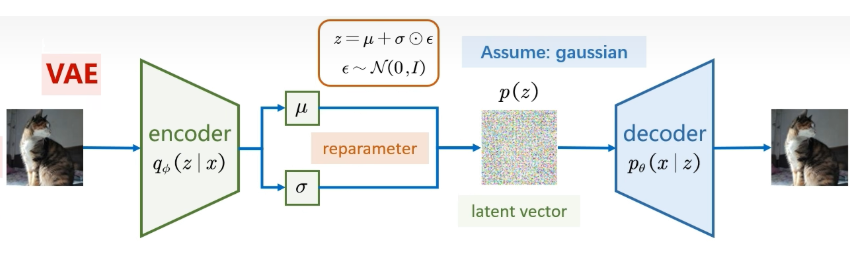
VAE 在 AE 基础上加入了概率分布约束,流程是 **“输入→编码出分布→采样隐向量→解码→重构” 的概率流程 **:
- Observed data(观测数据):同样是输入原始数据(猫图片)。
- Encoder(编码器):不是输出 “固定隐向量”,而是输出隐向量的概率分布参数:
μ(均值)和σ(标准差),对应图中绿色方框的两个输出。- 这里的编码器用
q_φ(z|x)表示:“在给定输入 x 的情况下,隐向量 z 服从的分布(由参数 φ 控制)”。
- Reparameter(重参数化):这是 VAE 的核心技巧(解决采样不可导的问题):
- 先从标准高斯分布 N (0,I) 中采样一个噪声
ε(图中橙色框的公式)。 - 再通过
z = μ + σ ⊙ ε计算隐向量 z(⊙是逐元素相乘)。 - 这样得到的 z 既服从 “以 μ 为均值、σ² 为方差” 的高斯分布,又能让梯度回传到编码器。
- 先从标准高斯分布 N (0,I) 中采样一个噪声
- Latent vector(隐向量):VAE 的隐向量是概率化的(图中彩色方块),服从预设的先验分布
p(z)(图中 “Assume: gaussian” 表示假设先验分布是高斯分布)。 - Decoder(解码器):用
p_θ(x|z)表示:“在给定隐向量 z 的情况下,输出 x 服从的分布(由参数 θ 控制)”,最终解码出重构数据。 - 核心特点:
- 隐向量 z 的分布是连续、有规律的,因此可以随机采样 z 生成全新样本(比如随机生成不同的猫图片)。
(3)变分自编码器做出的改变
那么变分自编码器(VAE)和自编码器差别在哪里呢?我认为最大的改变就是潜在表示。在自编码器中,潜在表示是一个固定值,而 VAE 中,潜在表示则是一个不确定变量,或者换一个说法,是一个概率分布。
在 VAE 中,编码器不再只学习提取输入数据的编码信息,而是去学习获取输入数据的概率分布。在原始论文中,我们设定这一概率分布为正态分布,模型也就变成了这样:
-
与此同时,中间量我们不再叫潜在变量,而是称为潜在空间(也称潜在分布,隐变量等),并使用 Z 来表示,用来凸显其是一个变化的量。
-
解码器要做的工作就是如何从这样的概率分布中采样并还原成最终的输出。
三.VAE过程讲解
针对1(2)的VAE大致过程展开细节说明
- Observed data(观测数据):同样是输入原始数据(猫图片)。
- Encoder(编码器):不是输出 “固定隐向量”,而是输出隐向量的概率分布参数:
μ(均值)和σ(标准差),对应图中绿色方框的两个输出。- 这里的编码器用
q_φ(z|x)表示:“在给定输入 x 的情况下,隐向量 z 服从的分布(由参数 φ 控制)”。
输入图像没什么好说的,直接从Encoder部分说起
1.Encoder部分
(1)怎么输出均值 μ 和方差(或 logσ²)这两个参数?
这是 ** 神经网络的 “拟合能力”** 在起作用 —— 编码器是个 “专门设计的神经网络”,最后一层输出拆成两部分,直接得到这两个参数。即编码器本质是一个神经网络(比如卷积网络),它的 “输出层设计” 决定了会输出这两个参数:
举个具体例子(以 MNIST 手写数字为例):
- 原始输入是 28×28 的图片(784 维);
- 编码器是一个卷积神经网络(或全连接网络),中间经过几层特征提取后,最后一层的输出维度是 “2× 隐向量维度”(比如隐向量是 32 维,输出层就是 64 维);
- 把这 64 维的输出 “拆成两部分”:前 32 维是均值 μ,后 32 维是方差的对数 logσ²(或直接是方差 σ²)。
简单说:编码器是一个 “定制输出的神经网络”,它通过训练,学会了 “看一张图,就输出这张图对应的隐空间分布的 μ 和 logσ²”。
(2)再使用μ 和 logσ²得到概率分布
原始图像和分布有什么关系?怎么从原始图像得到分布?
原始图像和这个分布的关系是:这个分布代表 “这张图像对应的隐向量应该服从的概率规律”——
比如输入一张手写 “5” 的图:
- 编码器会输出 μ(代表 “标准 5 的隐向量”)和 logσ²(代表 “5 的隐向量可以波动的范围”);
- 先把 logσ² 转成方差 σ²:因为 logσ² 是方差的对数,所以 σ² = exp (logσ²)(取指数)
- 对应的分布就是 “以 μ 为中心、σ² 为波动范围的高斯分布”,这个分布里的所有隐向量,都对应 “和这张图相似的 5”(比如胖一点的 5、瘦一点的 5)。
而 “从原始图像得到分布” 的过程,是训练让神经网络 “记住了图像和分布的对应关系”:训练时,模型会不断调整编码器的参数,让 “这张图对应的 μ 和 σ²” 满足两个目标:
- 用这个分布采样出的隐向量,能让解码器重构出和原图相似的结果(保证分布对应 “这张图的特征”);
- 这个分布尽量接近预设的先验分布(比如标准高斯分布,保证分布在隐空间里是规律的)。
训练完成后,编码器就 “学会了”:看到某张图,就输出这张图对应的 “合理分布参数”。
(3)高维概率分布的理解
多维高斯分布可以拆成每个维度独立的一维高斯分布来理解:
- 比如 隐向量z 是 32 维,那么 z 的第 1 维服从 “均值 μ₁、方差 σ₁²” 的一维高斯分布,第 2 维服从 “均值 μ₂、方差 σ₂²” 的一维高斯分布…… 以此类推;
- “以 μ 为中心” 是指:z 的每个维度的数值,大部分集中在对应的 μᵢ附近;
- “σ² 为波动范围” 是指:z 的每个维度的数值,会在 μᵢ±σᵢ的范围内波动(σ 是标准差,σ² 是方差)。
2.重参数化部分
3.Reparameter(重参数化):这是 VAE 的核心技巧(解决采样不可导的问题):
- 先从标准高斯分布 N (0,I) 中采样一个噪声
ε(图中橙色框的公式)。- 再通过
z = μ + σ ⊙ ε计算隐向量 z(⊙是逐元素相乘)。- 这样得到的 z 既服从 “以 μ 为均值、σ² 为方差” 的高斯分布,又能让梯度回传到编码器。
(1)重参数化过程
- 重参数化核心是生成隐向量 z:
- 重参数化采样:从标准高斯分布 N (0,1) 中采样一个和 z 维度相同的 ε(采样 ε 的过程,就是给 ε 的每个维度,都从标准高斯分布(N (0,1))里单独随机取一个值,最终得到和隐向量 z 维度相同的 ε 向量。),然后用公式
z = μ + ε × sqrt(σ²)(sqrt 是开平方,得到标准差 σ)计算出隐向量 z。 - 得到 z 之后,就可以输入解码器,生成新的图像(或重构原始图像)。
(2)回忆标准高斯分布
标准高斯分布(标准正态分布)是均值为0、标准差为1的高斯分布,记作X~N(0,1)。其概率密度函数为:
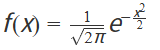
该分布具有对称性,约68.27%的数据落在[-1,1]区间,95.45%落在[-2,2],99.73%落在[-3,3]。
3.Decoder部分
Decoder(解码器):用
p_θ(x|z)表示:“在给定隐向量 z 的情况下,输出 x 服从的分布(由参数 θ 控制)”,最终解码出重构数据。
(1)解码器过程
解码器是一个 **“升维 + 特征还原” 的神经网络 **,核心是把 “低维隐向量” 还原成 “高维图像”,以 MNIST 手写数字(隐向量 32 维→图像 28×28=784 维)为例:
- 升维:先用全连接层把 32 维的隐向量,“放大” 成更高维度的向量(比如 32 维→256 维→784 维);
- 或者用转置卷积层(如果是图像任务):把低维的隐向量先转成 “小尺寸、高通道” 的特征图(比如 32 维→4×4×64 的特征图),再通过转置卷积逐步把尺寸放大到 28×28。
- 还原图像:最后一层用激活函数(比如 sigmoid)把输出值压缩到 0~1 之间,对应图像的像素亮度,最终得到 28×28 的图像。
4.具体例子
举个具体的数值例子(以 32 维隐向量为例),这是已经训练好后的VAE生成过程,不提训练过程:
- 假设编码器输出:
- μ 是 32 维向量:
[1.2, 0.5, -0.3, ..., 0.8](共 32 个数值); - logσ² 是 32 维向量:
[0.1, 0.2, 0.15, ..., 0.25];
- μ 是 32 维向量:
- 计算 σ²:对 logσ² 取指数,得到
[exp(0.1)=1.105, exp(0.2)=1.221, ...]; - 采样 ε:从标准高斯分布生成 32 维向量,比如
[0.3, -0.2, 0.5, ..., 0.1]; - 计算 z:逐维度计算
z_i = μ_i + ε_i × sqrt(σ²_i),得到 32 维的 z; - 解码 z:把 z 输入解码器,解码器通过神经网络把 32 维→784 维(28×28),输出一张新的手写数字图片。
四.VAE训练过程
我上面的讲的例子是 VAE训练好之后的生成过程(用训练好的编码器输出 μ/σ²、采样 z、解码生成图片),而 ELBO 是训练编码器和解码器时的 “优化目标”—— 它决定了 “编码器输出的 μ/σ² 是否合理”“解码器生成的图片是否足够像原始输入”。这里我还不想详细解释,只是过一遍训练流程,看看ELBO是在哪,ELBO详尽学习后面再说
整个流程举例:
假设我们要训练一个生成 MNIST 手写数字的 VAE,隐向量维度设为 32。
步骤 1:准备数据
- 加载 MNIST 数据集(手写数字图片,28×28 像素,标签是 0-9);
- 把图片转成张量(维度:
[批量大小, 1, 28, 28]),并归一化到 0~1 之间。
步骤 2:定义 VAE 模型(编码器 + 解码器)
- 编码器:
- 结构:卷积层(提取图像特征)→ 全连接层(输出
2×32=64维); - 功能:输入图片,输出 32 维的均值 μ和 32 维的log 方差 logσ²。
- 结构:卷积层(提取图像特征)→ 全连接层(输出
- 解码器:
- 结构:全连接层(把 32 维隐向量升维)→ 转置卷积层(放大尺寸);
- 功能:输入隐向量 z,输出 28×28 的重构图片。
步骤 3:初始化训练组件
- 优化器:选择 Adam(常用优化器,适合神经网络训练);
- 损失函数:用 “重构损失(BCELoss,交叉熵) + KL 散度损失”(对应 ELBO 的负数),在这里使用ELBO。
步骤 4:批量训练(核心循环)
对每一批数据,执行以下操作:
- 输入图片:取一批 MNIST 图片(比如批量大小 = 64,维度
[64, 1, 28, 28]); - 编码:得到 μ 和 logσ²:
- 把图片输入编码器,输出 64 维向量,拆分成 32 维 μ 和 32 维 logσ²;
- 重参数化:生成隐向量 z:
- 采样 ε:从标准高斯分布 N (0,1) 生成 32 维向量(批量大小 = 64,所以维度
[64, 32]); - 计算 z:
z = μ + ε × torch.exp(0.5 × logσ²)(exp(0.5×logσ²)是标准差 σ);
- 采样 ε:从标准高斯分布 N (0,1) 生成 32 维向量(批量大小 = 64,所以维度
- 解码:生成重构图片:
- 把 z 输入解码器,输出 64 张 28×28 的重构图片;
- 计算损失:
- 重构损失:计算 “重构图片” 和 “原始图片” 的 BCELoss;
- KL 散度损失:计算
-0.5 × torch.sum(1 + logσ² - μ² - torch.exp(logσ²)); - 总损失:重构损失 + KL 散度损失;
- 反向传播 + 更新参数:
- 清空优化器的梯度;
- 损失反向传播(计算编码器和解码器的参数梯度);
- 优化器更新参数(调整编码器和解码器的权重)。
步骤 5:迭代训练
重复 “步骤 4”,遍历整个 MNIST 数据集(这叫 1 个 Epoch),通常训练 10~50 个 Epoch:
- 每训练几个 Epoch,查看损失是否逐渐下降;
- 同时可以随机采样 z,输入解码器生成图片,观察生成效果是否越来越清晰。
步骤 6:训练完成
当损失稳定、生成的图片足够清晰时,停止训练:
- 保存编码器和解码器的参数;
- 后续可以用 “采样 z→输入解码器” 的方式,生成新的手写数字。
五.CVAE
1.CVAE 完整流程拆解(以 “生成指定品种的猫图片” 为例)
(1) Observed data(观测数据)+ Condition(条件变量):双输入组合
- 观测数据 x:原始数据(如任意猫图片,和 VAE 的输入一致)。
- 条件变量 c:额外的约束信息(如 “布偶猫”“橘猫” 的品种标签、“黑色” 的颜色属性,或 “幼猫” 的年龄特征)。
- 核心不同:VAE 仅输入 x,CVAE 必须同时输入 “x + c”,条件 c 是全程贯穿的核心约束。
(2) Encoder(编码器):基于 “x+c” 输出隐分布参数
- 编码器用 q_φ(z|x,c) 表示:“在同时给定输入 x 和条件 c 的情况下,隐向量 z 服从的分布(由参数 φ 控制)”。
- 输出:和 VAE 一样,输出隐向量 z 的概率分布参数 —— 均值 μ 和标准差 σ(绿色方框双输出)。
- 核心不同:VAE 的编码器只依赖 x 计算 μ 和 σ,CVAE 的编码器会融合 x 和 c 的信息(比如 “布偶猫图片 + 布偶标签” 共同决定 z 的分布),确保 z 和条件 c 强关联。
(3) Reparameter(重参数化):逻辑不变,z 的分布受 c 约束
- 流程和 VAE 完全一致:先从标准高斯分布 N (0,I) 采样噪声 ε,再通过 z = μ + σ ⊙ ε 计算隐向量 z(⊙为逐元素相乘)。
- 核心不同:VAE 的 z 服从 “全局统一的先验分布 p (z)”,而 CVAE 的 z 服从 “基于条件 c 的先验分布 p (z|c)”(比如 “布偶猫” 对应隐空间的一个子区域,“橘猫” 对应另一个子区域)。z 的分布被 c 限定在特定范围,保证后续生成符合条件。
(4) Latent vector(隐向量):条件化的概率隐向量
- 隐向量 z 依然是概率化的(彩色方块),但分布被条件 c 约束:不同的 c 会对应隐空间中不同的 “子分布”。
- 核心不同:VAE 的隐空间(所有可能的隐向量组成的集合)是全局共享的(所有猫图片的 z 混在一起),CVAE 的隐空间按 c 划分(每类条件对应一个子空间),比如 “布偶猫的 z” 和 “橘猫的 z” 不会重叠。
(5) Decoder(解码器):基于 “z+c” 重构 / 生成数据
- 解码器用 p_θ(x|z,c) 表示:“在同时给定隐向量 z 和条件 c 的情况下,输出 x 服从的分布(由参数 θ 控制)”。
- 输出:解码后得到 “符合条件 c 的重构数据 x̂”(比如输入 “任意猫图片 + 布偶标签”,重构出 “布偶猫风格的该图片”);生成新样本时,也需结合 z 和 c 输出(比如 “布偶猫的 z + 布偶标签” 生成全新布偶猫图片)。
- 核心不同:VAE 的解码器仅依赖 z 生成 x,CVAE 的解码器必须同时输入 z 和 c——c 会强制解码器输出符合约束的结果,避免 “生成布偶猫标签却产出橘猫图片”。
2.以MNIST为例举例说明条件c
以 “用 CVAE 生成指定数字的手写体(MNIST 数据集)” 为例,条件变量 c 是 “0-9” 的离散标签(经独热编码转多维向量),拆解 CVAE 的完整工作流程,看一下什么是具体的“条件c”:
(0)示例背景
目标:输入 “数字标签 c”,CVAE 能定向生成对应数字的手写图片(比如输入 c=3,生成手写体 “3”;输入 c=7,生成手写体 “7”,这就以c=3为例说明)。
- 观测数据 x:MNIST 数据集中的手写数字图片(28×28 像素,单通道灰度图)。
- 条件变量 c:数字标签 “0-9”(离散型),经独热编码转为 10 维向量(比如 c=3→[0,0,0,1,0,0,0,0,0,0],c=7→[0,0,0,0,0,0,0,1,0,0])。
- 模型核心:通过 “x+c” 双输入训练,让模型学会 “给定 c 时,x 的概率分布”( c=3 对应所有手写 “3” 的图片分布)。
CVAE 具体工作步骤(训练 + 生成):
(1)第一步:数据预处理(关键是 c 的编码)
- 对观测数据 x:将每张 28×28 图片展平为 784 维向量(或保留二维结构用卷积处理),归一化到 [0,1] 区间。
- 对条件变量 c:给每个数字标签做独热编码 ——10 个类别对应 10 维向量,只有对应数字的位置为 1,其余为 0( c=3→[0,0,1,0,0,0,0,0,0,0])。
- 最终训练数据对:(x, c) =(784 维图片向量,10 维独热编码标签),(手写 “3” 的图片向量,[0,0,0,1,0,0,0,0,0,0])。
第二步:训练阶段(编码器 + 重参数化 + 解码器)
(2)编码器:输入 “x+c”,输出隐分布参数
- 编码器结构:用全连接层或卷积层搭建,输入是 “x(784 维)和 c(10 维)拼接后的向量”(总维度 784+10=794 维)。
- 核心逻辑:编码器融合 “图片特征” 和 “数字标签”,学习 q_φ(z|x,c)—— 即 “给定这张图片 x 和标签 c,隐向量 z 服从的高斯分布”。
- 输出:隐向量 z 的均值 μ(比如 20 维)和标准差 σ(20 维),维度远低于输入,实现特征压缩。
- 举例:输入 “手写 3 的图片 x + c=3 的独热向量”,编码器输出针对 “3” 的 μ 和 σ(和输入 “手写 7 的图片 + x+c=7” 输出的 μ、σ 完全不同)。
(3)重参数化:生成带条件约束的隐向量 z
- 流程和 VAE 一致:先从标准高斯分布 N (0,I) 采样 20 维噪声 ε,再通过 z=μ+σ⊙ε 计算隐向量 z(⊙是逐元素相乘)。
- 关键差异:这里的 z 是 “条件化的隐向量”—— 因 μ 和 σ 由 “x+c” 共同决定,c=3 对应的 z 会集中在隐空间的 “3 号子区域”,c=7 对应的 z 会集中在 “7 号子区域”,不同 c 的 z 几乎不重叠。
(4)解码器:输入 “z+c”,重构 x
- 解码器结构:和编码器对称的全连接层 / 卷积层,输入是 “z(20 维)和 c(10 维)拼接后的向量”(总维度 20+10=30 维)。
- 核心逻辑:解码器接收 “条件化的 z” 和 “原始约束 c”,学习 p_θ(x|z,c)—— 即 “给定隐向量 z 和标签 c,重构出对应图片 x 的分布”,即用全连接层+激活函数把低维隐向量转成高维向量。
- 输出:784 维向量(对应重构的手写数字图片),每个元素是 [0,1] 之间的概率(表示该像素的灰度值)。
(5) 损失函数:约束模型学习 “条件分布”
- 重构损失:衡量 “解码器输出的重构图片” 和 “原始图片 x” 的差异(比如交叉熵损失),确保模型能精准还原对应数字。
- KL 散度损失:约束编码器输出的 q_φ(z|x,c),接近 “条件先验分布 p (z|c)”(比如 c=3 对应一个特定的高斯分布,c=5 对应另一个高斯分布),保证同一 c 下的 z 分布连续,生成的数字多样且稳定。
- 训练目标:最小化 “重构损失 + KL 散度损失”,让模型记住 “c 和 x 的对应关系”(比如 c=3 必须对应 “3” 的图片特征)。
(6)生成阶段(定向生成指定数字)
训练完成后,就能脱离原始图片 x,仅通过 “指定 c” 生成全新的手写数字,步骤如下:
- 选择目标条件 c:比如想生成数字 “5”,就用独热编码得到 c=[0,0,0,0,0,1,0,0,0,0]。
- 采样条件化的隐向量 z:从 “c 对应的先验分布 p (z|c)” 中,随机采样一个 20 维隐向量 z(这个 z 来自隐空间的 “5 号子区域”,天生带 “5” 的特征)。
- 解码器生成图片:将 “z + c” 输入解码器,解码器根据 c 的约束,把 z 解码为 784 维向量,再 reshape 成 28×28 的灰度图。
- 输出结果:得到一张全新的、符合 c 要求的手写数字图片(比如输入 c=5 就生成 “5”,输入 c=9 就生成 “9”,不会混淆)。
条件c(独热向量)在本例中的作用
- 定向约束:全程告诉模型 “要处理 / 生成哪个数字”,避免 VAE “随机生成 0-9” 的无控问题。
- 特征融合:编码器中 c 和 x 融合,让模型知道 “这张图片是 c 对应的数字”;解码器中 c 和 z 融合,强制输出符合 c 的结果。
- 隐空间划分:通过独热编码的 c,让隐空间按数字类别划分成 10 个独立子区域,每个子区域对应一个数字,保证生成的准确性。




















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








