排序算法详解：插入、冒泡、希尔、选择、快速与归并排序
本文详细介绍了排序算法，包括插入排序、冒泡排序、希尔排序、选择排序、快速排序和归并排序的原理、时间复杂度、空间复杂度以及稳定性。对于快速排序，还讨论了三数取中和小区间优化等优化策略。此外，还提到了计数排序和堆排序的特点。
目录
2.希尔排序时间复杂度gap=3时：O(N*log3 N) gap=2时：O(N*logN)
（1）时间复杂度（未优化是O(N²) 优化最坏情况后是O(N*logN)）
3.给出快排所有的代码：（其中主要思路有递归和非递归2种，单排有3种思路，6种写法）
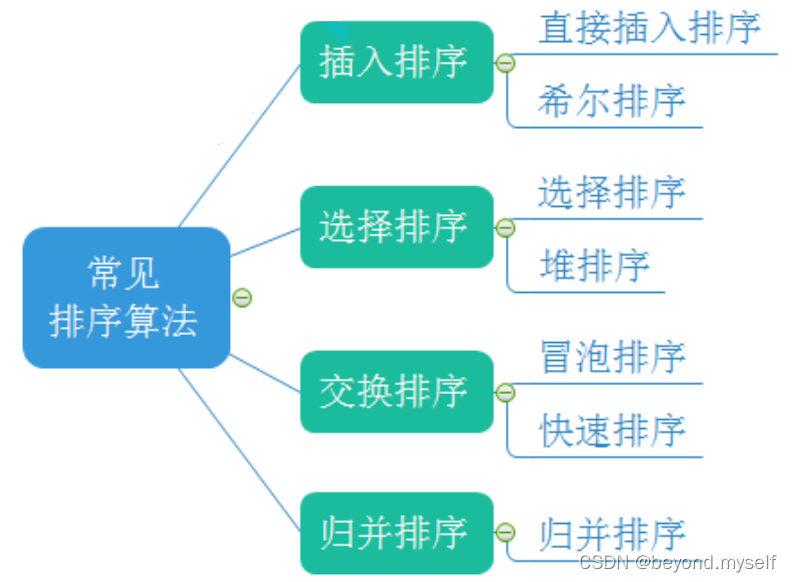
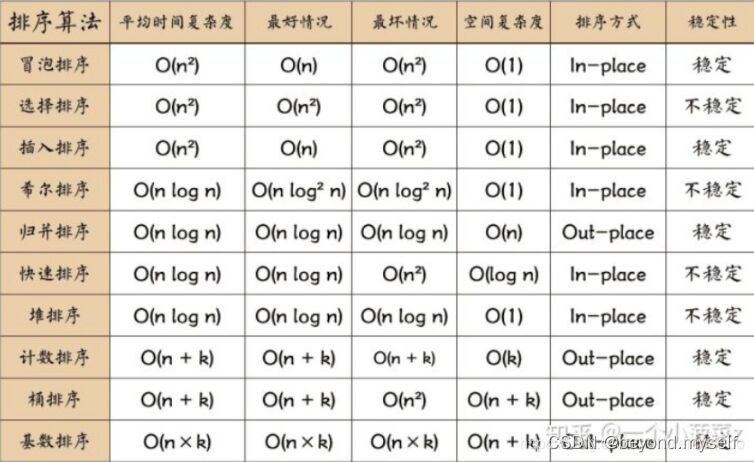
一.插入排序
1.插入排序的基本思想:
有一个有序区间，插入一个数据，依旧保持他有序
单趟排序：[0, end]有序 ，把end+1 位置的值a[end+1]插入进入，保持他依旧有序，a[end+1]和前面的有序数组从后往前比较，只要比自己大的都往后放，直到a[end]比tmp小，就跳出循环并把tmp放到这个数的后面，即：a[end + 1] = tmp;
a[end + 1] = tmp; 应写在单趟排序后面：如果将其放到 else{}里面，正常情况都能通过，但是end走到-1的特殊情况就会出问题，比如把最后一个数1插入排序，有序数组2 3 4 5 1 end=3,a[3]=5>1, end-- ；end=2, a[2]=4>1, end-- ；end=1, a[1]=3>1, end-- ；end=0, a[0]=2>1, end-- ；end=-1，此时while (end >= 0) 不满足，直接跳出循环了，最后也没有执行a[end + 1] = tmp;，即：没有把插入的值放进去。
void PrintArray(int* a, int n)
{
for (int i = 0; i < n; ++i)
{
printf("%d ", a[i]);
}
printf("\n");
}
void InsertSort(int* a, int n)
{
for (int i = 0; i < n - 1; ++i) //最后一个数下标是n-1，走到n-2位置就比较a[n-2]和a[n-1]，就比较完了，所以条件是 i < n - 1
{
int end = i;
//单趟排序：[0, end]有序 end+1位置的值，插入进入，保持他依旧有序
int tmp = a[end + 1];
while (end >= 0) //end走完整个数组就结束
{ //a[end+1]和前面的有序数组从后往前比较，只要比自己大的都往后放，
//直到a[end]比tmp小，就跳出循环并把tmp放到这个数的后面，即：a[end + 1] = tmp;
if (tmp < a[end])
{
a[end + 1] = a[end];
--end;
}
else //a[end + 1] = tmp; 如果放到 else 特殊情况不能通过,看上面解析
{
break;
}
}
a[end + 1] = tmp;
}
}
int main()
{
TestInsertSort();
return 0;
}2.插入排序的时间复杂度 O(N²)
最坏情况：逆序 O(N²)
用插入排序 排成顺序，比如5,4,3,2,1， i=0时，4和5交换，end-- 1次；数组状态：4,5,3,2,1 i=1时，end-- 2次；数组状态：3,4,5,2,1 i=2时，end-- 3次；数组状态：2,3,4,5,1 i=3时，end--4次
这些次数加起来，相当于是等差数列相加，等差数列求和：(1+n)*n/2=n/2+n²/2 ,可知时间复杂度是O(N²)
最好情况：顺序 O(N)
因为是顺序，所以每次for循环进去就会break，执行n-1次，时间复杂度就是O(N)
3.插入排序的空间复杂度 O(1)
插入排序没有开辟额外数组，只是函数调用中存储了一些局部变量，是常数个，所以空间复杂度是O(1) .
稳定性概念！！！：
4.插入排序的稳定性——稳定
插入排序思想是把end+1 位置的值a[end+1]插入进入有序数组 [0, end] 中，（假设排升序）a[end+1]从前往后逐一和有序数组 [0, end] 中的数比较，a[end+1]比这个数小，就把这个数往后挪一格，a[end+1]比这个数大，就把a[end+1]放到这个数的后面，如果a[end+1]和这个数一样，也就把a[end+1]放到这个数的后面，不会改变前后顺序，所以插入排序是稳定的。
（温馨提示：但是有的同学说，那我就让它相等时也往后挪不就改变顺序了吗？——这样确实会改变顺序了，但是如果这样说所以的排序都可以变的不稳定，所以我们规定：只要这个排序能变的稳定，那他就是稳定排序）
二.冒泡排序
1.冒泡排序思想：
单趟就是从第一个数开始，把相邻两个数逐次比较，如果前面的数大，就交换这两个数，这一趟下来一定把最大的数放到了最后面，第1趟执行单趟需要拿第一个数和后面的n-1个数逐次比较n-1次，第2趟比n-2……，第n-1趟比较1次（趟数+比较次数=n），需要执行n-1次，比较次数需要加入一个不断增长的值，正好用趟数 i ，因此先写成n-i，i是从0开始，所以要多减1，比较次数写成n-i-1（就是for (j = 0; j < n - i - 1; j++)），第n-1趟是比较1次，第n趟就是比较0次，因此我们就走n趟（就是for (int i = 0; i < n; ++i) ）只不过第n趟不比较
优化：
①如果恰好是顺序，那还是比较n²次就很浪费时间，所以加入exchange，只要交换一次就把exchange置为1，如果第一趟进去，发现一次也没交换，那exchange还是0，就是顺序，第一趟跑完后直接break，这种情况时间复杂度直接优化到了O(N)，就防止了顺序还要跑n²次的情况。
②其次，只要有序了就不会进行后面的排序：这是exchange定义进第一层循环内的目的，详细讲解：每次进行一趟排序后，发生了交换，exchange变成1，再进行下一趟时，把exchange重置成0，如果这一趟结束exchange如果依然是0，说明在这一趟之前就已经有序了，直接break即可。
void PrintArray(int* a, int n)
{
for (int i = 0; i < n; ++i)
{
printf("%d ", a[i]);
}
printf("\n");
}
// 时间复杂度:O（N^2）
// 最好情况：顺序有序 O(N)
void BubbleSort(int* a,int n )
{
int i = 0;
int j = 0;
for (i = 0; i < n; i++)
{
int exchange = 0;
for (j = 0; j < n - i - 1; j++)
{
if (a[j + 1] < a[j])
{
exchange = 1;
int tmp = a[j];
a[j] = a[j + 1];
a[j + 1] = tmp;
}
}
if (exchange == 0)
break;
}
}
void TestBubbleSort()
{
int a[] = { 9, 1, 2, 5, 7, 4, 8, 6, 3, 5 };
BubbleSort(a, sizeof(a) / sizeof(int));
PrintArray(a, sizeof(a) / sizeof(int));
}
int main()
{
TestBubbleSort();
return 0;
}2.冒泡排序时间复杂度O(N²)：
最坏情况：逆序 次次都要比较，第1趟比较n-1次，第2趟比n-2次……，第n-1趟比较1次，1+2+3+……+n-1还是等差数列求和，所以时间复杂度是O(N²)
最好情况：顺序 刚刚算过，是O(N)
3.冒泡排序空间复杂度O(1)：
冒泡并没有开额外数组，只需要存储局部变量即可，所以空间复杂度是O(1).
4.冒泡排序的稳定性——稳定
每一趟冒泡都是比较，(假设排升序)前大于后就交换两个数，如果前小于后就不交换，如果相等也不交换，所以冒泡是稳定的。
5.比较插入与冒泡排序
看似插入和冒泡最好情况都是O(N)，最坏情况都是O(N²)，但实际上他俩的效率还是有差别的：
举个例子：数组：1 2 3 4 5 6 8 7 这个数组
用插入排序运行几次？：end=0时，1<2,不用换，比较1次；end=1时，2<3,不用换，比较1次；end=2时，3<4,不用换，比较1次；end=3时，4<5,不用换，比较1次；end=4时，5<6,不用换，比较1次；end=5时，6<8,不用换，比较1次；end=6时，8>7,用换，比较1次后，8放到7的位置，7和6再比较一次，7>6,并把7放在6后面就结束。一共比较了8次。
用冒泡排序运行几次？：1和2比较，1<2，不用换，比较一次；2和3比较，2<3，不用换，比较一次；3和4比较，3<4，不用换，比较一次；4和5比较，4<5，不用换，比较一次；5和6比较，5<6，不用换，比较一次；6和8比较，6<8，不用换，比较一次；8和7比较，8>7，用换，比较一次后，交换8和7；一共比较了7次，此时数组是：1 2 3 4 5 6 8 7 ，因为已经发生过交换，exchange=1，则不结束，需要进行第二次比较：1,2比，不换；2,3比，3,4比，4,5比，5,6比，6,7比，都不换，发现exchange=0，break结束冒泡。一共比较了7+6=13次。
这个例子冒泡比插入多走了5次！由此我们发现：如果是顺序有序，那么插入和冒泡是一样的
但是如果是局部有序或者接近有序,那么插入适应性更好，比较次数更少。（比如一个数组整体顺序是乱的，但中间有一段是顺序，也会减少一些比较次数）
总体来说是一个数量级，但是局部有序情况插入还是比冒泡强
三.希尔排序
代码先给出来，我们逐步讲解：
void ShellSort(int* a, int n)
{
int gap = n;
while (gap > 1)
{
gap = gap / 3 + 1;
for (int i = 0; i < n - gap; i++)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}
void TestShellSort()
{
int a[] = { 9, 1, 2, 5, 7, 4, 8, 6, 3, 5 };
ShellSort(a, sizeof(a) / sizeof(int));
PrintArray(a, sizeof(a) / sizeof(int));
}
int main()
{
TestShellSort();
return 0;
}1.希尔排序的思想：
相当于插入排序的优化；我们知道插入排序在 局部有序或者接近有序 的情况下适应性更强，比较次数更少，那我们就想怎么快速把它排成接近有序的数组呢？——进行预排序
（1）预排序（目的使数组接近有序）：
方法一(传统法)：分组后每一组进行插入排序，分组排大的数更快的到后面小的数更快的到前面接近有序，给数组 9, 1, 2, 5, 7, 4, 8, 6, 3, 5 ，我们可以给出一个gap（假设gap=3），从下标0开始把隔着gap距离的数先进行插入排序，从下标1开始把隔着gap距离的数先进行插入排序，从下标2开始把隔着gap距离的数先进行插入排序，一共gap组，每一组走到下标n-1-gap就结束插入排序， 这样间距是gap的数就是有序的，虽然整体不是有序但是接近有序。（分成gap=3组插入排序）
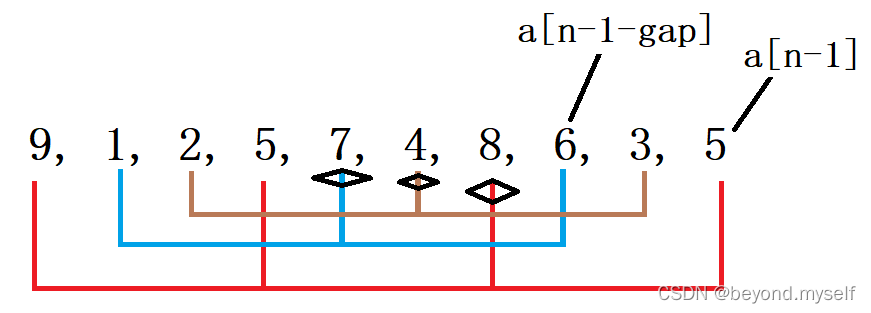
举例说明：数组：9, 1, 2, 5, 7, 4, 8, 6, 3, 5，gap=3
先从下标0开始把隔着gap=3距离的数进行插入排序后就是：5, 1, 2, 5, 7, 4, 8, 6, 3, 9。
数组状态：5, 1, 2, 5, 7, 4, 8, 6, 3, 9
再从下标1开始把隔着gap=3距离的数进行插入排序后就是：5, 1, 2, 5, 6, 4, 8, 7, 3, 9
数组状态：5, 1, 2, 5, 6, 4, 8, 7, 3, 9
再从下标2开始把隔着gap=3距离的数进行插入排序后就是：5, 1, 2, 5, 6, 3, 8, 7, 4, 9
进行gap=3次就变得整体接近有序了，这样怎么实现呢？我们先把插入排序的间距1改成gap，再让每组完整的插入排序从下标0,1,2分别进行gap=3次，每一组走到下标n-1-gap就结束插入排序
int gap = 3;
for (int j = 0; j < gap; j++) //分成gap组
{
for (int i = j; i < n - gap; i += gap) //每组完整的插入排序
{
int end = i; //到下标为i数据的单次插入排序
int tmp = a[end + gap];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}上面我们说要分别从下标0，下标1，下标2开始把间距为gap的一串数进行插入排序，这样需要两层排序，写全要3层循环，但是最优的方法一层循环即可
方法二：，把 i += gap 改成 i++ ，不分组了，过程请看动态图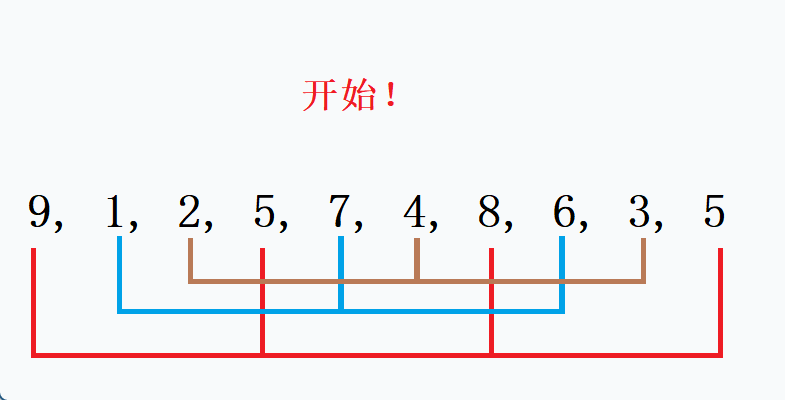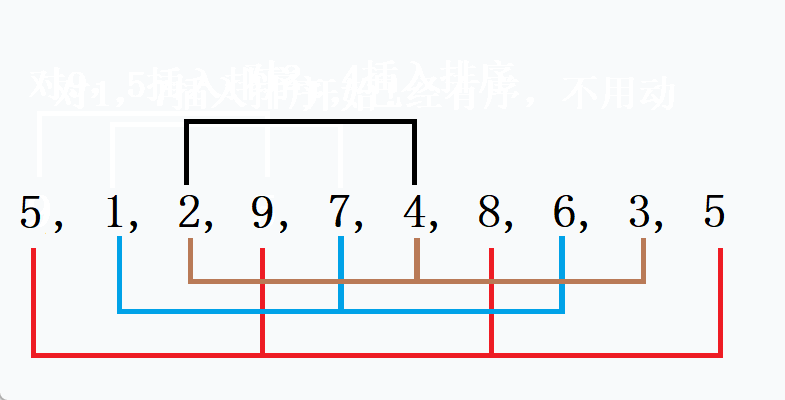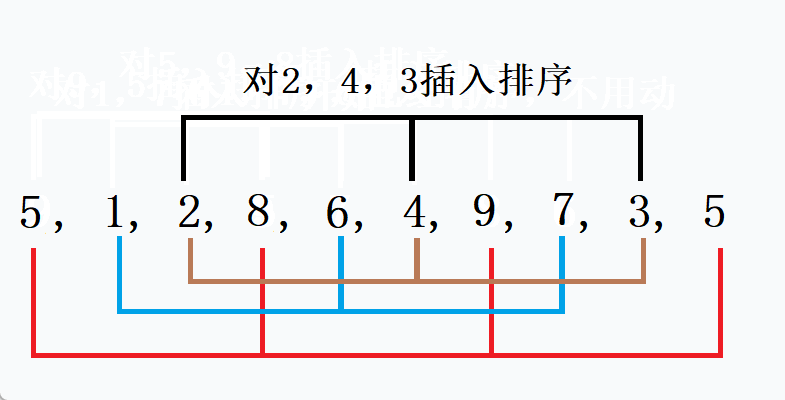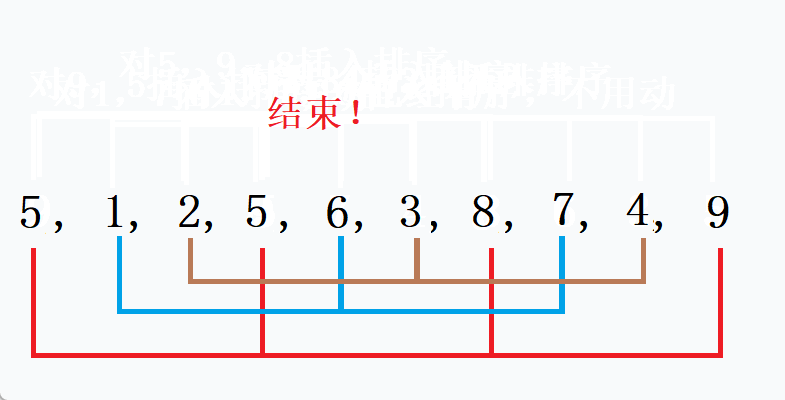
如果gap越小,越接近有序
gap越大的，大的数据可以更快到最后，小的数可以更快到前面，但是它越不接近有序
（2）最后再直接插入排序
1、gap > 1 预排序
2、gap == 1 直接插入排序
加一层循环，对gap进行控制，通常gap从n/3开始依次缩小，每循环一次gap就/3,gap越小，越接近有序，最后要进行一次插入排序，即：gap=1，但是如果只是每次gap=gap/3，最后有可能不是1，假如gap=8,8/3=2,2/3=0,所以为了最后进行一次插入排序，写成gap=gap/3+1，这样gap最后一次一定是1，并且条件写成while (gap > 1)，使gap=1插入排序以后就结束。
void ShellSort(int* a, int n)
{
int gap = n;
while (gap > 1)
{
gap = gap / 3 + 1;
for (int i = 0; i < n - gap; i++)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}2.希尔排序时间复杂度gap=3时：O(N*log3 N) gap=2时：O(N*logN)
（1）先看内存for循环的复杂度：有两种情况
①预排序gap很大时，数据跳的很快，差不多是O(N)，假设gap=n/3（n是数组长度），for循环要走n-gap=2n/3 次，如果数组前面有一个很大的数，他要跳到最后一个，也最多需要3次，就是每次end增加后进去最多也就跳3次，3*（2n/3）=2n，所以时间复杂度是O(N)
②gap很小时,他很接近有序差不多也是O(N)，因为gap在很大的时候（gap>1时，预排序的情况）进行预排序以后数组已经接近有序了，当gap每次/3+1到gap=1时，就是插入排序一个接近有序的数组，是插入排序的最好情况（或者其他gap比较小的时候，也是很接近有序），时间复杂度也是O(N)
所以不管gap很大还是很小的时候数据复杂度都是O(N)。
（2）外层
int gap = n;
while (gap > 1)
{
gap = gap / 3 + 1;
+1太小忽略的就行，意思就是：n/3/3/3……=1，3^x=n,x=log3 N x循环次数=log以3为底N的对数，时间复杂度是：O(log3 N)
总结：内层O(N)*外层O(log3 N)=O(N*log3 N)
希尔排序时间复杂度就是O(N*log3 N) ，如果你的gap取的是2，那时间复杂度就是O(N*logN)，经计算平均下来时间复杂度为：O(N^1.25)
有文献：
3.希尔排序空间复杂度O(1)
希尔排序就是插入排序前加了个预排序，也没有开额外数组，只是放局部变量，所以空间复杂度是O(1)。
4.希尔排序的稳定性——不稳定
预排序时分组可能把相同的数分到不同的组，不同组再分别插入排序（这就是预排序），就有可能把相同的数前后顺序改变，所以希尔排序不稳定。
四.选择排序
先给出代码：
void PrintArray(int* a, int n)
{
int i = 0;
for (i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
printf("\n");
}
void swap(int* pa, int* pb)
{
int tmp = *pa;
*pa = *pb;
*pb = tmp;
}
void SelectSort(int* a, int n)
{
int left = 0;
int right = n - 1;
while (left < right) //当left和right中间没有值或只有一个值结束循环(只有一个值时说明他的左边都是比他小的值，右边都是比他大的值，并且有序)
{
int mini = left;
int maxi = left;
for (int i = left + 1; i <= right; i++) //遍历数组，找最大最小值的下标
{
if (a[i] < a[mini])
mini = i;
if (a[i] > a[maxi])
maxi = i;
}
swap(&a[left], &a[mini]); //把最小值放到左
最低0.47元/天 解锁文章
扫一扫
1165
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
