本文介绍了GraphSAGE，一种用于大规模图的归纳学习框架，解决了直推式学习无法泛化到未知节点的问题。GraphSAGE通过采样邻居节点并聚合特征，扩展了GCN以适应归纳学习任务。论文提出了平均、GCN归纳式、LSTM和Pooling等多种聚合函数，并定义了基于图的无监督损失函数。实验表明，GraphSAGE在节点分类和图分类任务上表现出色，适用于不断演化和包含未知节点的图数据集。
论文标题
Inductive Representation Learning on Large Graphs——NIPS17
论文链接
https://proceedings.neurips.cc/paper/2017/file/5dd9db5e033da9c6fb5ba83c7a7ebea9-Paper.pdf文章背景
在大规模图上学习节点embedding，在很多任务中非常有效，如学习节点拓扑结构的 DeepWalk 以及同时学习邻居特征和拓扑结构的semi-GCN。
但是现在大多数方法都是直推式（transductive）学习， 不能直接泛化到未知节点。这些方法是在一个固定的图上直接学习每个节点embedding，但是大多情况图是会演化的，当网络结构改变以及新节点的出现，直推式学习需要重新训练（复杂度高且可能会导致embedding会偏移），很难落地在需要快速生成未知节点embedding的机器学习系统上
直推式(transductive)学习：从特殊到特殊，仅考虑当前数据。在图中学习目标是直接生成当前节点的embedding，例如DeepWalk、LINE，把每个节点embedding作为参数，并通过SGD优化，又如GCN，在训练过程中使用图的拉普拉斯矩阵进行计算，
归纳(inductive)学习：平时所说的一般的机器学习任务，从特殊到一般：目标是在未知数据上也有区分性。
本文提出归纳学习—GraphSAGE(Graph SAmple and aggreGatE)
框架（核心是如何聚合节点邻居特征信息），通过训练聚合节点邻居的函数（卷积层），使GCN扩展成归纳学习任务，对未知节点起到泛化作用。
框架介绍：
1.前向传播（即生成节点的embedding）
下图是GraphSAGE 生成目标节点（红色）embededing并供下游任务预测的过程：
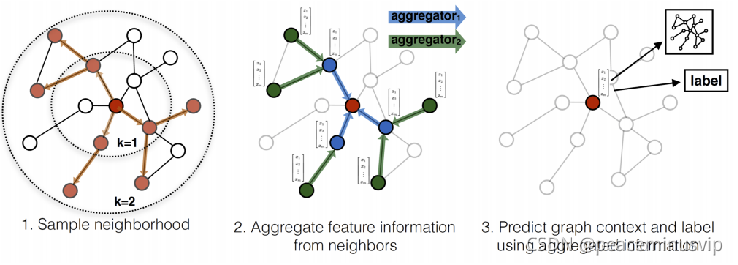
4-5行是核心代码，介绍卷积层操作：
(1)聚合与节点v相连的邻居（采样）k-1层的embedding，得到第k层邻居聚合特征
(2)与节点v第k-1层embedding 
拼接，并通过全连接层转换，得到节点v在第k层的embedding 
2.聚合函数
伪代码第4/5行可以使用不同聚合函数，本文介绍四种满足排序不变量的聚合函数：平均、GCN归纳式、LSTM、pooling聚合器。（因为邻居没有顺序，聚合函数需要满足排序不变量的特性，即输入顺序不会影响函数结果）
(1)平均聚合：先对邻居embedding每个维度取平均，然后与目标节点embedding拼接后进行非线性转换.
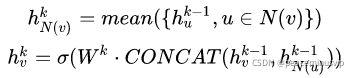
(2)GCN归纳式聚合：直接对目标节点和所有邻居emebdding中每个维度取平均（替换伪代码中第5、6行），后再非线性转换：
3. 损失设定
基于图的无监督损失：希望节点u与“邻居”v的embedding相似（对应公式第一项），而与“没有交集”的节点 不相似（对应公式第二项)。
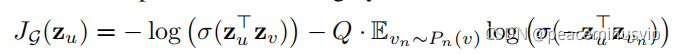
为节点u通过GraphSAGE生成的embedding。
节点v是节点u随机游走访达“邻居”。
表示负采样：节点是从节点u的负采样分布 Pn(v)采样的，Q为采样样本数。
embedding之间相似度通过向量点积计算得到
实验数据集
(1)Citation 论文引用网络（节点分类）
(2)Reddit web论坛 （节点分类）
(3)PPI 蛋白质网络 （graph分类） 实验效果
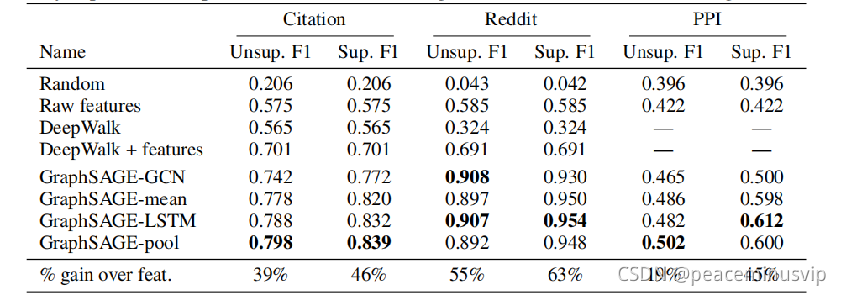
总结和思考
GCN不是归纳式，还是全局的，因为每次迭代AXW 是会用到A整个图邻接矩阵；GraphSAGE可以说对GCN做了进一步精简，每次迭代只抽样取直接相连的邻居，局部.
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
