- 一.大数据算法的难度
二.大数据求解问题的过程1.访问全部数据时间过长
--读取部分数据---------------时间亚线性算法
2.数据难于放入内存计算
--将数据存储在磁盘上--------外存算法
--仅基于少量数据进行计算---空间亚线性算法
3.单个计算机难以保存全部数据,计算需要整体数据
--并行处理--------------------并行算法(例如MapReduce,Hadoop)
4,计算机计算能力不足或知识不足
--人来帮忙--------------------众包算法
问题->可计算?->能行可计算?->算法设计与分析->用计算机语言实现算法->软件系统
三.大数据的算法设计技术
精确算法设计方法
并行算法
近似算法
随机算法
在线算法/数据流算法
外存算法
面向新型体系结构的算法
现代优化算法(模拟退火,遗传算法等)
四.算法分解之亚线性算法
(一)亚线性空间算法:亚线性含义:时间/空间/IO/通讯/能量等消耗o(输入规模)
亚线性时间算法:亚线性时间近似算法;性质检测算法
例: 输入:一组数据,大小未知
输出:这组数据的k个均匀抽样
要求:仅扫描数据一次
空间复杂性为o(k)
扫描到数据的前n个数字时(n>k),保存当前已扫描数据的k个均匀抽样
水库抽样算法:1.申请一个长度为k的数组A保存抽样
2.保存首先接收到的k个元素
3.当接收到第i个新元素t时,以k/i的概率随机替换A中的元素(即生成【1,i】间随机数j,若j=<k,则以t替换A[j])性质:该采样是均匀的(每个元素在抽样数组中的概率为k/n)且 算法空间复杂度为o(k)。
(二)亚线性时间计算算法:
例:输入:m个顶点的平面图,任意两点之间的距离存储在矩阵D中,即点i到点j的距离为Dij
输入大小是n=m^2;
最大的Dij是图的直径;
点之间的距离对称且满足三角不等式;
输出:该图的直径和距离最大的Dij
要求:运行时间为o(n)
平面图的直径近似算法:(无法在要求的时间内得到精确解,寻找近似算法)
近似算法:任意选择k=<m,选择使得Dkl最大的l,输出Dkl和(k,l)
近似比:Dij=<Dik+Dkj=<Dkl+Dkl=<2Dkl 近似比为2
(三)时间亚线性判定算法
例:输入:包含n个元素的0,1数组A
输出:A中的元素是否全是0.
要求:运行时间为o(n)
上述问题可采取抽样解决。
判定算法的定义:对于判定问题L,其查询复杂性为q(n)和近似参数e的性质测试算法是一个随机算法,其满足对于给定L的是一个实例x,最多进行q(|x|)次查询,并且满足(1)如果x在L之中,该算法以最少2/3的概率返回“是”;(2)如果x是e原理L的,该算法以最小2/3的概率返回“否”。




 本文探讨了大数据背景下算法面临的挑战,如时间、空间限制等,并介绍了针对这些挑战设计的算法技术,包括亚线性算法、并行算法及众包算法等。
本文探讨了大数据背景下算法面临的挑战,如时间、空间限制等,并介绍了针对这些挑战设计的算法技术,包括亚线性算法、并行算法及众包算法等。
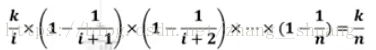
















 1337
1337

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








